7 X 2 X 7
thesills
Sep 17, 2025 · 6 min read
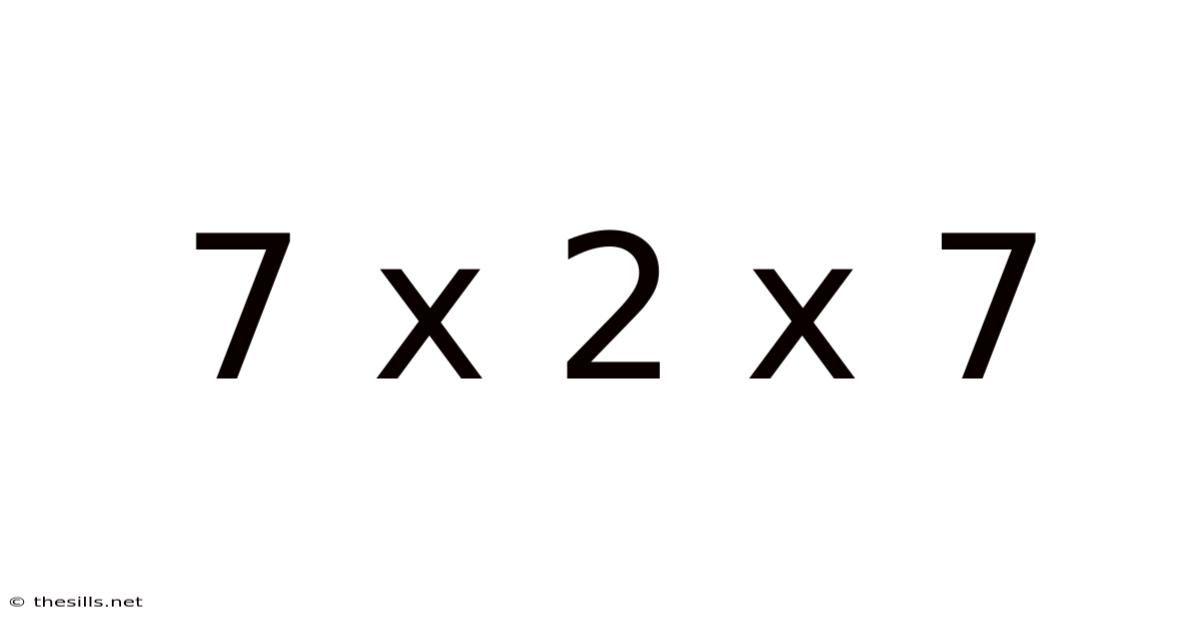
Table of Contents
Decoding 7 x 2 x 7: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple calculation of 7 x 2 x 7, moving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and connections to broader mathematical concepts. We'll delve into the intricacies of multiplication, explore different methods of solving this problem, and discuss its relevance in various fields. Understanding this seemingly basic calculation opens doors to a deeper appreciation of mathematics and its power in our world.
Introduction: The Humble Beginnings of 7 x 2 x 7
At first glance, 7 x 2 x 7 appears as a straightforward multiplication problem. The answer, 98, is easily obtained with a calculator or basic arithmetic skills. However, this seemingly simple equation serves as a gateway to explore fundamental mathematical concepts and their practical applications. This exploration will go beyond simply finding the product; we will analyze the method, the underlying principles, and the broader implications of this seemingly trivial calculation. We will explore the commutative and associative properties, the concept of prime factorization, and even touch upon the applications of multiplication in everyday life and advanced mathematical fields.
Understanding the Fundamentals: Multiplication as Repeated Addition
Multiplication is fundamentally a shorthand way of performing repeated addition. In our case, 7 x 2 x 7 can be interpreted in several ways:
-
7 x 2 x 7 = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7: This represents the repeated addition of 7, fourteen times (7 x 2 = 14, then 7 repeated 14 times). While effective for smaller numbers, this method becomes cumbersome with larger numbers.
-
(7 x 2) x 7: This illustrates the associative property of multiplication, which states that the grouping of numbers in a multiplication problem doesn't change the result. We can first multiply 7 by 2 (14) and then multiply the result by 7 (14 x 7 = 98).
-
7 x (2 x 7): This again demonstrates the associative property. We can first multiply 2 by 7 (14) and then multiply the result by 7 (7 x 14 = 98).
These different approaches highlight the flexibility and efficiency of multiplication compared to repeated addition.
The Commutative Property and its Significance
The commutative property of multiplication states that the order of the numbers doesn't affect the final product. This means that 7 x 2 x 7 is the same as 7 x 7 x 2, 2 x 7 x 7, and any other permutation of these numbers. This property is crucial in simplifying calculations and understanding the nature of multiplication. It allows us to rearrange the numbers to find the most efficient way to solve the problem, especially when dealing with larger and more complex equations.
Prime Factorization: Unpacking the Building Blocks
Prime factorization is the process of breaking down a number into its prime factors—numbers that are only divisible by 1 and themselves. Let's find the prime factorization of 98, the result of 7 x 2 x 7:
- 98 = 2 x 49
- 98 = 2 x 7 x 7
This demonstrates that 98 is composed of the prime numbers 2 and 7. Understanding the prime factorization of a number provides valuable insight into its properties and is fundamental in various mathematical fields, including cryptography and number theory.
Practical Applications: Beyond the Classroom
The seemingly simple calculation of 7 x 2 x 7 finds its application in many real-world scenarios:
-
Area Calculation: Imagine a rectangular garden with a length of 7 meters and a width of 14 meters (7 x 2). The total area would be 98 square meters (7 x 2 x 7).
-
Volume Calculation: Consider a rectangular box with dimensions 7 cm x 2 cm x 7 cm. The volume of this box would be 98 cubic centimeters.
-
Cost Calculation: If you need 7 packages of something that cost $2 each, and you need to buy 7 sets of these packages, the total cost would be $98 (7 x 2 x 7).
These are just a few examples; the principles of multiplication are ubiquitous in everyday life, from calculating costs to measuring areas and volumes.
Exploring Advanced Concepts: Number Theory and Algebra
The seemingly simple equation 7 x 2 x 7 can be a springboard for exploring more complex mathematical concepts:
-
Modular Arithmetic: In modular arithmetic, we consider the remainder after division by a specific number (the modulus). For example, 98 (mod 10) would be 8, because 98 divided by 10 leaves a remainder of 8. Modular arithmetic is used extensively in cryptography and computer science.
-
Algebraic Expressions: We can express this calculation algebraically. Let's say 'x' represents 7 and 'y' represents 2. The equation then becomes x * y * x, or x²y. This algebraic representation allows us to generalize the calculation and explore its properties in a more abstract way.
-
Sequences and Series: The number 98 could be part of a larger sequence or series. Analyzing the properties of such sequences can lead to deeper understandings of number patterns and relationships.
Different Methods of Calculation: Beyond the Standard Algorithm
While the standard multiplication algorithm is efficient, exploring alternative methods can enhance our understanding of the process:
-
Lattice Multiplication: This ancient method uses a grid to break down the multiplication into smaller, more manageable steps.
-
Distributive Property: The distributive property allows us to break down multiplication into smaller parts, making it easier to solve. For example, 7 x (2 x 7) can be expanded as (7 x 2) x 7 or 7 x (7 x 2).
-
Mental Math Techniques: With practice, many multiplication problems can be solved mentally using shortcuts and tricks.
Exploring these different methods not only helps us arrive at the answer but also provides a deeper understanding of the underlying principles of multiplication.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate 7 x 2 x 7?
- A: The easiest way depends on your preference and mathematical skills. Many find (7 x 2) x 7 or 7 x (2 x 7) to be the most straightforward approaches.
-
Q: Is there a quicker way to multiply than using the standard algorithm?
- A: Yes, there are several quicker methods, including mental math techniques, the distributive property, and lattice multiplication, all depending on the complexity of the numbers involved.
-
Q: What are some real-world examples where this calculation might be useful?
- A: Calculating areas, volumes, costs, and many other quantitative scenarios in everyday life and various professional fields make use of multiplication principles.
-
Q: How does this calculation relate to more advanced mathematical concepts?
- A: The simple calculation of 7 x 2 x 7 is a building block for understanding more complex concepts like modular arithmetic, algebraic expressions, and sequences and series.
Conclusion: The Enduring Power of a Simple Equation
While the answer to 7 x 2 x 7 is a simple 98, the journey to arrive at this answer has uncovered a wealth of mathematical principles and real-world applications. From the fundamental concepts of repeated addition and the commutative and associative properties to the more advanced concepts of prime factorization, modular arithmetic, and algebraic representation, this seemingly simple calculation has shown the interconnectedness of mathematical ideas. It emphasizes that even the most basic mathematical operations hold a profound significance, forming the foundation for more complex and sophisticated concepts, demonstrating the enduring power and elegance of mathematics. Hopefully, this exploration has not only provided a deeper understanding of the calculation itself but has also ignited a curiosity to explore the fascinating world of mathematics further.
Latest Posts
Latest Posts
-
Synopsis Of The Happy Prince
Sep 17, 2025
-
Rotational Symmetry For Isosceles Triangle
Sep 17, 2025
-
When Are Recessive Alleles Expressed
Sep 17, 2025
-
22 7 As A Decimal
Sep 17, 2025
-
300 Billion 300 Million
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 7 X 2 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.