Factorise 6x 2 5x 6
thesills
Sep 16, 2025 · 6 min read
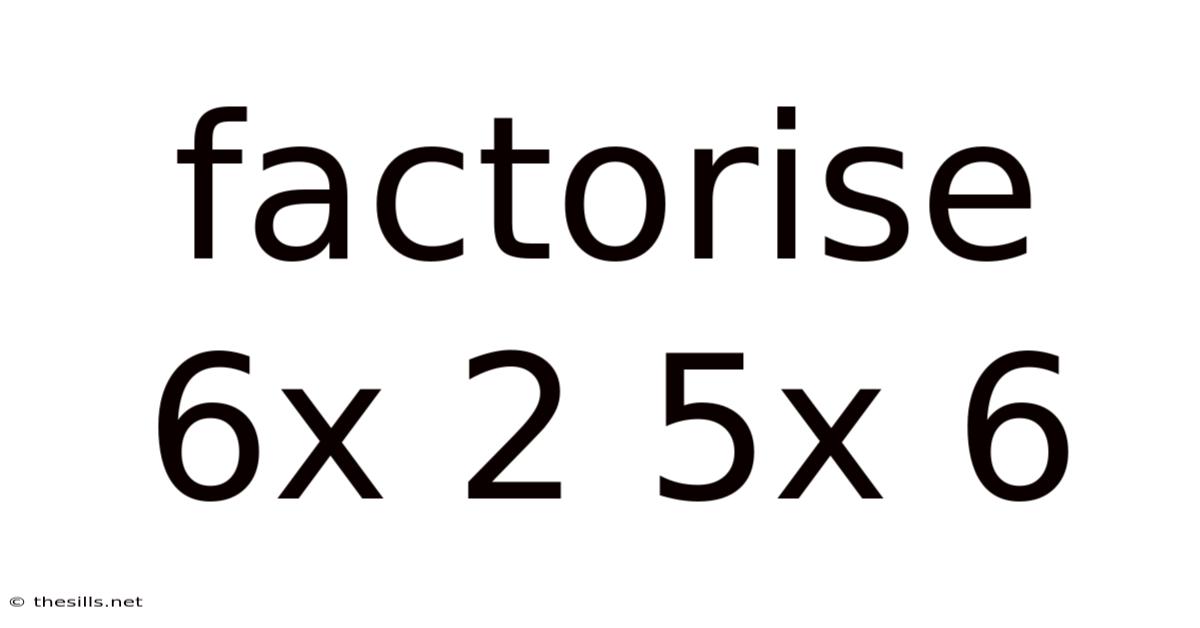
Table of Contents
Factorising 6x² + 5x - 6: A Comprehensive Guide
Factorising quadratic expressions is a fundamental skill in algebra. This article provides a detailed walkthrough of how to factorise the quadratic expression 6x² + 5x - 6, explaining the different methods and underlying principles. We'll explore several techniques, from the simple trial-and-error method to the more systematic application of the quadratic formula and completing the square. By the end, you'll not only understand how to factorise this specific expression but also gain a broader understanding of factorising quadratic equations in general. This will equip you with the skills to tackle similar problems with confidence.
Understanding Quadratic Expressions
Before diving into the factorisation of 6x² + 5x - 6, let's briefly review what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. In our example, a = 6, b = 5, and c = -6. Factorising a quadratic expression means rewriting it as a product of two linear expressions. This is crucial for solving quadratic equations and simplifying algebraic expressions.
Method 1: Trial and Error
This method involves systematically trying different combinations of factors of 'a' and 'c' until we find a pair that satisfies the middle term, 'b'.
-
Step 1: Find factors of 'a' (6): The factors of 6 are 1 and 6, and 2 and 3.
-
Step 2: Find factors of 'c' (-6): The factors of -6 are 1 and -6, -1 and 6, 2 and -3, and -2 and 3.
-
Step 3: Test combinations: We need to find a combination of factors from steps 1 and 2 that, when multiplied and added, gives us 'b' (5). Let's try some combinations:
- (2x + 1)(3x - 6): This expands to 6x² - 12x + 3x - 6 = 6x² - 9x - 6 (Incorrect)
- (2x - 1)(3x + 6): This expands to 6x² + 12x - 3x - 6 = 6x² + 9x - 6 (Incorrect)
- (2x + 3)(3x - 2): This expands to 6x² - 4x + 9x - 6 = 6x² + 5x - 6 (Correct!)
Therefore, the factorised form of 6x² + 5x - 6 is (2x + 3)(3x - 2).
Method 2: The Quadratic Formula
The quadratic formula provides a more systematic approach to finding the roots of a quadratic equation (ax² + bx + c = 0). These roots can then be used to find the factors. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
-
Step 1: Identify a, b, and c: In our expression, a = 6, b = 5, and c = -6.
-
Step 2: Substitute into the quadratic formula:
x = [-5 ± √(5² - 4 * 6 * -6)] / (2 * 6) x = [-5 ± √(25 + 144)] / 12 x = [-5 ± √169] / 12 x = [-5 ± 13] / 12
- Step 3: Solve for x:
x₁ = (-5 + 13) / 12 = 8/12 = 2/3 x₂ = (-5 - 13) / 12 = -18/12 = -3/2
-
Step 4: Convert roots to factors: The roots represent the values of x that make the expression equal to zero. To convert these roots into factors, we reverse the sign and place them in the form (x - root).
- For x₁ = 2/3, the factor is (3x - 2)
- For x₂ = -3/2, the factor is (2x + 3)
Therefore, the factorised form is (2x + 3)(3x - 2).
Method 3: Completing the Square
Completing the square is a technique used to rewrite a quadratic expression in the form (x + p)² + q. While less direct for factorisation than the previous methods, it's a valuable algebraic tool with broader applications.
- Step 1: Factor out 'a' (6):
6(x² + (5/6)x - 1)
- Step 2: Focus on the terms inside the parentheses: To complete the square, we take half of the coefficient of x (5/6), square it ((5/12)² = 25/144), and add and subtract it inside the parentheses.
6(x² + (5/6)x + 25/144 - 25/144 - 1)
- Step 3: Rewrite as a perfect square:
6((x + 5/12)² - 25/144 - 1) 6((x + 5/12)² - 169/144)
- Step 4: Factor as a difference of squares: This step utilizes the difference of squares formula: a² - b² = (a + b)(a - b). Here, a = (x + 5/12) and b = √(169/144) = 13/12.
6((x + 5/12 + 13/12)(x + 5/12 - 13/12)) 6((x + 18/12)(x - 8/12)) 6((x + 3/2)(x - 2/3))
- Step 5: Simplify:
(2x + 3)(3x -2)
Therefore, the factorised form is again (2x + 3)(3x - 2).
Choosing the Right Method
The trial-and-error method is often the quickest for simple quadratics, while the quadratic formula is a reliable method for any quadratic equation, even those that are difficult to factorise by inspection. Completing the square is a powerful technique with broader applications in algebra and calculus, but might be less efficient for straightforward factorisation. The best method depends on your comfort level with each technique and the complexity of the quadratic expression.
Expanding the Factorised Expression (Verification)
To verify that our factorisation is correct, we can expand the factored form (2x + 3)(3x - 2):
(2x + 3)(3x - 2) = 2x(3x) + 2x(-2) + 3(3x) + 3(-2) = 6x² - 4x + 9x - 6 = 6x² + 5x - 6
This matches the original expression, confirming that our factorisation is accurate.
Applications of Factorising Quadratic Expressions
Factorising quadratic expressions is a crucial skill with numerous applications in various areas of mathematics and beyond. Some key applications include:
-
Solving Quadratic Equations: Setting the quadratic expression equal to zero transforms it into a quadratic equation. Factorising allows us to find the roots (solutions) of the equation easily.
-
Simplifying Algebraic Expressions: Factorising can simplify complex algebraic expressions, making them easier to manipulate and solve.
-
Graphing Quadratic Functions: The factored form of a quadratic expression reveals the x-intercepts (where the graph crosses the x-axis) of the corresponding quadratic function.
-
Calculus: Factorisation is frequently used in calculus, particularly in differentiation and integration.
-
Real-world Problems: Quadratic equations are used to model many real-world phenomena, such as the trajectory of a projectile, the area of a shape, and many more. Factorisation plays a vital role in solving these problems.
Frequently Asked Questions (FAQ)
-
Q: What if the quadratic expression cannot be factorised easily? A: If trial-and-error fails, the quadratic formula will always provide the roots, even if the expression doesn't have rational factors.
-
Q: What does it mean if the discriminant (b² - 4ac) in the quadratic formula is negative? A: A negative discriminant indicates that the quadratic equation has no real roots. The roots are complex numbers involving the imaginary unit i.
-
Q: Is there a specific order I should follow when testing factor combinations in the trial-and-error method? A: While there's no strict order, it's generally helpful to start with factors closer to the square root of 'a' and 'c' to minimize the number of attempts.
-
Q: Can I use any of these methods to factorise any quadratic expression? A: Yes, all three methods can be applied to any quadratic expression, although the trial-and-error method might become less efficient for expressions with larger coefficients.
Conclusion
Factorising quadratic expressions like 6x² + 5x - 6 is a crucial skill in algebra. This article has demonstrated three different methods – trial and error, the quadratic formula, and completing the square – for achieving this. Understanding these methods allows you to confidently tackle various quadratic expressions, equipping you with a fundamental tool for solving equations, simplifying expressions, and tackling real-world problems that involve quadratic relationships. Remember to choose the method best suited to the specific problem and your own comfort level. Practice regularly, and you’ll master this essential algebraic skill. Further exploration into more complex polynomials will build upon this foundation.
Latest Posts
Latest Posts
-
What Is Spatial Niche Partitioning
Sep 16, 2025
-
Merry Go Round For Kids
Sep 16, 2025
-
Simplify 1 27 2 3
Sep 16, 2025
-
Best Xmas Gifts For Men
Sep 16, 2025
-
2x 3 X 3 2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factorise 6x 2 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.