Simplify 1 27 2 3
thesills
Sep 16, 2025 · 5 min read
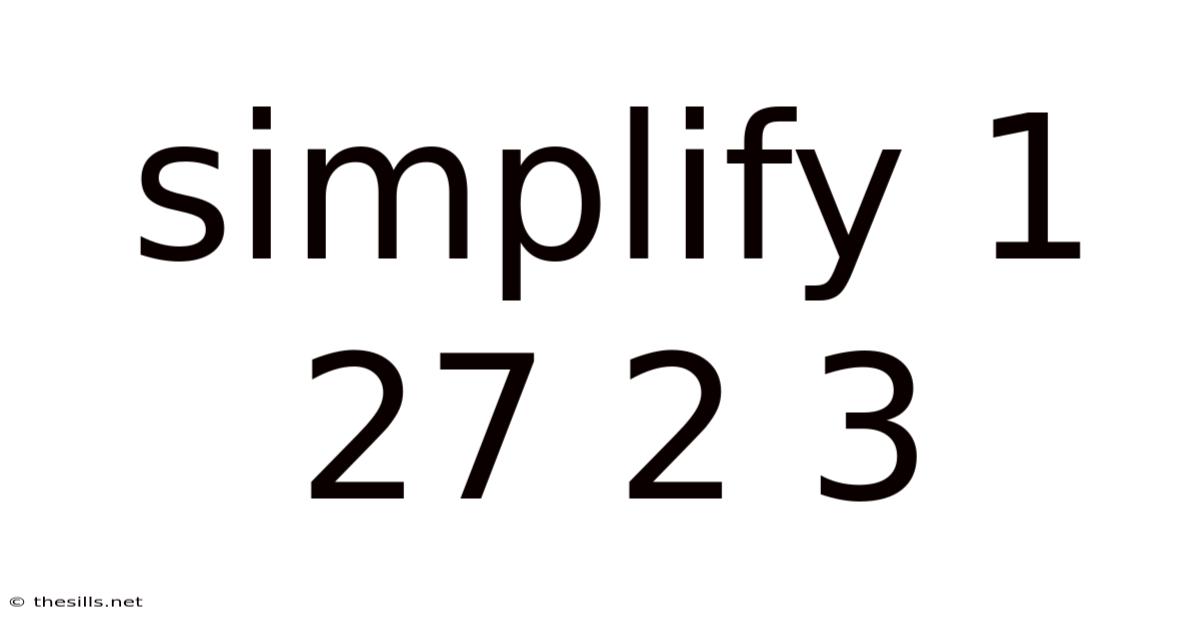
Table of Contents
Simplifying 1/27, 2/3: A Deep Dive into Fraction Simplification and Equivalent Fractions
Understanding how to simplify fractions is a fundamental skill in mathematics. This article will delve into the process of simplifying fractions, focusing specifically on the examples 1/27 and 2/3, while exploring the broader concepts of equivalent fractions, greatest common divisors (GCD), and the practical applications of fraction simplification. We'll break down the steps, provide explanations, and address frequently asked questions to ensure a comprehensive understanding for learners of all levels.
Introduction: What Does it Mean to Simplify a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). Simplifying a fraction, also known as reducing a fraction to its simplest form, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and work with in calculations. In essence, we're finding the most concise representation of the same fractional value. Let's explore this with our examples, 1/27 and 2/3.
Simplifying 1/27
The fraction 1/27 is already in its simplest form. Why? Because the numerator (1) and the denominator (27) have no common factors other than 1. In other words, their greatest common divisor (GCD) is 1. To illustrate further, let's examine the factors of 1 and 27:
- Factors of 1: 1
- Factors of 27: 1, 3, 9, 27
As you can see, the only number that divides both 1 and 27 evenly is 1. Therefore, 1/27 cannot be simplified further. This means it's already in its simplest or lowest terms.
Simplifying 2/3
Unlike 1/27, the fraction 2/3 can be analyzed for simplification. Let's find the factors of the numerator and denominator:
- Factors of 2: 1, 2
- Factors of 3: 1, 3
The only common factor between 2 and 3 is 1. Therefore, like 1/27, 2/3 is also in its simplest form. It cannot be reduced to a smaller equivalent fraction.
Understanding Equivalent Fractions
The concept of equivalent fractions is crucial for understanding simplification. Equivalent fractions represent the same value, even though they appear different. For instance, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. All these fractions represent half of a whole. Simplifying a fraction is essentially finding the equivalent fraction with the smallest possible numerator and denominator.
To create equivalent fractions, we multiply or divide both the numerator and denominator by the same non-zero number. This maintains the ratio and thus the value of the fraction. For example:
- Multiplying: 1/2 * 2/2 = 2/4
- Dividing: 6/9 ÷ 3/3 = 2/3
This principle is fundamental to simplifying fractions. We divide both the numerator and denominator by their greatest common divisor (GCD) to obtain the simplest form.
Finding the Greatest Common Divisor (GCD)
The GCD, also known as the highest common factor (HCF), is the largest number that divides both the numerator and denominator without leaving a remainder. Finding the GCD is a key step in simplifying fractions. There are several methods to find the GCD:
-
Listing Factors: This method involves listing all the factors of the numerator and denominator and identifying the largest common factor. This is suitable for smaller numbers.
-
Prime Factorization: This method involves expressing both the numerator and denominator as a product of their prime factors. The GCD is then the product of the common prime factors raised to the lowest power. This method is more efficient for larger numbers. Let's illustrate this with an example:
Let's say we want to simplify 12/18.
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6.
Now, divide both the numerator and denominator by the GCD:
12 ÷ 6 = 2 18 ÷ 6 = 3
Therefore, the simplified fraction is 2/3.
- Euclidean Algorithm: This is a more advanced method for finding the GCD, especially useful for larger numbers. It involves a series of divisions until the remainder is 0. The last non-zero remainder is the GCD.
Practical Applications of Fraction Simplification
Simplifying fractions isn't just an abstract mathematical exercise; it has numerous practical applications in various fields:
-
Baking and Cooking: Recipes often use fractions, and simplifying them makes measuring ingredients easier and more precise.
-
Construction and Engineering: Accurate calculations are crucial in these fields, and simplified fractions make calculations more efficient and reduce errors.
-
Finance and Accounting: Working with fractional shares, percentages, and proportions necessitates a thorough understanding of fraction simplification for accurate calculations.
-
Data Analysis and Statistics: Simplifying fractions is essential when dealing with ratios, proportions, and probabilities.
Frequently Asked Questions (FAQ)
Q: What if I simplify a fraction and get a whole number?
A: This means the numerator was a multiple of the denominator. For example, simplifying 6/3 results in 2, a whole number.
Q: Can I simplify a fraction with a negative number?
A: Yes, treat the negative sign separately. Simplify the fraction's absolute value and then add the negative sign back if needed. For example, -12/18 simplifies to -2/3.
Q: Is there a shortcut for simplifying fractions with small numbers?
A: For small numbers, it's often easy to visually identify common factors. However, the methods described above (listing factors or prime factorization) provide a systematic approach for any size numbers.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It represents the fraction in its most concise and efficient form.
Conclusion: Mastering Fraction Simplification
Mastering fraction simplification is essential for anyone pursuing a strong foundation in mathematics. It's a fundamental skill that extends far beyond the classroom, with applications in various aspects of life. By understanding the concepts of equivalent fractions and the greatest common divisor, and practicing the methods outlined in this article, you'll be well-equipped to tackle any fraction simplification challenge with confidence and accuracy. Remember, practice is key to mastering this skill. Work through numerous examples, gradually increasing the complexity of the fractions to solidify your understanding. With consistent effort, simplifying fractions will become second nature, enabling you to navigate mathematical problems more effectively and efficiently.
Latest Posts
Latest Posts
-
Convert Mm Hg To Pa
Sep 16, 2025
-
Example Of Gas Evolution Reaction
Sep 16, 2025
-
Tropical Rainforest Non Living Things
Sep 16, 2025
-
Definition Of Unit In Physics
Sep 16, 2025
-
Alkaline Earth Metals Valence Electrons
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Simplify 1 27 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.