Factorise 3x 2 10x 8
thesills
Sep 15, 2025 · 6 min read
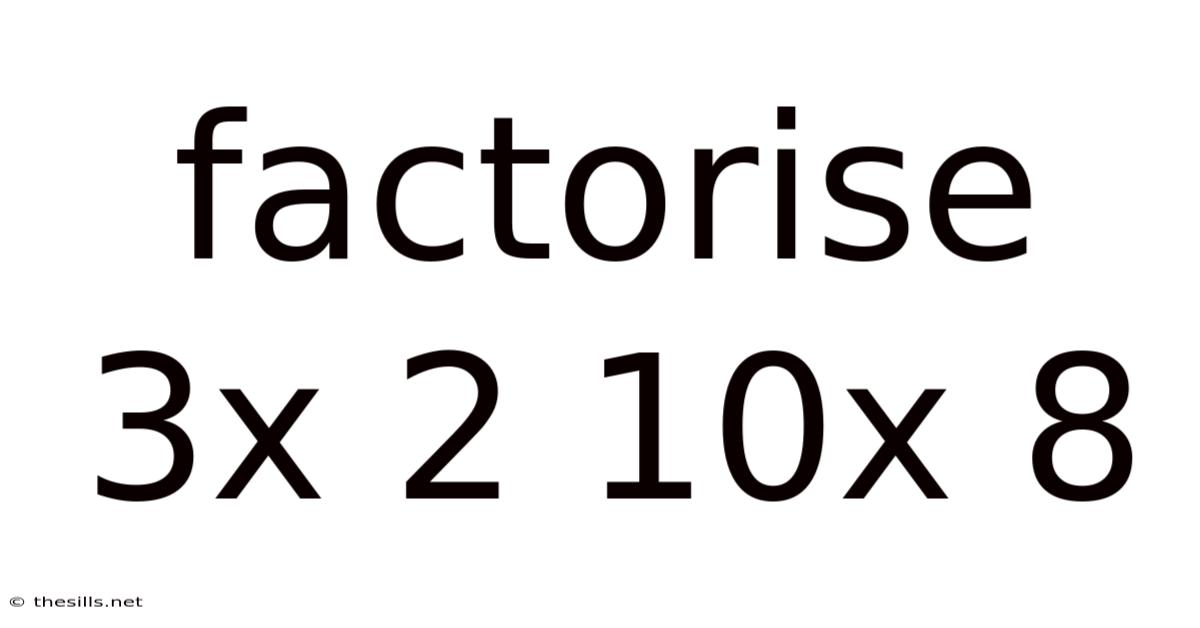
Table of Contents
Factorising 3x² + 10x + 8: A Comprehensive Guide
Factorising quadratic expressions is a fundamental skill in algebra. Understanding how to factorise allows you to solve quadratic equations, simplify expressions, and delve deeper into more advanced mathematical concepts. This comprehensive guide will walk you through the process of factorising the quadratic expression 3x² + 10x + 8, covering various methods and providing a thorough understanding of the underlying principles. We'll explore different approaches, highlighting their strengths and weaknesses, to equip you with the tools to tackle similar problems confidently. By the end, you'll not only know how to factorise this specific expression but also develop a robust understanding of quadratic factorisation in general.
Understanding Quadratic Expressions
Before we dive into factorising 3x² + 10x + 8, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, a = 3, b = 10, and c = 8. Factorising means expressing this quadratic expression as a product of two simpler expressions, typically two linear expressions (expressions of degree one).
Method 1: Factoring by Inspection (Trial and Error)
This method involves finding two binomials (expressions with two terms) whose product equals the original quadratic expression. We look for two numbers that add up to 'b' (the coefficient of x) and multiply to 'ac' (the product of the coefficient of x² and the constant term).
-
Step 1: Identify 'a', 'b', and 'c'. In 3x² + 10x + 8, a = 3, b = 10, and c = 8.
-
Step 2: Find two numbers that add up to 'b' and multiply to 'ac'. 'ac' = 3 * 8 = 24. We need two numbers that add up to 10 and multiply to 24. These numbers are 6 and 4 (6 + 4 = 10 and 6 * 4 = 24).
-
Step 3: Rewrite the middle term using these two numbers. We rewrite 10x as 6x + 4x: 3x² + 6x + 4x + 8
-
Step 4: Factor by grouping. Group the terms in pairs and factor out the common factors:
3x(x + 2) + 4(x + 2)
-
Step 5: Factor out the common binomial. Notice that (x + 2) is common to both terms. Factor it out:
(x + 2)(3x + 4)
Therefore, the factorised form of 3x² + 10x + 8 is (x + 2)(3x + 4).
Method 2: Using the Quadratic Formula
The quadratic formula is a powerful tool for solving quadratic equations and can also be used to find the factors. The quadratic formula states that for a quadratic equation ax² + bx + c = 0, the solutions for x are given by:
x = [-b ± √(b² - 4ac)] / 2a
While this doesn't directly give the factorised form, it provides the roots (the values of x that make the expression equal to zero). Once you have the roots, you can construct the factors.
-
Step 1: Identify 'a', 'b', and 'c'. As before, a = 3, b = 10, and c = 8.
-
Step 2: Apply the quadratic formula.
x = [-10 ± √(10² - 4 * 3 * 8)] / (2 * 3) x = [-10 ± √(100 - 96)] / 6 x = [-10 ± √4] / 6 x = (-10 ± 2) / 6
-
Step 3: Find the roots.
x₁ = (-10 + 2) / 6 = -8 / 6 = -4/3 x₂ = (-10 - 2) / 6 = -12 / 6 = -2
-
Step 4: Construct the factors. If x₁ and x₂ are the roots, then the factors are (x - x₁) and (x - x₂). Therefore:
(x - (-4/3)) = (x + 4/3) (x - (-2)) = (x + 2)
To get rid of the fraction, we can multiply the first factor by 3:
3(x + 4/3) = (3x + 4)
So the factorised form is (x + 2)(3x + 4). Note that this method is more complex than factoring by inspection, but it's a valuable tool when factoring by inspection proves difficult.
Method 3: Completing the Square
Completing the square is another powerful technique for solving quadratic equations and can be adapted to find factors. This method involves manipulating the quadratic expression to create a perfect square trinomial. However, for this particular expression, factoring by inspection or using the quadratic formula are more efficient. Completing the square is generally more useful when dealing with expressions where factoring by inspection is challenging.
A Deeper Look at the Solution: (x + 2)(3x + 4)
Let's verify our solution by expanding the factorised form:
(x + 2)(3x + 4) = x(3x + 4) + 2(3x + 4) = 3x² + 4x + 6x + 8 = 3x² + 10x + 8
This confirms that our factorisation is correct. The factors (x + 2) and (3x + 4) represent the linear expressions whose product equals the original quadratic expression.
Why Factorisation is Important
Factorisation is a crucial skill in algebra for several reasons:
-
Solving Quadratic Equations: Setting a factorised quadratic expression equal to zero allows you to easily solve for the roots (the values of x that satisfy the equation). For example, setting (x + 2)(3x + 4) = 0 gives us x = -2 and x = -4/3.
-
Simplifying Expressions: Factorisation can simplify complex algebraic expressions, making them easier to manipulate and understand.
-
Finding the x-intercepts of a Parabola: In coordinate geometry, the roots of a quadratic equation represent the x-intercepts (where the parabola crosses the x-axis) of the corresponding parabolic graph.
-
Foundation for Advanced Topics: Factorisation forms the basis for more advanced mathematical concepts such as partial fraction decomposition, calculus, and linear algebra.
Frequently Asked Questions (FAQ)
-
Q: Can I use any method to factorise a quadratic expression? A: While various methods exist, some are more efficient than others depending on the specific expression. Factoring by inspection is often the quickest method if the factors are relatively straightforward. The quadratic formula is a reliable method that always works, but it can be more time-consuming. Completing the square is generally less efficient for this type of problem.
-
Q: What if I can't find the factors by inspection? A: If you struggle to find the factors by inspection, the quadratic formula is a reliable alternative.
-
Q: What if the quadratic expression cannot be factorised using integers? A: Some quadratic expressions cannot be factorised using integers; in such cases, the quadratic formula will still provide the roots, and the factors will involve irrational numbers or fractions.
-
Q: Is there a way to check if my factorisation is correct? A: Yes, you can always expand your factorised form to verify that it matches the original expression.
Conclusion
Factorising quadratic expressions is a vital skill in algebra. This guide has explored different approaches to factorise 3x² + 10x + 8, including factoring by inspection, using the quadratic formula, and briefly discussing completing the square. We've emphasized that understanding the underlying principles and selecting the most efficient method is crucial. Mastering this skill will greatly enhance your ability to solve quadratic equations, simplify expressions, and progress to more advanced algebraic concepts. Remember, practice is key. The more you practice, the faster and more confident you'll become in factorising quadratic expressions. Don't be afraid to try different methods and check your work along the way. With consistent effort, you will develop a solid understanding of this fundamental algebraic technique.
Latest Posts
Latest Posts
-
Food Web In The Grasslands
Sep 15, 2025
-
What Is 15 Of 900
Sep 15, 2025
-
24 Is A Multiple Of
Sep 15, 2025
-
Where Are Transition Metals Located
Sep 15, 2025
-
Is Co2 Heavier Than O2
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Factorise 3x 2 10x 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.