What Is 15 Of 900
thesills
Sep 15, 2025 · 5 min read
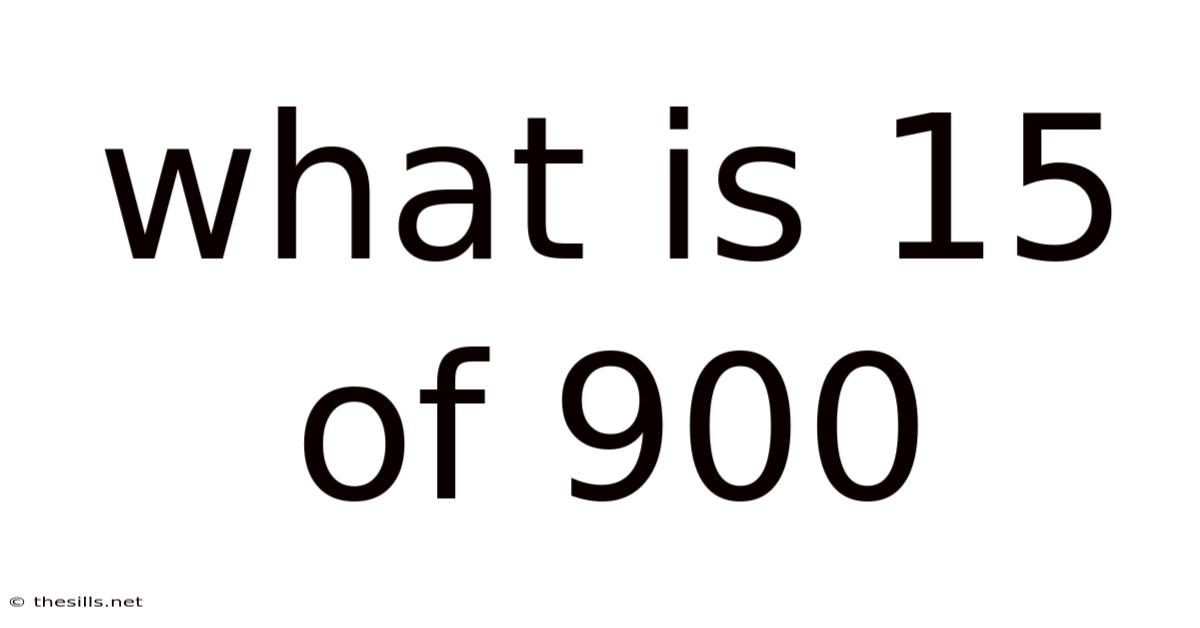
Table of Contents
What is 15% of 900? A Comprehensive Guide to Percentages and Their Applications
Finding 15% of 900 might seem like a simple arithmetic problem, but understanding the underlying principles of percentages opens up a world of applications in various fields, from finance and budgeting to scientific research and data analysis. This article will not only show you how to calculate 15% of 900 but also delve into the broader concept of percentages, providing you with the tools and knowledge to tackle similar problems confidently.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15. Understanding this fundamental equivalence is crucial for calculating percentages.
Methods for Calculating 15% of 900
There are several ways to calculate 15% of 900. Let's explore the most common methods:
Method 1: Converting Percentage to Decimal
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
- Step 1: Convert the percentage to a decimal: 15% = 15/100 = 0.15
- Step 2: Multiply the decimal by the number: 0.15 * 900 = 135
Therefore, 15% of 900 is 135.
Method 2: Using Fraction Equivalents
We can also use the fractional representation of the percentage.
- Step 1: Express the percentage as a fraction: 15% = 15/100
- Step 2: Simplify the fraction (if possible): 15/100 simplifies to 3/20
- Step 3: Multiply the fraction by the number: (3/20) * 900 = 3 * (900/20) = 3 * 45 = 135
Again, we find that 15% of 900 is 135.
Method 3: Proportion Method
This method utilizes the concept of proportions. We set up a proportion where x represents the unknown value (15% of 900).
- Step 1: Set up the proportion: 15/100 = x/900
- Step 2: Cross-multiply: 15 * 900 = 100 * x
- Step 3: Solve for x: 13500 = 100x => x = 13500/100 = 135
This confirms that 15% of 900 is 135.
Choosing the Best Method
All three methods yield the same result. The best method depends on personal preference and the context of the problem. The decimal method is generally the quickest and easiest for most people, while the fraction method can be beneficial for simplifying calculations when dealing with easily reducible fractions. The proportion method is excellent for understanding the underlying mathematical relationships.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-life situations:
-
Finance: Calculating interest earned on savings accounts, determining discounts on purchases, understanding taxes, analyzing investment returns, and calculating loan repayments all rely heavily on percentage calculations. For example, if a store offers a 15% discount on an item priced at $900, the discount amount is $135, resulting in a final price of $765.
-
Business: Businesses use percentages to track sales growth, analyze market share, calculate profit margins, and determine pricing strategies. Understanding percentage change is essential for assessing business performance and making informed decisions.
-
Science: Percentages are frequently used in scientific research to represent data, such as the percentage of a population exhibiting a certain characteristic or the percentage change in a measured quantity over time. Error rates and confidence intervals are often expressed as percentages.
-
Everyday Life: Calculating tips in restaurants, understanding nutrition labels (e.g., the percentage of daily recommended intake of nutrients), figuring out sales tax, and comparing prices based on unit cost all involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 900 is a relatively simple problem, the principles extend to more complex scenarios:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example, what percentage is 135 of 900? This involves dividing 135 by 900 and multiplying by 100 (135/900 * 100 = 15%).
-
Finding the Original Number: You might know the percentage and the resulting value and need to find the original number. For example, if 15% of a number is 135, what is the original number? This is solved by dividing 135 by 0.15 (135/0.15 = 900).
-
Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values and expressing it as a percentage of the original value. For example, if a value increases from 800 to 900, the percentage increase is ((900-800)/800) * 100 = 12.5%.
-
Compound Percentages: Compound percentages involve applying a percentage to a value repeatedly, taking into account the accumulated changes. This is commonly seen in compound interest calculations.
Frequently Asked Questions (FAQs)
-
Q: What is the easiest way to calculate percentages?
- A: The easiest method is typically converting the percentage to a decimal and multiplying it by the number.
-
Q: Can I use a calculator to calculate percentages?
- A: Yes, most calculators have a percentage function (%) that simplifies the process.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key. Work through various percentage problems of increasing complexity, using different methods to solidify your understanding. Focus on understanding the underlying concepts of fractions and decimals.
Conclusion
Calculating 15% of 900, resulting in 135, is a fundamental application of percentage calculations. However, understanding the broader principles of percentages is crucial for navigating a wide range of situations in various fields. Mastering percentage calculations not only improves your mathematical skills but also enhances your ability to analyze data, make informed decisions, and effectively apply mathematical concepts to real-world problems. From managing your personal finances to excelling in your professional life, a solid grasp of percentages is an invaluable asset. Remember to practice regularly and explore different methods to find the approach that best suits your learning style.
Latest Posts
Latest Posts
-
Objective Of Non Profit Organization
Sep 15, 2025
-
196 Is The Square Of
Sep 15, 2025
-
An Animal Beginning With Y
Sep 15, 2025
-
Mass Of One Water Molecule
Sep 15, 2025
-
What Is Degree Of Ionization
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 900 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.