Factoring 2x 2 5x 2
thesills
Sep 12, 2025 · 7 min read
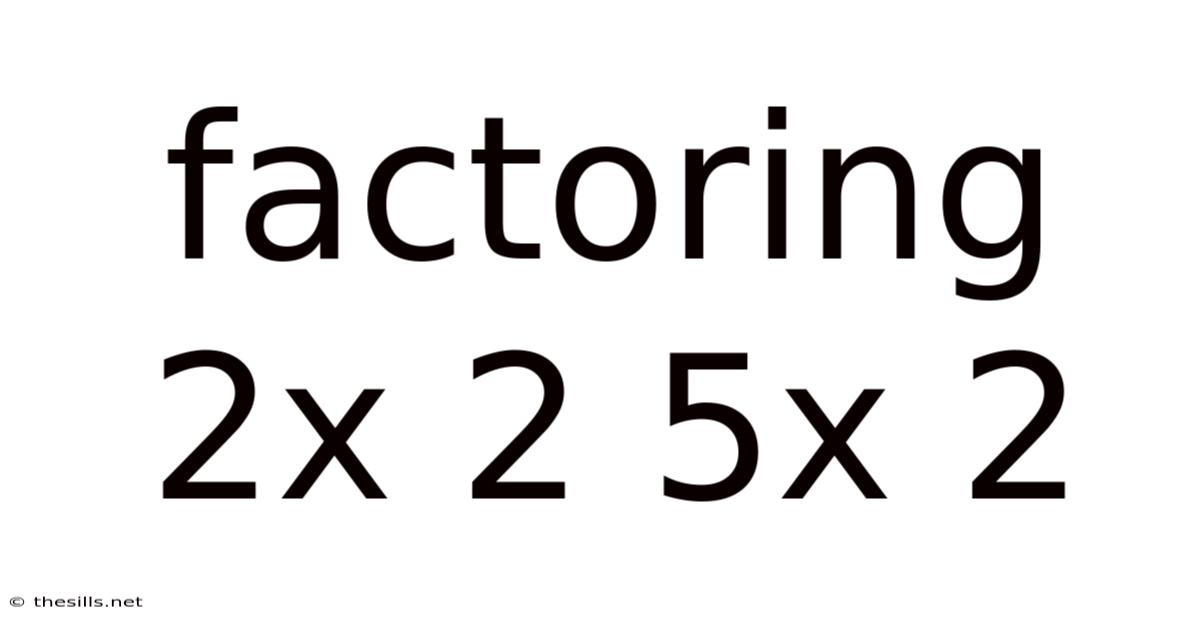
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 5x + 2
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding many higher-level mathematical concepts. This comprehensive guide will walk you through the process of factoring the specific quadratic expression 2x² + 5x + 2, explaining the underlying principles and providing you with the tools to factor similar expressions. We'll explore different methods, address common difficulties, and delve into the underlying mathematical reasoning. By the end, you'll not only understand how to factor this particular expression but also gain the confidence to tackle a wide range of quadratic factoring problems.
Introduction to Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It takes the general form ax² + bx + c, where a, b, and c are constants, and a is not equal to zero. Factoring a quadratic expression involves rewriting it as a product of two simpler expressions, usually two binomials. This process is the reverse of expanding binomials using the FOIL (First, Outer, Inner, Last) method.
Factoring 2x² + 5x + 2: The Methods
Let's now tackle the specific expression: 2x² + 5x + 2. We'll explore two primary methods for factoring this type of quadratic:
1. The AC Method (also known as the Grouping Method):
This method is particularly useful when the coefficient of the x² term (a) is not equal to 1. Here's how it works:
-
Step 1: Find the product AC. In our expression, a = 2 and c = 2, so AC = 2 * 2 = 4.
-
Step 2: Find two numbers that add up to B and multiply to AC. Our b is 5. We need two numbers that add up to 5 and multiply to 4. These numbers are 4 and 1 (4 + 1 = 5 and 4 * 1 = 4).
-
Step 3: Rewrite the middle term using these two numbers. We rewrite 5x as 4x + 1x:
2x² + 4x + 1x + 2
-
Step 4: Factor by grouping. Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
2x(x + 2) + 1(x + 2)
-
Step 5: Factor out the common binomial. Notice that both terms now share the binomial (x + 2). Factor this out:
(x + 2)(2x + 1)
Therefore, the factored form of 2x² + 5x + 2 is (x + 2)(2x + 1).
2. Trial and Error Method:
This method involves systematically trying different combinations of binomial factors until you find the correct one. It's often faster once you gain experience, but it can be less systematic than the AC method.
-
Step 1: Set up the binomial factors. Since the coefficient of x² is 2, we know one binomial will start with 2x and the other with x:
(2x )(x )
-
Step 2: Consider the factors of the constant term. The constant term is 2. Its factors are 1 and 2.
-
Step 3: Test different combinations. We need to place the factors of 2 (1 and 2) into the parentheses so that when we use the FOIL method, we get the original expression. Let's try different combinations:
- (2x + 1)(x + 2): Using FOIL, this gives 2x² + 4x + x + 2 = 2x² + 5x + 2. This is correct!
- (2x + 2)(x + 1): Using FOIL, this gives 2x² + 2x + 2x + 2 = 2x² + 4x + 2. This is incorrect.
Therefore, the factored form is again (x + 2)(2x + 1). Note that the order of the factors doesn't matter; (2x + 1)(x + 2) is equivalent to (x + 2)(2x + 1).
Understanding the Mathematics Behind Factoring
The success of both methods hinges on the distributive property of multiplication. The FOIL method (First, Outer, Inner, Last) is a specific application of this property. When we expand (x + 2)(2x + 1), we're essentially distributing each term in the first binomial across the second:
x(2x + 1) + 2(2x + 1) = 2x² + x + 4x + 2 = 2x² + 5x + 2
Factoring reverses this process. We're looking for two binomials whose product is the original quadratic expression. The AC method systematically finds these binomials by manipulating the middle term and using the grouping technique to reveal the common binomial factor. The trial-and-error method relies on intuition and a bit of educated guessing, guided by the factors of the leading coefficient and the constant term.
Solving Quadratic Equations using Factoring
Once we have factored a quadratic expression, we can use it to solve quadratic equations. For example, if we have the equation 2x² + 5x + 2 = 0, we can use the factored form (x + 2)(2x + 1) = 0. The zero-product property states that if the product of two factors is zero, then at least one of the factors must be zero. This allows us to solve for x:
- x + 2 = 0 => x = -2
- 2x + 1 = 0 => 2x = -1 => x = -1/2
Therefore, the solutions to the equation 2x² + 5x + 2 = 0 are x = -2 and x = -1/2.
Dealing with Special Cases
While the AC method and trial-and-error work for most quadratics, some special cases merit attention:
-
Perfect Square Trinomials: These are quadratics that can be factored into the square of a binomial, like (ax + b)². Recognizing these can simplify the factoring process significantly. For example, x² + 6x + 9 = (x + 3)².
-
Difference of Squares: Expressions of the form a² - b² can be factored as (a + b)(a - b). This is a particularly easy factoring pattern to recognize.
-
Prime Quadratics: Some quadratics cannot be factored using integers. These are called prime quadratics. In such cases, other methods, like the quadratic formula, are necessary to find the roots or solutions.
Frequently Asked Questions (FAQ)
Q: What if the coefficient of x² is 1?
A: If the coefficient of x² is 1, the factoring process simplifies. You can directly look for two numbers that add up to the coefficient of x and multiply to the constant term. For example, in x² + 5x + 6, we look for two numbers that add to 5 and multiply to 6 (these are 2 and 3), leading to the factored form (x + 2)(x + 3).
Q: Is there a way to check my answer?
A: Yes! Always expand your factored form using the FOIL method. If it gives you the original quadratic expression, your factoring is correct.
Q: What if I'm struggling with factoring?
A: Practice is key! Start with simpler quadratics and gradually increase the difficulty. Use online resources, textbooks, and seek help from teachers or tutors if needed. Understanding the underlying mathematical principles is crucial for success.
Q: Are there other methods for factoring quadratics?
A: Yes, the quadratic formula is a powerful tool that can be used to find the roots of any quadratic equation, even those that are difficult or impossible to factor. Completing the square is another method that can be useful in certain situations.
Q: Why is factoring important?
A: Factoring is a fundamental algebraic skill with broad applications in various fields. It's essential for solving quadratic equations, simplifying expressions, graphing parabolas, and understanding more advanced mathematical concepts like calculus.
Conclusion
Factoring quadratic expressions, even seemingly complex ones like 2x² + 5x + 2, becomes manageable with the right approach and understanding. Both the AC method and trial-and-error offer effective pathways to finding the factored form. Remember to always check your work by expanding the factored form and comparing it to the original expression. Mastering quadratic factoring is a significant step towards building a strong foundation in algebra and unlocking the doors to more advanced mathematical concepts. Consistent practice and a clear understanding of the underlying principles will empower you to confidently tackle any quadratic factoring challenge you encounter. Don't hesitate to review these steps, practice with various examples, and seek help when needed. Your algebraic prowess will undoubtedly improve with dedication and perseverance.
Latest Posts
Latest Posts
-
X Cos X Dx Integral
Sep 12, 2025
-
X 3 6x 2 5x
Sep 12, 2025
-
Most Abundant Form Of Tissue
Sep 12, 2025
-
Simple Cubic Cell Coordination Number
Sep 12, 2025
-
Baking Soda Or Washing Soda
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Factoring 2x 2 5x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.