X 3 6x 2 5x
thesills
Sep 12, 2025 · 5 min read
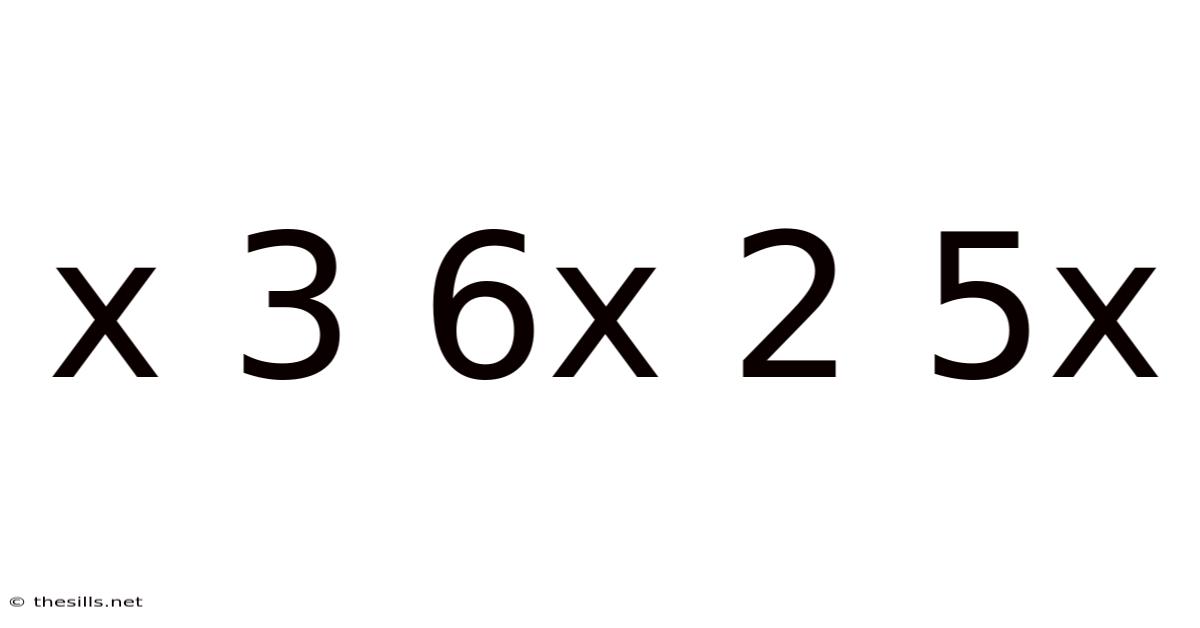
Table of Contents
Decoding the Expression: x³ + 6x² + 5x
This article explores the algebraic expression x³ + 6x² + 5x, delving into its factorization, its graphical representation, and its applications in various mathematical contexts. Understanding this seemingly simple expression unlocks deeper insights into polynomial manipulation, calculus, and even real-world problem-solving. We'll break down the process step-by-step, making it accessible to students of all levels.
Introduction: Unveiling the Polynomial
The expression x³ + 6x² + 5x is a polynomial of degree three, also known as a cubic polynomial. This means the highest power of the variable x is 3. Polynomials are fundamental building blocks in algebra, forming the basis for many mathematical concepts. Understanding how to manipulate and analyze polynomials is crucial for success in higher-level mathematics and its applications in fields like engineering, physics, and economics. This article will guide you through the key aspects of understanding and working with x³ + 6x² + 5x.
Factorization: Finding the Roots
The most significant step in understanding this cubic polynomial is to factorize it. Factorization involves expressing the polynomial as a product of simpler expressions. This allows us to find the roots or zeros of the polynomial – the values of x that make the expression equal to zero.
The first and easiest step in factorization is to look for a common factor. In this case, we observe that x is a common factor to all terms:
x³ + 6x² + 5x = x(x² + 6x + 5)
Now, we need to factor the quadratic expression (x² + 6x + 5). We are looking for two numbers that add up to 6 (the coefficient of x) and multiply to 5 (the constant term). These numbers are 5 and 1. Therefore, the quadratic can be factored as:
x² + 6x + 5 = (x + 5)(x + 1)
Putting it all together, the complete factorization of x³ + 6x² + 5x is:
x³ + 6x² + 5x = x(x + 5)(x + 1)
Finding the Roots (Zeros)
The roots of the polynomial are the values of x that make the expression equal to zero. Since the expression is now completely factored, we can easily find the roots by setting each factor equal to zero:
- x = 0
- x + 5 = 0 => x = -5
- x + 1 = 0 => x = -1
Therefore, the roots of the polynomial x³ + 6x² + 5x are 0, -1, and -5. These roots represent the x-intercepts of the graph of the polynomial.
Graphical Representation: Visualizing the Polynomial
The graph of a cubic polynomial is a curve. Understanding the shape of the graph helps visualize the behavior of the polynomial. Knowing the roots helps us sketch the graph. Since the coefficient of x³ (the leading coefficient) is positive, the graph will rise to the right and fall to the left. The roots (0, -1, and -5) are the points where the graph intersects the x-axis.
The graph will pass through the points (0,0), (-1,0), and (-5,0). Between these points, the graph will change direction, creating two turning points. While a precise sketch requires calculus (finding the derivative to locate the turning points), we can create a reasonable approximation based on the knowledge of the roots. The curve will start from the bottom left, pass through (-5,0), curve upwards, pass through (-1,0), curve downwards, and finally pass through (0,0) as it rises to the right.
Applications: Real-World Context
Cubic polynomials, and their factorization, have many applications in various fields:
- Engineering: Cubic equations are used in the design of structures, especially for calculating the strength and stability of beams and columns.
- Physics: They model certain physical phenomena, such as the trajectory of projectiles.
- Economics: Cubic functions can represent production functions, relating inputs (like labor and capital) to output.
- Computer Graphics: Cubic curves are used in computer-aided design (CAD) and other graphical applications.
Calculus and the Polynomial: Derivatives and Integrals
Understanding calculus allows us to delve deeper into the properties of this polynomial.
-
Derivative: The derivative of x³ + 6x² + 5x is 3x² + 12x + 5. The derivative gives the slope of the tangent line to the curve at any point. Setting the derivative to zero helps us find the stationary points (where the slope is zero), which are the local maxima and minima of the curve.
-
Integral: The indefinite integral of x³ + 6x² + 5x is (1/4)x⁴ + 2x³ + (5/2)x² + C, where C is the constant of integration. The definite integral represents the area under the curve between two points. This concept is essential in calculating quantities like work, volume, and other physical measures.
Further Exploration: More Complex Cubic Polynomials
While this article focused on x³ + 6x² + 5x, the principles discussed are applicable to other cubic polynomials. However, factorization of more complex cubic polynomials might require more advanced techniques like the Rational Root Theorem or numerical methods.
Frequently Asked Questions (FAQ)
Q: What if the polynomial couldn't be easily factored?
A: For more complex cubic polynomials, numerical methods or the cubic formula (a complex formula for finding roots) might be necessary.
Q: Are there always three real roots for a cubic polynomial?
A: No. A cubic polynomial can have three real roots, one real root and two complex roots (complex conjugates), or three real roots (some of which may be repeated).
Q: How can I use the graph to solve inequalities involving the polynomial?
A: By examining the graph, you can determine the intervals where the polynomial is positive (above the x-axis) or negative (below the x-axis). This is helpful for solving inequalities like x³ + 6x² + 5x > 0.
Conclusion: Mastering the Cubic
Understanding the polynomial x³ + 6x² + 5x extends far beyond simple algebraic manipulation. Through factorization, we uncover its roots, providing crucial information for graphical representation and understanding its behavior. Its application across various fields highlights its significance in mathematics and beyond. Exploring its derivative and integral opens doors to calculus and a deeper understanding of its properties. This detailed exploration equips you with a solid foundation for tackling more complex polynomial expressions and their applications in diverse areas of study. Remember, the key lies in understanding the fundamental concepts and applying them methodically.
Latest Posts
Latest Posts
-
1 U Is Equal To
Sep 12, 2025
-
68 Degrees Fahrenheit To Kelvin
Sep 12, 2025
-
Co Bond Polar Or Nonpolar
Sep 12, 2025
-
How Do Fireflies Emit Light
Sep 12, 2025
-
Which Planet Called Blue Planet
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 3 6x 2 5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.