Factor X 2 X 56
thesills
Sep 12, 2025 · 6 min read
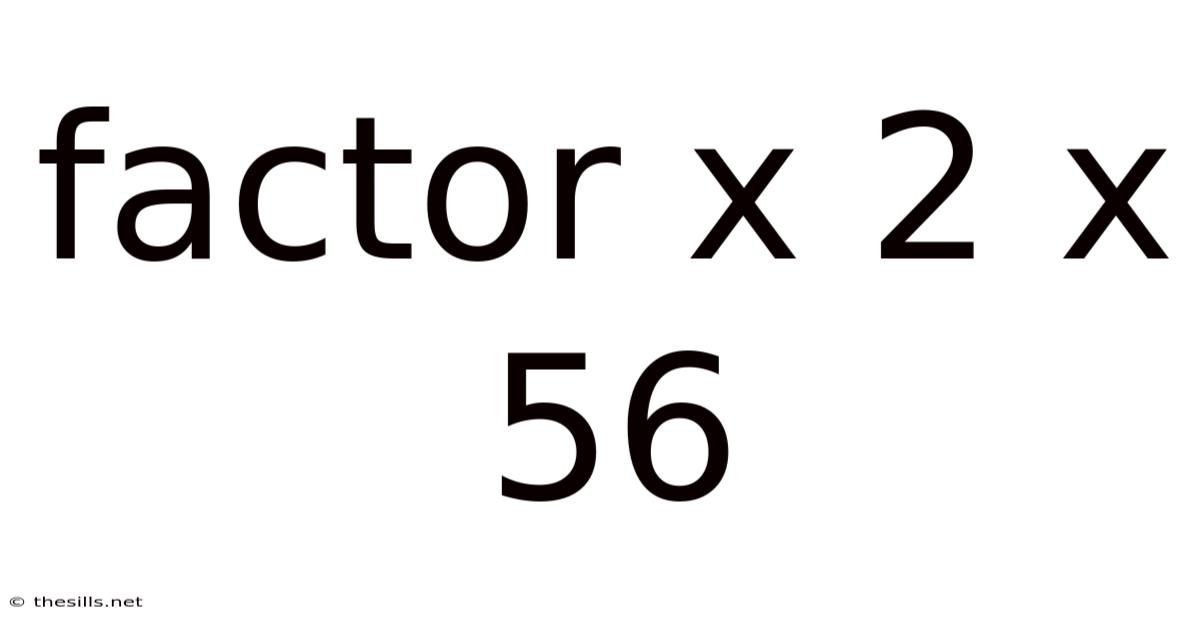
Table of Contents
Decoding Factor X: A Deep Dive into 2 x 56 and Beyond
Understanding multiplication is fundamental to mathematics, forming the bedrock for more complex calculations and concepts. This article delves into the seemingly simple equation, 2 x 56, exploring not just the answer but the underlying principles, different approaches to solving it, and the broader implications within the realm of arithmetic and beyond. We'll cover various methods, from basic multiplication to the distributive property, and discuss how this seemingly straightforward problem can illuminate more advanced mathematical ideas. This comprehensive guide is perfect for anyone looking to strengthen their foundational math skills or delve deeper into the beauty of numerical relationships.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is simply repeated addition. The equation 2 x 56 means adding 56 to itself two times. This can be visually represented:
56 + 56 = 112
This approach, while straightforward, becomes less efficient as the numbers grow larger. For instance, calculating 23 x 457 using repeated addition would be incredibly time-consuming. Therefore, understanding more efficient methods is crucial.
Method 1: Traditional Multiplication Algorithm
The standard multiplication algorithm is a systematic approach that breaks down larger multiplication problems into smaller, manageable steps. For 2 x 56, this method proceeds as follows:
-
Multiply the ones digit: 2 x 6 = 12. Write down the '2' and carry-over the '1'.
-
Multiply the tens digit: 2 x 5 = 10. Add the carry-over '1': 10 + 1 = 11.
-
Combine the results: The final answer is 112.
Method 2: Distributive Property
The distributive property is a powerful tool in mathematics that allows us to break down complex calculations into simpler ones. It states that a(b + c) = ab + ac. We can apply this to 2 x 56 by breaking 56 into 50 + 6:
2 x 56 = 2 x (50 + 6) = (2 x 50) + (2 x 6) = 100 + 12 = 112
This method demonstrates the flexibility and elegance of algebraic principles even in elementary arithmetic. It’s particularly useful when dealing with larger numbers or more complex expressions.
Method 3: Using Multiplication Tables
Memorizing multiplication tables is a cornerstone of basic arithmetic. If you know your multiplication facts, you can instantly recognize that 2 x 56 = 112. While this method relies on prior memorization, it’s the quickest and most efficient approach for simple problems like this. The speed and accuracy gained from knowing multiplication tables significantly improve your ability to tackle more complex calculations later.
Method 4: Lattice Multiplication
Lattice multiplication is a visually appealing and effective method, particularly beneficial for multiplying larger numbers. Although seemingly more complex, it’s a systematic approach that minimizes the risk of errors. While less efficient for 2 x 56, understanding it provides insight into alternative multiplication techniques.
-
Draw a grid with rows and columns corresponding to the digits of the numbers being multiplied (2 and 56 in this case).
-
Multiply each digit individually and write the result within the corresponding cell, splitting tens and ones digits diagonally.
-
Add the diagonal entries to obtain the final product.
This method reduces the mental burden of carrying over digits, making it a valuable technique for learners who struggle with traditional multiplication.
Beyond the Calculation: Exploring the Concept of Factors
The equation 2 x 56 highlights the concept of factors. In this case, 2 and 56 are factors of 112. A factor is a number that divides another number without leaving a remainder. Understanding factors is crucial in various areas of mathematics, including prime factorization, greatest common divisor (GCD), and least common multiple (LCM) calculations. 112 has multiple factor pairs, including (1, 112), (2, 56), (4, 28), (7, 16), and (8, 14).
The prime factorization of 112 is 2⁴ x 7, illustrating the fundamental building blocks of this number. This decomposition into prime factors is unique to each number and has far-reaching implications in number theory and cryptography.
Real-World Applications: Where Does 2 x 56 Matter?
While seemingly simple, understanding multiplication, and specifically problems like 2 x 56, has numerous real-world applications:
-
Everyday Calculations: Calculating the total cost of two identical items, determining the total distance traveled in two equal trips, or splitting a bill evenly.
-
Measurement and Conversion: Converting units of measurement, such as calculating the total length of two pieces of wood each 56 cm long.
-
Geometric Calculations: Calculating the area of a rectangle with a width of 2 units and a length of 56 units.
-
Finance and Budgeting: Calculating interest, total earnings, or expenses.
-
Engineering and Construction: Various calculations involving dimensions, materials, and quantities.
Extending the Concept: Working with Larger Numbers and Variables
The principles demonstrated with 2 x 56 extend to much larger numbers and even algebraic expressions. Consider calculating 2 x 5600 or 2x (x + 28). The same methods, such as the distributive property, apply, showcasing the versatility and scalability of the underlying mathematical concepts.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to solve 2 x 56?
A: If you know your multiplication tables, the quickest way is to recall the answer directly: 112.
Q: Can I use a calculator for this problem?
A: Absolutely! Calculators are valuable tools for efficient computation, especially with larger numbers.
Q: What are some alternative methods for multiplying larger numbers?
A: For larger numbers, the lattice method, the distributive property, or breaking down the numbers into smaller, more manageable parts are efficient strategies. Long multiplication remains a standard and effective method.
Q: Why is it important to learn multiplication?
A: Multiplication is a fundamental building block of mathematics. Mastering it is crucial for success in various academic disciplines and real-world applications.
Q: How can I improve my multiplication skills?
A: Practice regularly, memorize multiplication tables, and explore different multiplication methods to find what works best for you. Use flashcards, online games, or workbooks to reinforce learning.
Conclusion: The Significance of Simplicity
The equation 2 x 56, while seemingly insignificant on its own, serves as a gateway to understanding fundamental mathematical concepts and techniques. Mastering multiplication and exploring different methods for solving such problems not only strengthens basic arithmetic skills but also paves the way for understanding more complex mathematical ideas. From the distributive property to factor analysis and prime factorization, the seemingly simple act of multiplying 2 by 56 unlocks a wealth of mathematical knowledge, showcasing the beauty and interconnectedness of numbers. By understanding these underlying principles, you build a strong foundation for future mathematical endeavors. Remember that consistent practice and a curious approach are key to mastering mathematical concepts and unlocking your full potential.
Latest Posts
Latest Posts
-
4 X 3 X 4
Sep 13, 2025
-
What Are Horizontal Rows Called
Sep 13, 2025
-
122 Degrees Fahrenheit To Celsius
Sep 13, 2025
-
Copper Oxide And Sulfuric Acid
Sep 13, 2025
-
Proximal Vs Distal Convoluted Tubule
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 X 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.