Factor X 2 13x 40
thesills
Sep 13, 2025 · 6 min read
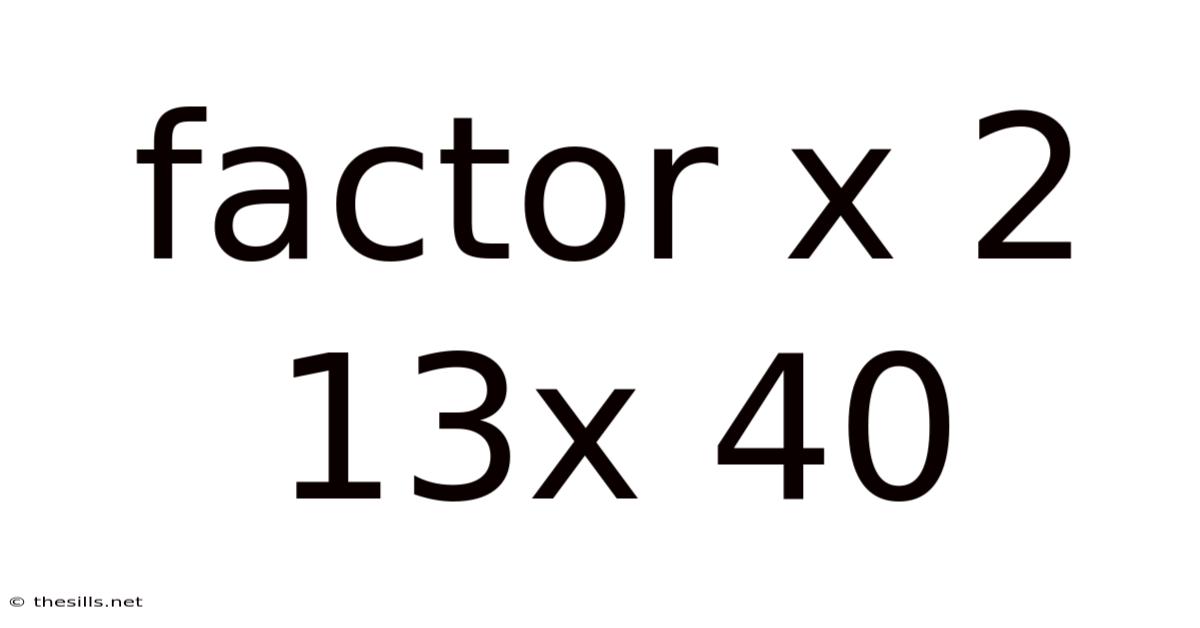
Table of Contents
Factoring the Quadratic Expression: x² + 13x + 40
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This seemingly simple process opens doors to solving quadratic equations, graphing parabolas, and tackling more complex mathematical problems. This comprehensive guide will walk you through factoring the specific quadratic expression, x² + 13x + 40, step-by-step, exploring the underlying principles and providing you with the tools to factor similar expressions with confidence. We'll cover various methods, explain the reasoning behind each step, and answer frequently asked questions. By the end, you'll not only know the factors of x² + 13x + 40 but also possess a solid understanding of quadratic factoring.
Understanding Quadratic Expressions
Before diving into the factoring process, let's establish a foundation. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants. In our case, x² + 13x + 40, a = 1, b = 13, and c = 40.
Factoring a quadratic expression means rewriting it as a product of two simpler expressions, typically two binomials. This process reverses the multiplication of binomials. For example, if we expand (x + 5)(x + 8), we get x² + 8x + 5x + 40, which simplifies to x² + 13x + 40. Our goal is to find these original binomial factors.
Method 1: The Factoring Method (Trial and Error)
This method relies on understanding the relationship between the coefficients and the constant term in the quadratic expression. We're looking for two numbers that add up to 'b' (13 in this case) and multiply to 'c' (40).
-
Step 1: Identify the factors of 'c'. The factors of 40 are: 1 and 40, 2 and 20, 4 and 10, 5 and 8.
-
Step 2: Find the pair that adds up to 'b'. Among these pairs, only 5 and 8 add up to 13.
-
Step 3: Construct the binomial factors. Since both 5 and 8 are positive, our binomial factors are (x + 5) and (x + 8).
-
Step 4: Verify the factors. Expand (x + 5)(x + 8) to confirm it equals x² + 13x + 40. (x + 5)(x + 8) = x² + 8x + 5x + 40 = x² + 13x + 40.
Therefore, the factored form of x² + 13x + 40 is (x + 5)(x + 8).
Method 2: The AC Method (for more complex quadratics)
The AC method is particularly useful when the coefficient 'a' is not equal to 1. While not strictly necessary for x² + 13x + 40 (since a = 1), it's a valuable technique to learn for more complex quadratic expressions.
-
Step 1: Multiply 'a' and 'c'. In our case, a * c = 1 * 40 = 40.
-
Step 2: Find two numbers that add up to 'b' and multiply to 'ac'. We need two numbers that add to 13 and multiply to 40. As before, these numbers are 5 and 8.
-
Step 3: Rewrite the middle term. Rewrite 13x as 5x + 8x: x² + 5x + 8x + 40.
-
Step 4: Factor by grouping. Group the terms in pairs and factor out the common factors:
- x(x + 5) + 8(x + 5)
-
Step 5: Factor out the common binomial. Notice that (x + 5) is common to both terms: (x + 5)(x + 8).
This again confirms that the factored form of x² + 13x + 40 is (x + 5)(x + 8).
Method 3: Using the Quadratic Formula (for finding roots)
While not directly factoring the expression, the quadratic formula can help you find the roots (solutions) of the quadratic equation x² + 13x + 40 = 0. These roots are directly related to the factors. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
-
Step 1: Substitute the values. a = 1, b = 13, c = 40.
-
Step 2: Calculate. x = [-13 ± √(13² - 4 * 1 * 40)] / 2 * 1 x = [-13 ± √(169 - 160)] / 2 x = [-13 ± √9] / 2 x = (-13 ± 3) / 2
-
Step 3: Find the roots. x₁ = (-13 + 3) / 2 = -5 x₂ = (-13 - 3) / 2 = -8
-
Step 4: Relate roots to factors. The roots are -5 and -8. Therefore, the factors are (x + 5) and (x + 8).
The Significance of Factoring
Factoring quadratic expressions is crucial for several reasons:
-
Solving Quadratic Equations: Setting a quadratic expression equal to zero creates a quadratic equation. Factoring allows us to easily find the solutions (roots) of the equation. For example, solving x² + 13x + 40 = 0 leads to (x + 5)(x + 8) = 0, which gives us x = -5 and x = -8.
-
Graphing Parabolas: The factored form of a quadratic expression reveals the x-intercepts (where the parabola crosses the x-axis) of its graph. The x-intercepts are the roots of the corresponding quadratic equation. In our case, the parabola y = x² + 13x + 40 crosses the x-axis at x = -5 and x = -8.
-
Simplifying Algebraic Expressions: Factoring can simplify more complex algebraic expressions, making them easier to manipulate and solve.
-
Foundation for Advanced Algebra: Understanding factoring is essential for mastering more advanced algebraic concepts, including polynomial division, partial fractions, and calculus.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression can't be factored easily? Not all quadratic expressions can be factored using simple integers. In such cases, you might need to use the quadratic formula to find the roots or employ more advanced factoring techniques.
-
Can I use a calculator or software to factor quadratics? While calculators and software can assist with factoring, understanding the underlying process is crucial for developing your mathematical skills. These tools should be used to check your work, not replace the learning process.
-
What if the coefficient of x² is negative? It's generally preferred to factor out a -1 first to make the leading coefficient positive, simplifying the factoring process.
-
What if 'c' is zero? If 'c' is zero, the quadratic expression can be factored simply by factoring out the common 'x' term. For example, x² + 5x = x(x + 5).
-
What if 'b' is zero? If 'b' is zero, the quadratic expression is a difference of squares (or a perfect square), which has a specific factoring pattern. For example, x² - 16 = (x - 4)(x + 4).
Conclusion
Factoring the quadratic expression x² + 13x + 40 demonstrates a fundamental algebraic skill with far-reaching applications. Through the various methods explored—the factoring method, the AC method, and even the indirect approach using the quadratic formula—we've demonstrated that the factored form is (x + 5)(x + 8). Understanding these methods and the principles behind them empowers you to tackle a wide range of quadratic expressions and solve related problems confidently. Remember to practice regularly to strengthen your skills and build a solid foundation in algebra. The more you practice, the quicker and more intuitive the process will become. Don't hesitate to revisit this guide and explore the different methods to solidify your understanding of quadratic factoring.
Latest Posts
Latest Posts
-
As Disposable Income Increases Consumption
Sep 13, 2025
-
The Year Of The Book
Sep 13, 2025
-
Integral Of 1 1 Tanx
Sep 13, 2025
-
Potassium Hydroxide And Sodium Hydroxide
Sep 13, 2025
-
How To Find Ionization Energies
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 13x 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.