Factor X 2 10x 25
thesills
Sep 17, 2025 · 6 min read
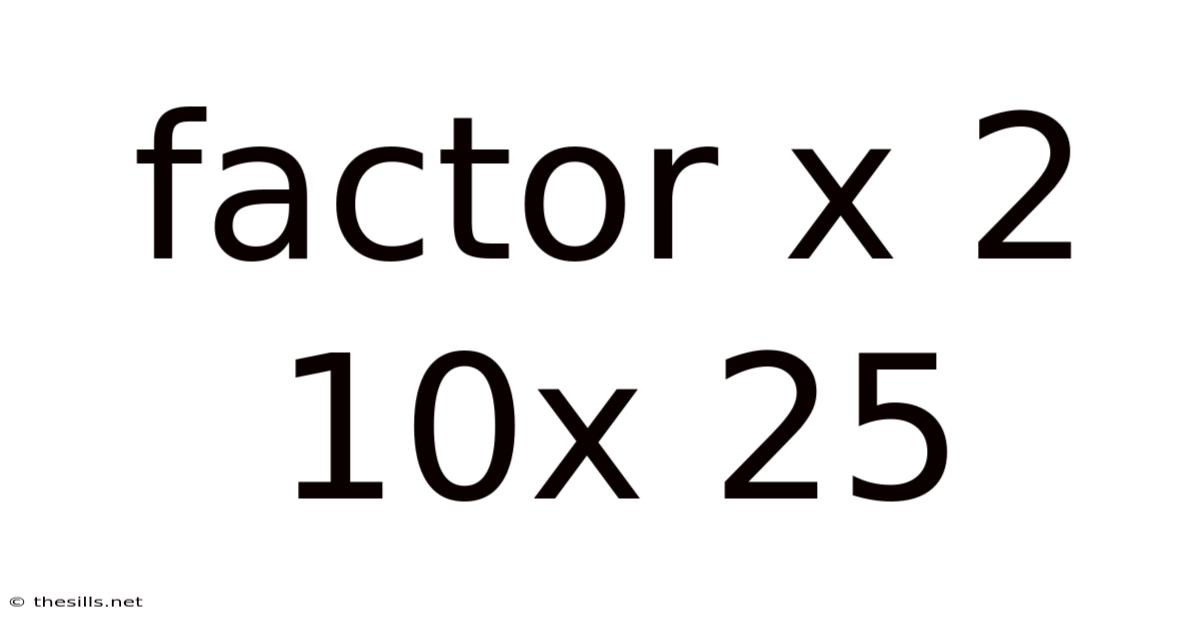
Table of Contents
Unraveling the Mystery: A Deep Dive into the Quadratic Expression x² + 10x + 25
The quadratic expression x² + 10x + 25 might seem deceptively simple at first glance. However, understanding its structure, factorization, and applications reveals a wealth of mathematical concepts crucial for algebra and beyond. This article will explore this expression comprehensively, covering its factorization, graphical representation, real-world applications, and frequently asked questions. By the end, you'll not only understand how to factor it, but also why it's significant in the broader context of mathematics.
Understanding Quadratic Expressions
Before diving into the specifics of x² + 10x + 25, let's establish a foundation. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our expression, x² + 10x + 25, fits this form perfectly, with a = 1, b = 10, and c = 25.
Understanding quadratic expressions is fundamental to many areas of mathematics, including:
- Solving quadratic equations: Setting a quadratic expression equal to zero creates a quadratic equation, which can be solved to find the values of 'x' that make the equation true. These solutions represent the x-intercepts of the parabola when graphed.
- Graphing parabolas: Quadratic expressions represent parabolas, U-shaped curves. Understanding the expression's characteristics helps predict the parabola's shape, vertex, and intercepts.
- Modeling real-world phenomena: Quadratic expressions are used to model various real-world situations, such as projectile motion, area calculations, and optimization problems.
Factoring x² + 10x + 25: The Perfect Square Trinomial
The key to understanding x² + 10x + 25 lies in its factorization. Factoring involves expressing the quadratic expression as a product of simpler expressions. In this case, x² + 10x + 25 is a perfect square trinomial. This means it can be factored into the square of a binomial.
Let's break down the factorization process:
-
Identify the square roots: Notice that x² is the square of x (x * x = x²), and 25 is the square of 5 (5 * 5 = 25).
-
Check the middle term: The middle term, 10x, is twice the product of the square roots we identified. That is, 2 * x * 5 = 10x.
-
Factorization: Because these conditions are met, x² + 10x + 25 can be factored as (x + 5)(x + 5), which simplifies to (x + 5)².
Therefore, the factored form of x² + 10x + 25 is (x + 5)².
Alternative Factoring Methods
While the perfect square trinomial method is the most efficient for this specific expression, let's explore other factoring techniques applicable to quadratic expressions in general:
-
Factoring by grouping: This method is useful when dealing with more complex quadratic expressions. It involves splitting the middle term into two parts and then grouping terms to factor. This method is less straightforward for x² + 10x + 25 but is valuable for learning more general factoring strategies.
-
Quadratic formula: The quadratic formula is a general method for solving quadratic equations (and therefore, implicitly, for factoring). While less intuitive for this specific case, it provides a robust solution for any quadratic expression, regardless of its factorability. The formula is: x = [-b ± √(b² - 4ac)] / 2a. Applying this to our expression would lead to the same solution.
Graphical Representation: The Parabola
The expression x² + 10x + 25 represents a parabola when graphed on a Cartesian plane. Understanding its factored form helps us visualize its key features:
-
Vertex: The vertex of the parabola is the point where the curve reaches its minimum or maximum value. Since our expression is (x + 5)², the vertex lies at (-5, 0). This is because the expression is minimized when x = -5 (resulting in a value of 0).
-
X-intercept: The x-intercept is the point where the parabola intersects the x-axis (where y = 0). Since (x + 5)² = 0, the x-intercept is at x = -5. This is also the vertex in this case because it's a perfect square trinomial.
-
Y-intercept: The y-intercept is the point where the parabola intersects the y-axis (where x = 0). Substituting x = 0 into the expression gives 25, so the y-intercept is at (0, 25).
-
Axis of symmetry: The parabola is symmetrical about a vertical line passing through its vertex. The equation of this line is x = -5.
Real-World Applications
Quadratic expressions, and specifically the ability to factor them, have numerous real-world applications:
-
Projectile motion: The path of a projectile (e.g., a ball thrown into the air) can be modeled using a quadratic equation. Factoring can help determine the time it takes for the projectile to reach the ground.
-
Area calculations: The area of a rectangle with a specific relationship between its sides can be represented by a quadratic expression. Factoring can be used to find the dimensions that result in a given area.
-
Optimization problems: Many optimization problems involve finding the maximum or minimum value of a quadratic function. Factoring can simplify the process of finding these optimal values.
-
Engineering and physics: Quadratic equations appear extensively in engineering and physics problems related to forces, energy, and motion. Understanding how to factor them is critical to solving these problems efficiently.
Frequently Asked Questions (FAQ)
Q: Can all quadratic expressions be factored easily?
A: No, not all quadratic expressions can be easily factored using simple integer factors. Some may require the quadratic formula or other advanced techniques. The expression x² + 10x + 25 is a special case because it's a perfect square trinomial.
Q: What if the coefficient of x² is not 1?
A: If the coefficient of x² is not 1, the factoring process becomes slightly more complex. Techniques like factoring by grouping or using the quadratic formula become more essential.
Q: What is the significance of the discriminant (b² - 4ac)?
A: The discriminant in the quadratic formula (b² - 4ac) determines the nature of the roots (solutions) of the quadratic equation. If the discriminant is positive, there are two distinct real roots. If it's zero, there's one real root (as in our case), and if it's negative, there are two complex roots.
Q: How can I check if my factorization is correct?
A: Expand the factored form back into the original expression. If you get the original expression, your factorization is correct. For example, expanding (x + 5)² gives x² + 10x + 25.
Conclusion
The seemingly simple quadratic expression x² + 10x + 25 offers a rich exploration into the world of algebra. Understanding its factorization as (x + 5)² is crucial not only for solving equations but also for appreciating the graphical representation of the parabola and its applications in numerous real-world scenarios. This exploration provides a solid foundation for tackling more complex quadratic expressions and further developing algebraic skills. Remember, mastering quadratic expressions is a stepping stone to more advanced mathematical concepts, so keep practicing and exploring!
Latest Posts
Latest Posts
-
Factor 2x 2 X 4
Sep 18, 2025
-
Mm Squared To Meters Squared
Sep 18, 2025
-
Mont Blanc By Percy Shelley
Sep 18, 2025
-
How Many Chambers Fish Heart
Sep 18, 2025
-
Integral Of Sin Sqrt X
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 10x 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.