Factor 2x 2 X 4
thesills
Sep 18, 2025 · 6 min read
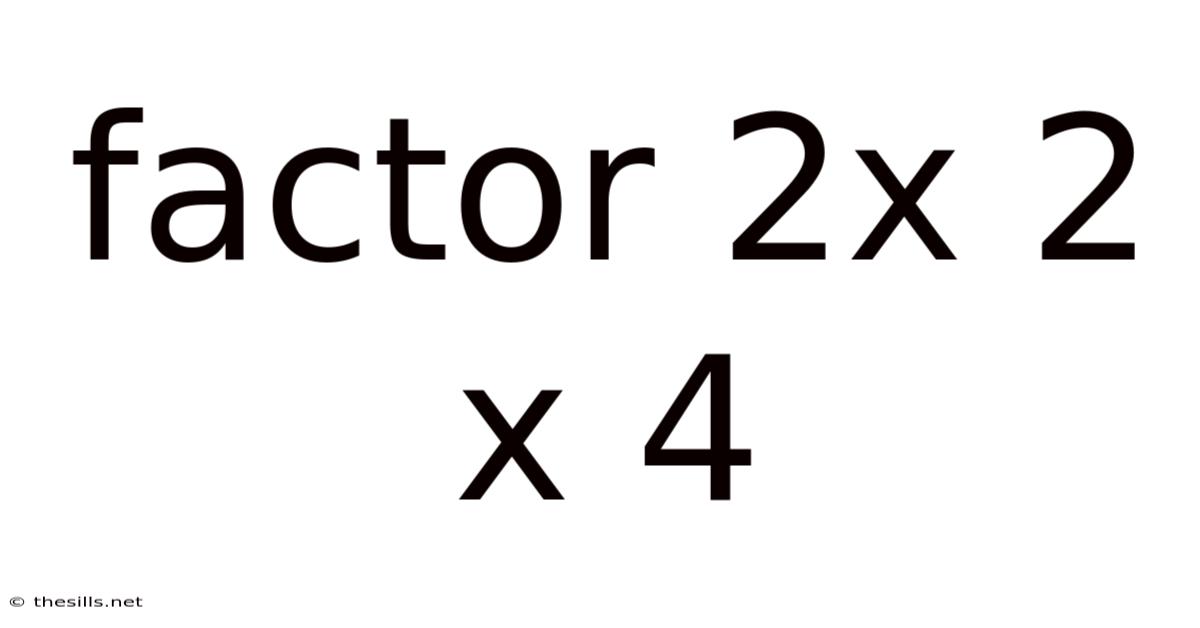
Table of Contents
Decoding 2 x 2 x 4: A Deep Dive into Factorization and its Applications
Understanding the seemingly simple expression "2 x 2 x 4" opens doors to a vast world of mathematical concepts. This seemingly basic calculation acts as a gateway to exploring fundamental principles of factorization, prime numbers, and their significant role in various fields, from cryptography to computer science. This article will explore the factorization of 2 x 2 x 4, delve into its underlying mathematical concepts, and illuminate its broader applications. We'll move beyond the simple arithmetic to understand the why behind the calculation and the power it holds in more complex scenarios.
Understanding the Basics: What is Factorization?
Factorization, also known as factoring, is the process of breaking down a number into smaller numbers that, when multiplied together, give the original number. These smaller numbers are called factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because 1 x 12 = 12, 2 x 6 = 12, and 3 x 4 = 12. The prime factorization of a number involves expressing it as a product of only prime numbers. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Factoring 2 x 2 x 4: A Step-by-Step Approach
The expression "2 x 2 x 4" is already partially factored. However, to achieve the complete prime factorization, we need to break down each factor into its prime components.
-
Step 1: Identify the factors: We have the numbers 2, 2, and 4.
-
Step 2: Find the prime factorization of each factor:
- 2 is already a prime number.
- 2 is already a prime number.
- 4 can be factored as 2 x 2.
-
Step 3: Combine the prime factors: Putting it all together, the prime factorization of 2 x 2 x 4 is 2 x 2 x 2 x 2, which can be written more concisely as 2<sup>4</sup>. This means that 16 (2 x 2 x 2 x 2 = 16) is the product of the expression.
The Significance of Prime Factorization
The prime factorization of a number is unique. This means that every number (except 1) can be expressed as a product of prime numbers in only one way, disregarding the order of the factors. This fundamental property is crucial in many areas of mathematics and computer science.
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization provides an efficient way to find the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
-
Simplifying Fractions: Prime factorization helps simplify fractions to their lowest terms. By finding the prime factors of the numerator and the denominator, we can cancel out common factors, reducing the fraction to its simplest form.
-
Solving Diophantine Equations: These equations involve finding integer solutions to algebraic equations. Prime factorization plays a vital role in solving certain types of Diophantine equations.
-
Cryptography: Prime numbers are the cornerstone of many modern encryption techniques. The difficulty of factoring very large numbers into their prime components forms the basis of the security of these systems. RSA encryption, for instance, relies heavily on this principle. The larger the prime numbers used, the more secure the encryption.
Beyond the Basics: Exploring Related Concepts
Understanding 2 x 2 x 4 allows us to explore more advanced mathematical concepts:
-
Exponents and Powers: The expression 2<sup>4</sup> illustrates the concept of exponents. The base (2) is multiplied by itself the number of times indicated by the exponent (4).
-
Order of Operations (PEMDAS/BODMAS): While this example is straightforward, it highlights the importance of following the order of operations to ensure accurate calculations. Parentheses, exponents, multiplication and division (from left to right), addition and subtraction (from left to right).
-
Number Systems: The numbers involved (2 and 4) are whole numbers, but the concepts of factorization and prime numbers extend to other number systems, such as rational numbers (fractions), real numbers, and complex numbers.
Applications in Real-World Scenarios
The seemingly simple calculation "2 x 2 x 4" has far-reaching applications in various fields:
-
Computer Science: Prime factorization is fundamental to algorithms used in cryptography and data compression.
-
Engineering: Engineers use factorization in calculations related to structural design, circuit analysis, and signal processing.
-
Finance: Factorization principles are applied in financial modeling and risk assessment.
-
Physics: Many physical phenomena can be modeled using mathematical equations that involve factorization.
-
Chemistry: Stoichiometry, the study of quantitative relationships in chemical reactions, relies on understanding ratios and proportions, concepts closely linked to factorization.
Frequently Asked Questions (FAQ)
Q: What is the difference between a factor and a prime factor?
A: A factor is any number that divides another number without leaving a remainder. A prime factor is a factor that is also a prime number (a number greater than 1 divisible only by 1 and itself). In 2 x 2 x 4, 2 and 4 are factors, but only 2 is a prime factor.
Q: Why is prime factorization important in cryptography?
A: The difficulty of factoring very large numbers into their prime components is the foundation of many modern encryption techniques. It's computationally very intensive to factor extremely large numbers, making it secure. Breaking the encryption would require factoring these enormous numbers, which is currently impractical.
Q: Can any number be factored into prime numbers?
A: Yes, every whole number greater than 1 can be uniquely factored into prime numbers (Fundamental Theorem of Arithmetic).
Q: How can I find the prime factorization of a larger number?
A: There are several methods, including trial division (dividing by successively larger prime numbers), factor trees, and more sophisticated algorithms for very large numbers.
Conclusion: The Power of Simplicity
The seemingly simple calculation 2 x 2 x 4 unveils a wealth of mathematical concepts with profound implications. Understanding its prime factorization (2<sup>4</sup>) is not just about arithmetic; it's a stepping stone to grasping the fundamental principles of number theory, which underpin many advanced mathematical and computational processes. From cryptography to engineering, the power of factorization extends far beyond the initial calculation, highlighting the beauty and utility of even the most basic mathematical concepts. The seemingly simple act of factoring provides a gateway to understanding the intricate workings of the mathematical universe and its far-reaching impact on our world. By understanding the principles behind this simple calculation, we unlock a deeper appreciation for the elegance and power of mathematics.
Latest Posts
Latest Posts
-
What Is A Rationalizing Factor
Sep 18, 2025
-
What Is An Ohmic Device
Sep 18, 2025
-
What Did Griffiths Experiment Show
Sep 18, 2025
-
11 73 As A Decimal
Sep 18, 2025
-
9 2 Arrangement Of Microtubules
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.