F X 2 X 2
thesills
Sep 13, 2025 · 7 min read
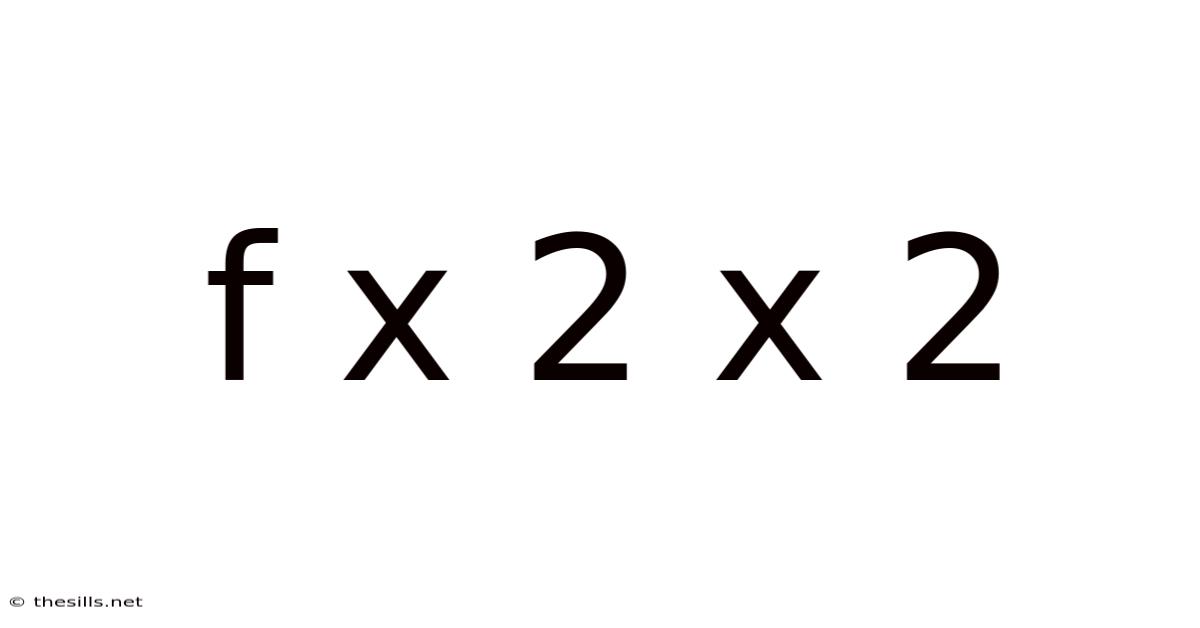
Table of Contents
Delving Deep into f(x) = 2x²: A Comprehensive Exploration
Understanding quadratic functions is fundamental to a solid grasp of algebra and calculus. This article provides a comprehensive exploration of the function f(x) = 2x², covering its properties, graphical representation, transformations, applications, and related concepts. Whether you're a high school student grappling with algebra or a more advanced learner revisiting foundational concepts, this in-depth guide will equip you with a thorough understanding of this crucial function.
Introduction: Understanding the Basics of f(x) = 2x²
The function f(x) = 2x² is a simple yet powerful example of a quadratic function. A quadratic function is a polynomial function of degree two, meaning the highest power of the variable x is 2. The general form of a quadratic function is f(x) = ax² + bx + c, where a, b, and c are constants, and a ≠ 0. In our case, f(x) = 2x², we have a = 2, b = 0, and c = 0. This specific form allows for a clear illustration of fundamental quadratic properties without the complexities introduced by non-zero b and c values. We'll explore how these constants influence the graph and behavior of the function.
Graphical Representation and Key Features
The graph of f(x) = 2x² is a parabola. Parabolas are symmetrical U-shaped curves. The key features to identify are:
-
Vertex: The vertex is the lowest (or highest, for functions with a negative leading coefficient) point on the parabola. For f(x) = 2x², the vertex is at the origin (0, 0). This is because the function is in its simplest form, without any vertical or horizontal shifts.
-
Axis of Symmetry: This is a vertical line that divides the parabola into two mirror images. For f(x) = 2x², the axis of symmetry is the y-axis (x = 0).
-
Concavity: The parabola opens upwards because the coefficient of x² (a = 2) is positive. If 'a' were negative, the parabola would open downwards.
-
x-intercept(s): These are the points where the graph intersects the x-axis (where y = 0). For f(x) = 2x², the only x-intercept is at (0, 0). Solving 2x² = 0 gives x = 0.
-
y-intercept: This is the point where the graph intersects the y-axis (where x = 0). For f(x) = 2x², the y-intercept is at (0, 0). Substituting x = 0 into the function gives f(0) = 0.
-
Rate of Change: The steepness of the parabola is determined by the value of 'a'. A larger value of 'a' (like our 2) results in a narrower, steeper parabola. A smaller positive value of 'a' would result in a wider, flatter parabola.
Transformations of f(x) = 2x²
Understanding how transformations affect the basic parabola is crucial. We can modify f(x) = 2x² by applying various transformations:
-
Vertical Shifts: Adding a constant 'k' to the function shifts the parabola vertically. f(x) = 2x² + k shifts the parabola upwards by 'k' units if k is positive and downwards by 'k' units if k is negative.
-
Horizontal Shifts: Replacing 'x' with (x - h) shifts the parabola horizontally. f(x) = 2(x - h)² shifts the parabola to the right by 'h' units if h is positive and to the left by 'h' units if h is negative.
-
Vertical Stretches/Compressions: Multiplying the function by a constant 'a' (in our case, already 2) stretches or compresses the parabola vertically. A value of |a| > 1 stretches the parabola vertically, making it narrower, while 0 < |a| < 1 compresses it vertically, making it wider.
-
Reflections: Multiplying the function by -1 reflects the parabola across the x-axis. f(x) = -2x² would be a downward-opening parabola.
Solving Equations and Inequalities Involving f(x) = 2x²
Solving equations and inequalities involving f(x) = 2x² often involves applying algebraic techniques:
-
Solving Equations: To solve an equation like 2x² = 8, divide both sides by 2 to get x² = 4. Then, take the square root of both sides, remembering to consider both positive and negative solutions: x = ±2.
-
Solving Inequalities: To solve an inequality like 2x² > 8, follow the same steps as above, but consider the inequality sign. Dividing by 2 gives x² > 4. This means x > 2 or x < -2.
Calculus Applications: Derivatives and Integrals
The function f(x) = 2x² provides a simple yet illustrative example for applying calculus concepts:
-
Derivative: The derivative of f(x) = 2x² represents the instantaneous rate of change of the function at any point x. Using the power rule of differentiation, the derivative f'(x) = 4x. This means the slope of the tangent line to the parabola at any point x is 4x.
-
Integral: The definite integral of f(x) = 2x² over an interval [a, b] represents the area under the curve between x = a and x = b. Using the power rule of integration, the indefinite integral is F(x) = (2/3)x³ + C, where C is the constant of integration. The definite integral from a to b is (2/3)b³ - (2/3)a³.
Real-World Applications
Quadratic functions, like f(x) = 2x², have numerous applications in various fields:
-
Physics: Projectile motion is often modeled using quadratic functions. The height of a projectile launched vertically can be expressed as a quadratic function of time.
-
Engineering: The shape of a parabolic antenna is described by a quadratic function, allowing for efficient focusing of radio waves.
-
Economics: Quadratic functions can be used to model cost, revenue, and profit functions in business.
-
Computer Graphics: Parabolas and quadratic curves are essential elements in computer graphics and animation for creating smooth, curved shapes.
Further Exploration: Extending the Concepts
Understanding f(x) = 2x² serves as a foundation for exploring more complex quadratic functions and related concepts:
-
Completing the Square: This technique is used to rewrite quadratic functions in vertex form, revealing the vertex and axis of symmetry more easily.
-
Quadratic Formula: This formula provides a direct way to find the roots (x-intercepts) of any quadratic equation, even those that cannot be easily factored.
-
Discriminant: The discriminant of a quadratic equation (b² - 4ac) determines the nature of the roots (real and distinct, real and equal, or complex).
-
Parabola Properties: Investigating properties like the focus, directrix, and latus rectum of a parabola provides deeper insights into its geometric characteristics.
Frequently Asked Questions (FAQ)
Q: What is the domain and range of f(x) = 2x²?
A: The domain of f(x) = 2x² is all real numbers (-∞, ∞) because you can input any real number for x. The range is [0, ∞), meaning the output (y-values) are always greater than or equal to zero because the parabola opens upwards.
Q: How does the coefficient '2' affect the graph?
A: The coefficient '2' stretches the parabola vertically, making it narrower than the basic parabola y = x². It increases the rate at which the function's output increases as x increases.
Q: Can f(x) = 2x² be factored?
A: Yes, it can be factored as 2x². This shows that the only root is x=0.
Q: What is the inverse function of f(x) = 2x²?
A: A true inverse function requires a one-to-one relationship. Since f(x) = 2x² is not one-to-one (it fails the horizontal line test), it doesn't have a true inverse function over its entire domain. However, a restricted inverse function can be defined for x ≥ 0, which would be f⁻¹(x) = √(x/2).
Conclusion: Mastering f(x) = 2x² and Beyond
The seemingly simple function f(x) = 2x² provides a rich foundation for understanding quadratic functions, their graphical representation, transformations, and applications. By mastering this function and the concepts discussed, you build a strong base for tackling more advanced mathematical concepts in algebra, calculus, and various applied fields. Remember that consistent practice and a deep understanding of the underlying principles are key to achieving proficiency in mathematics. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
Ejection Fraction Vs Stroke Volume
Sep 13, 2025
-
Is 3 4 And 6 8 Equivalent
Sep 13, 2025
-
All Equilateral Triangles Are Isosceles
Sep 13, 2025
-
How To Calculate Q Value
Sep 13, 2025
-
Factor 6x 2 5x 6
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about F X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.