4x 2 4x 3 Factor
thesills
Sep 14, 2025 · 6 min read
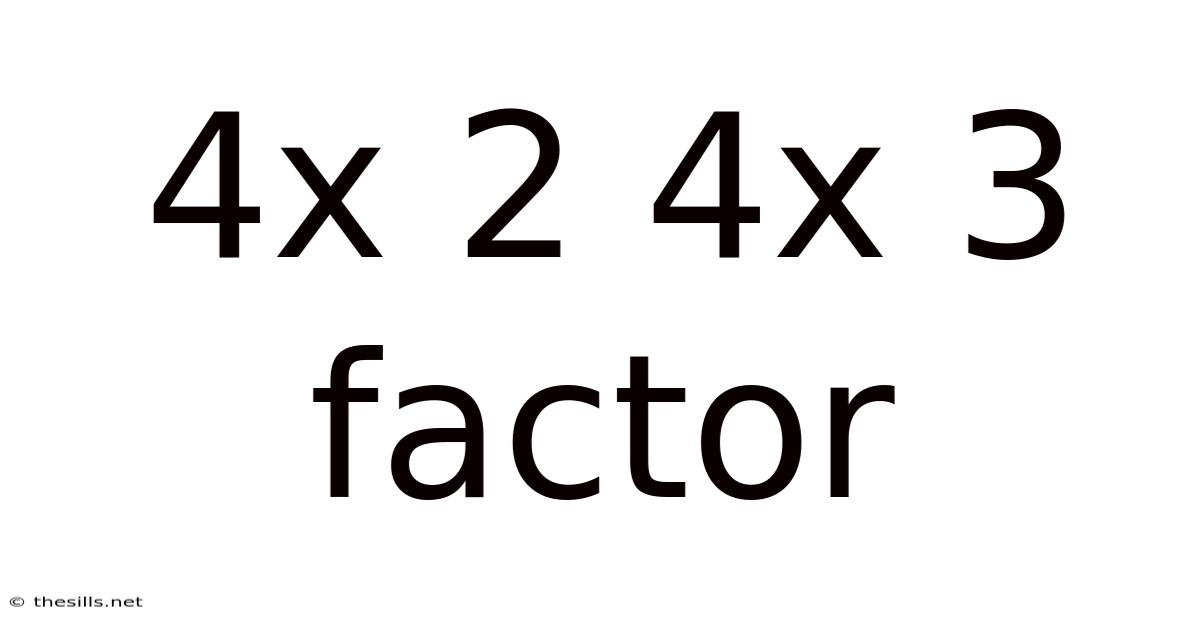
Table of Contents
Understanding and Mastering the 4x2 and 4x3 Factor: A Comprehensive Guide
The terms "4x2 factor" and "4x3 factor" aren't standard mathematical or scientific notations. They lack established definitions within conventional fields like algebra, statistics, or engineering. It's likely these terms are used within a specific context, possibly an industry-specific application, a specialized software program, or even a colloquialism within a particular community. Without knowing the source or context where you encountered these terms, providing a precise and definitive explanation is impossible.
However, we can approach this topic by exploring possible interpretations and providing a comprehensive guide on how to analyze and understand similar concepts in different fields. This will equip you with the tools to decipher the meaning of "4x2" and "4x3" factors should you encounter them in the future, regardless of their specific application.
Possible Interpretations and Analogous Concepts
Let's examine several areas where similar notations could appear, providing illustrative examples and explanatory context.
1. Matrix Algebra and Linear Transformations:
In linear algebra, "4x2" and "4x3" could represent the dimensions of matrices. A 4x2 matrix has 4 rows and 2 columns, while a 4x3 matrix has 4 rows and 3 columns. These matrices are fundamental tools in various applications:
- Image Processing: Matrices can represent images, where each element represents a pixel's color value. A 4x2 matrix could represent a small, rectangular image.
- Data Analysis: Matrices are used to organize and manipulate data sets. A 4x3 matrix might represent four observations of three different variables.
- Linear Transformations: Matrices can perform transformations on vectors, such as rotation, scaling, or shearing. The dimensions of the matrix determine the type and effect of the transformation.
Example of a 4x2 Matrix:
[ 1 2 ]
[ 3 4 ]
[ 5 6 ]
[ 7 8 ]
Example of a 4x3 Matrix:
[ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
[10 11 12 ]
Operations with Matrices: Matrix multiplication, addition, and other operations are defined based on their dimensions. Understanding these operations is crucial for working with 4x2 and 4x3 matrices. For instance, multiplying a 4x2 matrix by a 2x3 matrix results in a 4x3 matrix. However, multiplying a 4x2 matrix by a 4x3 matrix is not defined.
2. Factorial Design in Experimental Design:
In experimental design, "4x2" and "4x3" could denote a factorial design. This involves investigating the effects of multiple factors (independent variables) on a response variable. The numbers represent the number of levels for each factor.
- 4x2 Factorial Design: This design has one factor with 4 levels and another factor with 2 levels. It requires conducting 4 * 2 = 8 experiments.
- 4x3 Factorial Design: This design has one factor with 4 levels and another factor with 3 levels, requiring 4 * 3 = 12 experiments.
These designs allow researchers to investigate main effects (the individual effects of each factor) and interaction effects (how the factors affect each other). Analyzing the results of such experiments involves statistical methods like ANOVA (Analysis of Variance).
3. Engineering and Design Specifications:
In engineering and product design, "4x2" and "4x3" could refer to physical dimensions or configurations. This is highly context-dependent; for instance:
- Dimensions: It might refer to the dimensions of a component (e.g., 4 units wide by 2 units high). The units would need to be specified (inches, centimeters, etc.).
- Array Configuration: It might describe an arrangement of elements, like a grid of 4 rows and 2 columns of sensors or components.
4. Programming and Data Structures:
In programming, "4x2" and "4x3" could describe arrays or data structures.
- Arrays: Similar to matrices, arrays can be 2-dimensional, representing data with rows and columns.
- Data Structures: More complex data structures, like trees or graphs, might utilize these numbers to define aspects of their organization.
5. Other Specialized Contexts:
The meanings of "4x2 factor" and "4x3 factor" could be unique to a specific field or application. Without further context, it's impossible to provide a more precise definition. Consider looking for clues in the surrounding text or documentation where you encountered these terms.
Understanding Factorial Design: A Deeper Dive
Let's elaborate on factorial designs, as they represent a common use of numerical combinations that might be represented by notations similar to "4x2" and "4x3."
Factorial designs are experimental designs that allow researchers to study the effects of multiple factors (independent variables) on a response variable (dependent variable). They are particularly useful when investigating interactions between factors. In a factorial design, each level of one factor is combined with each level of the other factor(s).
Types of Factorial Designs:
- 2-level Factorial Designs: These designs have only two levels for each factor (e.g., high and low, presence and absence). They are simpler to analyze but might lack the detail needed to capture complex relationships.
- Multi-level Factorial Designs: These designs have more than two levels for at least one factor. They provide a more nuanced understanding of the factors' effects but require more experimental runs and more complex analysis. Our "4x2" and "4x3" examples fall into this category.
Advantages of Factorial Designs:
- Efficiency: Factorial designs are more efficient than conducting separate experiments for each factor. They provide more information with fewer experimental runs.
- Interaction Effects: Factorial designs can detect interaction effects, which are crucial for understanding how factors influence each other.
- Generalizability: Well-designed factorial experiments allow for better generalization of the results to broader populations and conditions.
Analyzing Factorial Designs:
Analyzing factorial design experiments typically involves statistical techniques like ANOVA (Analysis of Variance) or regression analysis. These methods help to determine:
- Main effects: The individual effects of each factor.
- Interaction effects: How the factors interact with each other.
Example of a 2x3 Factorial Design:
Let's say we are testing the effect of fertilizer type (Factor A: two levels – Organic and Chemical) and watering frequency (Factor B: three levels – Daily, Every Other Day, Weekly) on plant growth (response variable). This is a 2x3 factorial design.
The experiment would involve 2 * 3 = 6 different experimental conditions:
- Organic fertilizer, daily watering
- Organic fertilizer, every other day watering
- Organic fertilizer, weekly watering
- Chemical fertilizer, daily watering
- Chemical fertilizer, every other day watering
- Chemical fertilizer, weekly watering
Each condition would be replicated several times to account for random variation. The data collected would then be analyzed using ANOVA to determine the effects of fertilizer type, watering frequency, and their interaction on plant growth.
Conclusion:
The meaning of "4x2 factor" and "4x3 factor" remains ambiguous without knowing the context in which they were used. However, by exploring analogous concepts in linear algebra, experimental design, engineering, and programming, we have developed a deeper understanding of potential interpretations. This demonstrates the importance of contextual awareness when interpreting specialized notations. By examining the surrounding information and the field of application, you'll be better equipped to decipher the meaning of similar terms in the future. Remember that clear communication and well-defined terminology are crucial for effective collaboration and understanding in any field.
Latest Posts
Latest Posts
-
How To Make Paper Transparent
Sep 14, 2025
-
2x 3 3x 7 0
Sep 14, 2025
-
Molar Mass Of Sulphuric Acid
Sep 14, 2025
-
4 7 8 To Decimal
Sep 14, 2025
-
Ph Of Ba Oh 2
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4x 2 4x 3 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.