30/7 As A Mixed Number
thesills
Sep 18, 2025 · 6 min read
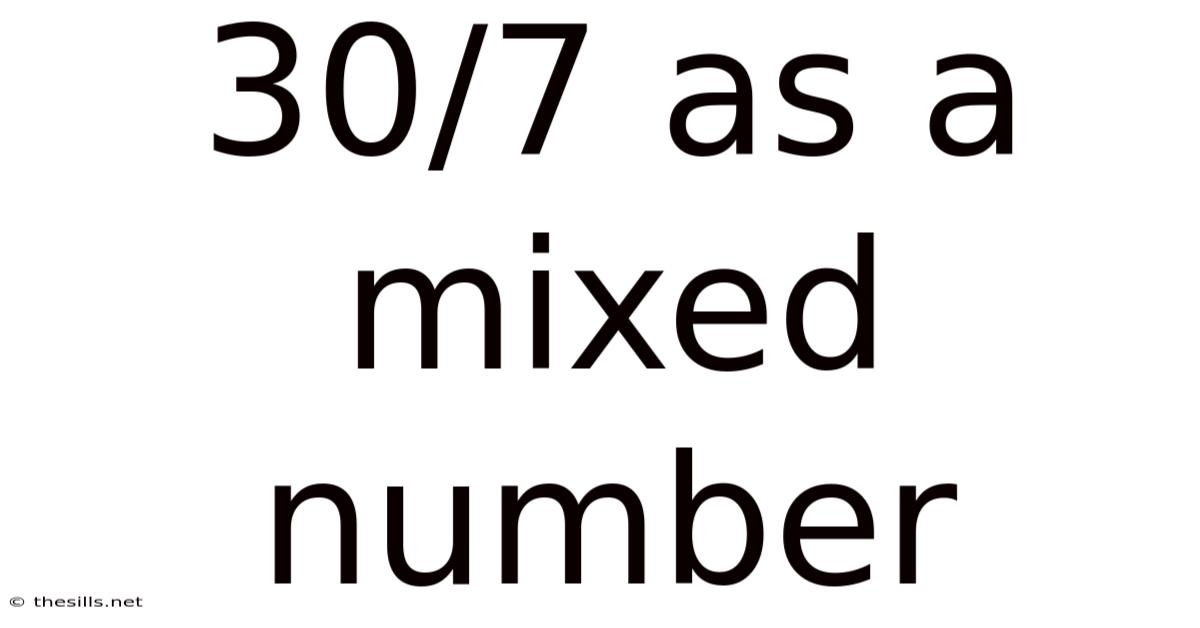
Table of Contents
Understanding 30/7 as a Mixed Number: A Comprehensive Guide
The concept of mixed numbers is fundamental in arithmetic and forms the basis for more advanced mathematical concepts. This article will provide a thorough understanding of how to convert an improper fraction, like 30/7, into a mixed number, exploring the underlying principles and providing practical examples. We'll also address frequently asked questions and delve into the practical applications of this conversion. Understanding mixed numbers is crucial for various mathematical operations and real-world problem-solving.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number), like 1/2, 3/4, or 5/8. For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit. Mixed numbers are commonly used to represent quantities that are more than one whole but less than the next whole number.
Converting an Improper Fraction to a Mixed Number
An improper fraction is a fraction where the numerator is greater than or equal to the denominator, such as 30/7. To convert an improper fraction to a mixed number, we need to determine how many whole units are contained within the fraction and what fraction remains. This process involves division.
Let's work through the conversion of 30/7:
-
Divide the numerator by the denominator: We divide 30 by 7.
30 ÷ 7 = 4 with a remainder of 2.
-
The quotient becomes the whole number: The quotient, 4, represents the whole number part of our mixed number.
-
The remainder becomes the numerator of the proper fraction: The remainder, 2, becomes the numerator of the fraction.
-
The denominator remains the same: The denominator of the fraction remains 7.
Therefore, 30/7 as a mixed number is 4 2/7.
Step-by-Step Guide with Examples
Let's reinforce this process with a few more examples:
Example 1: Converting 17/5 to a mixed number
- Divide 17 by 5: 17 ÷ 5 = 3 with a remainder of 2.
- The whole number is 3.
- The remainder is 2, becoming the new numerator.
- The denominator remains 5.
Therefore, 17/5 = 3 2/5.
Example 2: Converting 22/3 to a mixed number
- Divide 22 by 3: 22 ÷ 3 = 7 with a remainder of 1.
- The whole number is 7.
- The remainder is 1, becoming the new numerator.
- The denominator remains 3.
Therefore, 22/3 = 7 1/3.
Example 3: Converting 15/4 to a mixed number
- Divide 15 by 4: 15 ÷ 4 = 3 with a remainder of 3.
- The whole number is 3.
- The remainder is 3, becoming the new numerator.
- The denominator remains 4.
Therefore, 15/4 = 3 3/4.
These examples demonstrate the consistent application of the division method to transform improper fractions into their mixed number equivalents.
The Mathematical Rationale Behind the Conversion
The conversion from an improper fraction to a mixed number is fundamentally based on the concept of dividing a quantity into equal parts. The improper fraction represents a quantity that exceeds one whole unit. By dividing the numerator by the denominator, we determine how many complete units are present and the remaining portion, which is represented as a proper fraction.
For instance, in 30/7, we're dividing 30 items into groups of 7. We can form 4 complete groups (4 x 7 = 28), and we have 2 items remaining (30 - 28 = 2). These 2 remaining items represent 2/7 of another group. Hence, we have 4 whole groups and 2/7 of another group, resulting in the mixed number 4 2/7.
Converting a Mixed Number Back to an Improper Fraction
It's important to understand the reverse process as well. To convert a mixed number back to an improper fraction:
- Multiply the whole number by the denominator: For example, in 4 2/7, multiply 4 by 7 (4 x 7 = 28).
- Add the numerator to the result: Add the numerator, 2, to the result from step 1 (28 + 2 = 30).
- Keep the denominator the same: The denominator remains 7.
Therefore, 4 2/7 becomes 30/7. This demonstrates the reversibility of the conversion process.
Real-World Applications of Mixed Numbers
Mixed numbers find practical applications in numerous everyday situations:
- Measurement: Expressing lengths (e.g., 2 1/2 feet), weights (e.g., 3 3/4 pounds), or volumes (e.g., 1 1/2 liters).
- Cooking and Baking: Following recipes that require quantities like 1 1/4 cups of flour or 2 1/2 teaspoons of sugar.
- Time: Representing durations such as 1 hour and 15 minutes (1 1/4 hours).
- Construction and Engineering: Calculations involving dimensions and quantities.
- Data Analysis: Presenting data in a more easily understandable format.
Frequently Asked Questions (FAQ)
Q1: What if the remainder is 0 after the division?
A1: If the remainder is 0, it means the improper fraction is a whole number. For example, 28/7 = 4 (since 28 ÷ 7 = 4 with no remainder). There is no fractional part in the mixed number.
Q2: Can I convert any fraction to a mixed number?
A2: No, only improper fractions (where the numerator is greater than or equal to the denominator) can be converted to mixed numbers. Proper fractions already represent a part of a whole and cannot be expressed as a whole number plus a fraction.
Q3: Are there different ways to represent the same quantity using fractions and mixed numbers?
A3: Yes, the same quantity can be expressed in multiple ways. For example, 30/7, 4 2/7, and even as a decimal (approximately 4.286) all represent the same numerical value. The choice of representation depends on the context and the desired level of precision.
Q4: Why are mixed numbers important in everyday life?
A4: Mixed numbers are crucial for representing quantities in a user-friendly manner. Using a mixed number like 2 1/2 feet is more intuitive and understandable than using the equivalent improper fraction, 5/2 feet, particularly in everyday communication and practical applications.
Conclusion
Converting an improper fraction, such as 30/7, to a mixed number (4 2/7) is a fundamental skill in mathematics with practical implications across many fields. Understanding the process, which involves division and the interpretation of the quotient and remainder, empowers one to handle real-world situations involving fractional quantities efficiently. The ability to confidently convert between improper fractions and mixed numbers provides a robust foundation for further mathematical learning and problem-solving. The flexibility of using either an improper fraction or a mixed number allows for choosing the most appropriate representation depending on the context, enhancing clarity and practicality in diverse applications.
Latest Posts
Latest Posts
-
20 35 In Lowest Terms
Sep 18, 2025
-
2 Methyl 1 3 Butadiene
Sep 18, 2025
-
What Is Malleability And Ductility
Sep 18, 2025
-
Fermentation Of Milk To Yogurt
Sep 18, 2025
-
Integration Of Sin Inverse X
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 30/7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.