3 X 5 X 5
thesills
Sep 12, 2025 · 5 min read
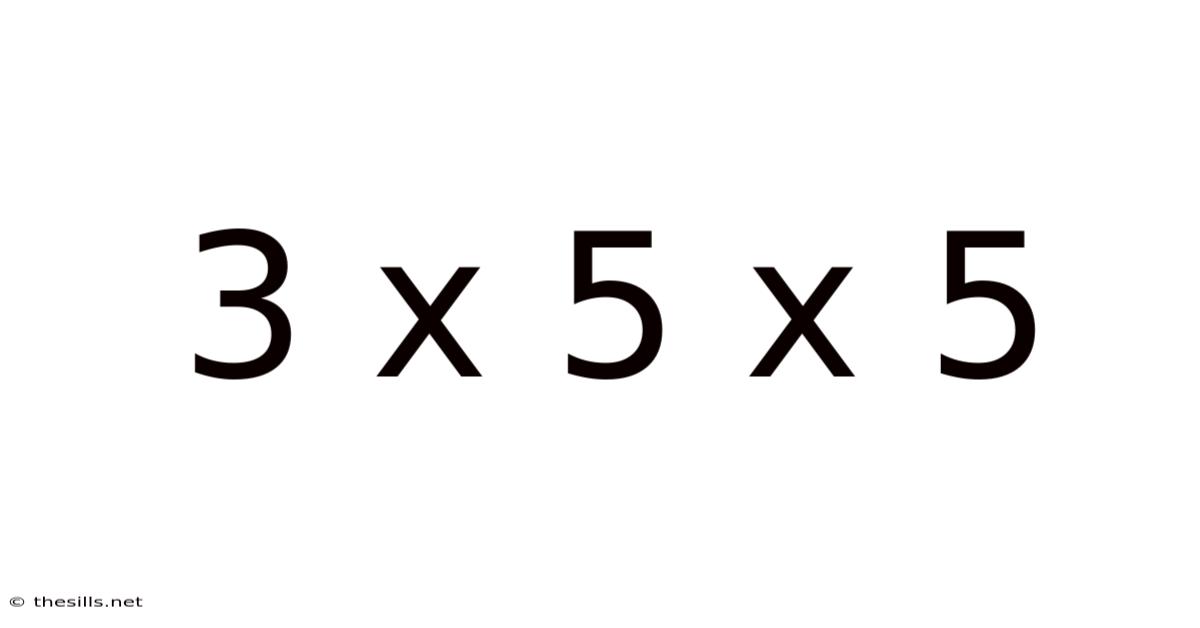
Table of Contents
Decoding 3 x 5 x 5: A Deep Dive into a Simple Calculation and its Broader Implications
The seemingly simple calculation 3 x 5 x 5 might appear trivial at first glance. However, this seemingly innocuous equation opens doors to explore various mathematical concepts, real-world applications, and even philosophical considerations about the nature of representation and problem-solving. This article will delve deep into the multifaceted nature of this calculation, exploring its mathematical underpinnings, practical applications, and expanding on its potential for deeper understanding.
Understanding the Basics: Multiplication and Order of Operations
At its core, 3 x 5 x 5 is a multiplication problem. Multiplication is a fundamental arithmetic operation representing repeated addition. In this case, we are multiplying three numbers: 3, 5, and 5. The order in which we perform these multiplications doesn't affect the final result, thanks to the commutative and associative properties of multiplication.
-
Commutative Property: The order of the numbers doesn't matter (a x b = b x a). Therefore, 3 x 5 x 5 is the same as 5 x 3 x 5, 5 x 5 x 3, and so on.
-
Associative Property: The grouping of the numbers doesn't matter ((a x b) x c = a x (b x c)). We can calculate (3 x 5) x 5 or 3 x (5 x 5) and arrive at the same answer.
Calculating the Result:
Regardless of the order or grouping, the calculation is straightforward:
- Step 1: 3 x 5 = 15
- Step 2: 15 x 5 = 75
Therefore, 3 x 5 x 5 = 75
Beyond the Calculation: Real-World Applications
While seemingly simple, the concept of multiplication, exemplified by 3 x 5 x 5, underpins numerous real-world scenarios. Consider these examples:
-
Area Calculation: Imagine a rectangular prism (like a box). If the dimensions are 3 units long, 5 units wide, and 5 units high, then calculating the volume involves multiplying these three dimensions: 3 x 5 x 5 = 75 cubic units. This concept extends to various fields like construction, packaging, and even urban planning where volume calculations are crucial.
-
Cost Calculation: Suppose you're buying items. If you need 3 sets of items, with each set containing 5 items costing $5 each, the total cost would be 3 x 5 x $5 = $75. This simple calculation is used daily in various shopping scenarios, from groceries to large purchases.
-
Data Representation: In computer science, the concept of dimensions is fundamental. A 3 x 5 x 5 array could represent a three-dimensional dataset, such as a collection of sensor readings or image pixel data. Understanding how to manipulate and process such data structures is vital in various fields like image processing, data analysis, and machine learning.
-
Combinatorics and Probability: The calculation could represent a combinatorial problem. Imagine choosing 3 items from a set of 5 items, and then independently choosing another 5 items from a different set of 5. While not directly represented by 3 x 5 x 5 in this specific combinatorial example, the multiplicative nature highlights the principle of independent choices.
Exploring Mathematical Extensions: Prime Factorization and Exponents
Let's move beyond the simple calculation and explore some related mathematical concepts:
-
Prime Factorization: The number 75 can be broken down into its prime factors. Prime factorization is the process of expressing a number as a product of its prime factors (numbers only divisible by 1 and themselves). The prime factorization of 75 is 3 x 5 x 5 or 3 x 5². Understanding prime factorization is crucial in various mathematical fields like cryptography and number theory.
-
Exponents: The prime factorization shows the use of exponents. The expression 3 x 5² indicates that 5 is multiplied by itself twice. Exponents simplify the representation of repeated multiplication, making complex calculations easier to manage.
Connecting to Larger Concepts: Scaling and Proportionality
The calculation 3 x 5 x 5 demonstrates the fundamental concept of scaling. If we were to double one of the dimensions (e.g., making it 6 x 5 x 5), the result would also double (150). This illustrates the principle of proportionality, where a change in one variable proportionally affects the outcome. This is a cornerstone concept in physics, engineering, and many other fields.
The Philosophical Dimension: Abstraction and Representation
The simple equation 3 x 5 x 5 is not just a mathematical problem; it is a representation. The numbers 3, 5, and 5 can represent various quantities in different contexts. This ability to abstract and represent real-world scenarios using mathematical symbols is a powerful tool for understanding and solving problems. The act of translating a real-world problem into a mathematical equation, solving it, and then interpreting the result back into the real world highlights the power of abstract thinking.
Frequently Asked Questions (FAQ)
Q: What is the order of operations in 3 x 5 x 5?
A: The order of operations doesn't strictly matter in this case due to the commutative and associative properties of multiplication. You can multiply in any order and still get the same result.
Q: Can this calculation be solved using different methods?
A: Yes, besides direct multiplication, you could use different approaches like using a calculator or breaking down the numbers into simpler components before multiplying.
Q: What are some real-world applications beyond those mentioned?
A: The concept of multiplication applies to numerous fields including finance (compound interest), recipe scaling, and even aspects of game design and physics simulations.
Q: Is there a connection to geometry beyond volume calculations?
A: Yes, the numbers could represent coordinates in a three-dimensional space, or the sides of different geometric shapes.
Conclusion: The Unassuming Power of 3 x 5 x 5
The seemingly simple calculation 3 x 5 x 5 serves as a gateway to explore a wide range of mathematical concepts, real-world applications, and abstract thinking. From its fundamental role in arithmetic to its applications in geometry, data representation, and even philosophical discussions about abstraction, this equation showcases the power and versatility of mathematics. By understanding the underlying principles and exploring its connections to other fields, we can appreciate the depth and significance hidden within seemingly simple calculations. The number 75, therefore, represents not just a numerical result, but a symbol of the interconnectedness of various mathematical concepts and their relevance to our everyday lives. This exploration encourages a deeper appreciation for the beauty and utility of mathematics, showing how seemingly simple concepts can lay the foundation for a far broader understanding of the world around us.
Latest Posts
Latest Posts
-
Ethyl Alcohol And Acetic Acid
Sep 12, 2025
-
What Is 4 Of 900
Sep 12, 2025
-
Sodium Hydroxide And Potassium Hydroxide
Sep 12, 2025
-
Factor X 2 X 56
Sep 12, 2025
-
Is Distilled Water An Acid
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 X 5 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.