3 1/8 As A Decimal
thesills
Sep 16, 2025 · 5 min read
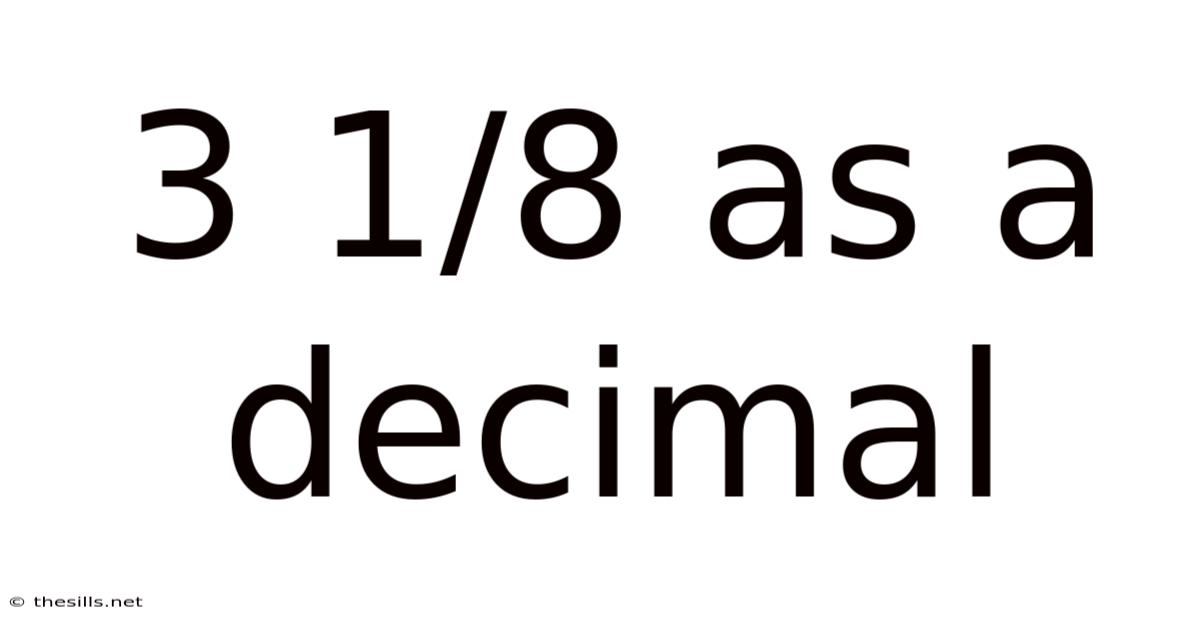
Table of Contents
3 1/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 3 1/8 into its decimal equivalent, explaining the underlying principles and providing additional insights to enhance your understanding of fractions and decimals. We'll cover various methods, address common misconceptions, and answer frequently asked questions to ensure you master this concept.
Understanding Fractions and Decimals
Before diving into the conversion, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/8, 1 is the numerator and 8 is the denominator. This indicates one part out of eight equal parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals are written using a decimal point (.) to separate the whole number part from the fractional part. For example, 0.5 is equivalent to 1/2, and 0.25 is equivalent to 1/4.
Method 1: Converting the Fraction to a Decimal
The mixed number 3 1/8 consists of a whole number (3) and a fraction (1/8). To convert this to a decimal, we first focus on the fractional part. We need to convert the fraction 1/8 into its decimal equivalent. This can be done by dividing the numerator (1) by the denominator (8):
1 ÷ 8 = 0.125
Therefore, the fraction 1/8 is equal to 0.125.
Now, we can combine this decimal with the whole number part:
3 + 0.125 = 3.125
Therefore, 3 1/8 as a decimal is 3.125.
Method 2: Converting to an Improper Fraction First
Another approach is to first convert the mixed number 3 1/8 into an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. To do this:
- Multiply the whole number by the denominator: 3 * 8 = 24
- Add the numerator: 24 + 1 = 25
- Keep the same denominator: 25/8
Now, we have the improper fraction 25/8. We can then convert this improper fraction to a decimal by dividing the numerator by the denominator:
25 ÷ 8 = 3.125
This confirms that 3 1/8 as a decimal is 3.125.
Understanding the Decimal Places
The decimal 3.125 has three digits after the decimal point. Each digit represents a specific place value:
- 3: Represents the whole number part.
- 1: Represents one-tenth (1/10).
- 2: Represents two-hundredths (2/100).
- 5: Represents five-thousandths (5/1000).
This illustrates the relationship between decimal representation and the fractional components.
Visual Representation
Imagine a pie cut into 8 equal slices. The fraction 1/8 represents one of these slices. If we had three whole pies and one-eighth of another, this would visually represent 3 1/8. Converting this to a decimal helps us express the same quantity in a different format, but the value remains the same.
Practical Applications
Converting fractions to decimals is crucial in various fields:
- Engineering and Science: Many calculations in engineering and scientific fields require precise measurements, often represented in decimal form.
- Finance: Calculating interest, discounts, and other financial transactions often involves working with decimal numbers.
- Computer Science: Computers work with binary numbers (0s and 1s), but often represent these values as decimals for easier human understanding.
- Everyday Life: Many everyday situations, such as measuring ingredients for cooking or calculating distances, involve working with fractions and decimals.
Common Misconceptions
A common mistake is incorrectly dividing the whole number by the denominator. Remember, you must only divide the numerator by the denominator to get the decimal equivalent of the fraction. The whole number remains separate until the final addition step.
Another common error is misinterpreting the place value of digits after the decimal point. Understanding the place value system (tenths, hundredths, thousandths, etc.) is critical for accurately interpreting and using decimals.
Further Exploration: Converting Other Fractions to Decimals
The same principles apply to converting other fractions to decimals. For example:
- 1/4: 1 ÷ 4 = 0.25
- 3/5: 3 ÷ 5 = 0.6
- 7/10: 7 ÷ 10 = 0.7
Remember, if the division results in a repeating decimal (e.g., 1/3 = 0.333...), you may need to round the decimal to a specific number of decimal places depending on the context.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals?
A: No, some fractions, like 1/3, result in repeating decimals (0.333...). These are called non-terminating decimals.
Q: What if the fraction has a larger numerator than denominator?
A: If the numerator is larger than the denominator, you have an improper fraction. Convert it to a mixed number first, and then convert the fractional part to a decimal, as demonstrated in Method 2.
Q: How do I convert a decimal back to a fraction?
A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator that is a power of 10 (10, 100, 1000, etc.) depending on the number of digits after the decimal point. Then, simplify the fraction to its lowest terms. For example, 0.75 can be written as 75/100, which simplifies to 3/4.
Q: Why is understanding this conversion important?
A: This skill is fundamental for various mathematical operations and applications in various fields, ensuring a deeper understanding of numbers and their representation.
Conclusion
Converting 3 1/8 to its decimal equivalent, 3.125, highlights the fundamental relationship between fractions and decimals. By understanding the underlying principles and applying the methods explained, you can confidently convert any fraction to its decimal representation and vice versa. This skill is invaluable for various mathematical applications and enhances your overall understanding of numbers. Remember to practice regularly to solidify your understanding and build confidence in tackling similar conversions. The more you practice, the easier and more intuitive this process will become.
Latest Posts
Latest Posts
-
How To Calculate Partial Charge
Sep 16, 2025
-
2 2 4 4 Tetramethylpentane
Sep 16, 2025
-
What Is Shrillness Of Sound
Sep 16, 2025
-
Allows Light To Pass Through
Sep 16, 2025
-
X 1 3 X 3
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 1/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.