2x2 + 8x + 6
thesills
Sep 14, 2025 · 7 min read
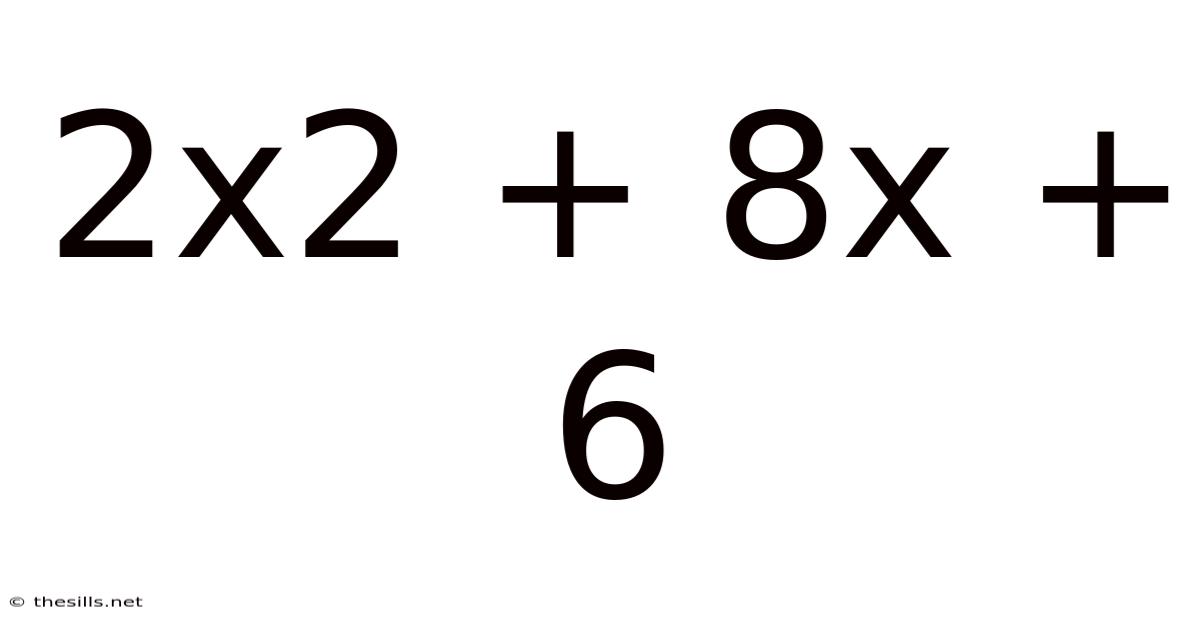
Table of Contents
Decoding the Quadratic Expression: 2x² + 8x + 6
Understanding quadratic expressions is a fundamental stepping stone in algebra. This article delves deep into the expression 2x² + 8x + 6, exploring its various facets – from factoring and solving for x to graphing and understanding its real-world applications. We'll unpack this seemingly simple expression, revealing the rich mathematical concepts it embodies. By the end, you'll not only know how to manipulate this specific expression but also gain a broader understanding of quadratic equations and their significance.
Introduction to Quadratic Expressions
A quadratic expression is a polynomial expression of the second degree, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our focus, 2x² + 8x + 6, perfectly fits this mold, with a = 2, b = 8, and c = 6. Understanding quadratic expressions is vital for various mathematical and scientific applications, from calculating projectile trajectories to modeling population growth.
Factoring the Quadratic Expression: Finding the Roots
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions. This process is crucial for solving quadratic equations (when the expression is set equal to zero) and for simplifying more complex expressions. There are several methods to factor quadratic expressions, and we'll explore the most common ones in relation to 2x² + 8x + 6.
1. Greatest Common Factor (GCF): The first step in factoring any polynomial is to look for a greatest common factor among all the terms. In our case, all three terms (2x², 8x, and 6) are divisible by 2. Factoring out the GCF, we get:
2(x² + 4x + 3)
This simplifies the expression, making further factoring easier.
2. Factoring the Trinomial: Now, we need to factor the trinomial within the parentheses: x² + 4x + 3. We look for two numbers that add up to 4 (the coefficient of x) and multiply to 3 (the constant term). These numbers are 1 and 3. Therefore, the factored form of the trinomial is (x + 1)(x + 3).
3. The Complete Factored Form: Combining the GCF and the factored trinomial, we arrive at the completely factored form of our original expression:
2(x + 1)(x + 3)
This factored form is incredibly useful for various purposes, as we will see in the following sections.
Solving the Quadratic Equation: Finding the x-intercepts
A quadratic equation is formed when a quadratic expression is set equal to zero. In our case, the equation is:
2x² + 8x + 6 = 0
Solving this equation means finding the values of 'x' that make the equation true. These values are also known as the roots, zeros, or x-intercepts of the quadratic function. The factored form we derived earlier makes solving this equation much simpler.
Since the product of the three factors is zero, at least one of the factors must be zero. This gives us three possible equations:
- 2 = 0 (This is obviously false)
- x + 1 = 0 => x = -1
- x + 3 = 0 => x = -3
Therefore, the solutions (roots) of the quadratic equation 2x² + 8x + 6 = 0 are x = -1 and x = -3. These are the points where the graph of the quadratic function intersects the x-axis.
Graphical Representation: Visualizing the Parabola
Quadratic functions are graphically represented by parabolas. A parabola is a U-shaped curve that opens either upwards (if 'a' is positive) or downwards (if 'a' is negative). In our case, since a = 2 (positive), the parabola opens upwards.
The x-intercepts we found earlier (-1 and -3) are the points where the parabola crosses the x-axis. The vertex of the parabola, the lowest point, can be found using the formula x = -b / 2a. In our case:
x = -8 / (2 * 2) = -2
Substituting x = -2 back into the original equation gives us the y-coordinate of the vertex:
y = 2(-2)² + 8(-2) + 6 = -2
So, the vertex of the parabola is at the point (-2, -2). The y-intercept (where the parabola crosses the y-axis) is found by setting x = 0:
y = 2(0)² + 8(0) + 6 = 6
Using this information (x-intercepts, vertex, and y-intercept), we can accurately sketch the parabola representing the function y = 2x² + 8x + 6.
The Quadratic Formula: A General Solution
While factoring is a useful method, it doesn't always work for all quadratic equations. The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
Applying this formula to our equation (2x² + 8x + 6 = 0), we get:
x = [-8 ± √(8² - 4 * 2 * 6)] / (2 * 2) x = [-8 ± √(64 - 48)] / 4 x = [-8 ± √16] / 4 x = [-8 ± 4] / 4
This gives us the same solutions as before:
x = (-8 + 4) / 4 = -1 x = (-8 - 4) / 4 = -3
The Discriminant: Understanding the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. The discriminant tells us about the nature of the roots of the quadratic equation:
- If b² - 4ac > 0: The equation has two distinct real roots (as in our case).
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has no real roots; the roots are complex numbers.
In our example, the discriminant is 16 (64 - 48 = 16), which is positive, indicating two distinct real roots.
Real-World Applications of Quadratic Equations
Quadratic equations are not just abstract mathematical concepts; they have numerous practical applications in various fields:
- Physics: Calculating projectile motion (the trajectory of a ball, rocket, etc.), understanding the motion of objects under constant acceleration.
- Engineering: Designing structures, optimizing shapes for strength and efficiency, modeling vibrations and oscillations.
- Economics: Modeling cost functions, revenue functions, and profit maximization.
- Computer Graphics: Creating curves and shapes, modeling lighting and shadows.
- Data Analysis: Finding best-fit curves to data sets.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a quadratic expression and a quadratic equation?
A quadratic expression is a mathematical phrase, like 2x² + 8x + 6. A quadratic equation is formed when a quadratic expression is set equal to zero, such as 2x² + 8x + 6 = 0.
Q2: Can all quadratic equations be factored easily?
No. While some quadratic equations can be factored easily using simple methods, others require more advanced techniques or the quadratic formula for solving.
Q3: What does the vertex of a parabola represent?
The vertex of a parabola represents the minimum (for upward-opening parabolas) or maximum (for downward-opening parabolas) value of the quadratic function. It's also the turning point of the parabola.
Q4: What is the significance of the discriminant?
The discriminant tells us about the nature and number of roots (solutions) of a quadratic equation. It helps determine whether the roots are real or complex, and whether they are distinct or repeated.
Q5: Are there other methods to solve quadratic equations besides factoring and the quadratic formula?
Yes, there are other methods, including completing the square and graphical methods. However, factoring and the quadratic formula are the most widely used techniques.
Conclusion: Mastering Quadratic Expressions
The seemingly simple quadratic expression 2x² + 8x + 6 embodies a wealth of mathematical concepts. By understanding how to factor it, solve the corresponding equation, visualize its graph, and interpret the discriminant, we gain a deeper appreciation of quadratic functions and their widespread applications. This journey through factoring, solving, graphing, and understanding the nuances of the discriminant reinforces the fundamental principles of algebra and lays the groundwork for tackling more complex mathematical problems. Remember, the key to mastering algebra lies in understanding the underlying concepts and applying them consistently. Continue exploring, questioning, and practicing – and you'll be well on your way to becoming proficient in algebra and beyond.
Latest Posts
Latest Posts
-
X3 Cos X 2 1 2
Sep 14, 2025
-
Acoelomate Vs Pseudocoelomate Vs Coelomate
Sep 14, 2025
-
3 Protons And 4 Neutrons
Sep 14, 2025
-
Square Root Of 448 Simplified
Sep 14, 2025
-
What Shapes Have Perpendicular Sides
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2x2 + 8x + 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.