2x 2 3x X 2
thesills
Sep 16, 2025 · 6 min read
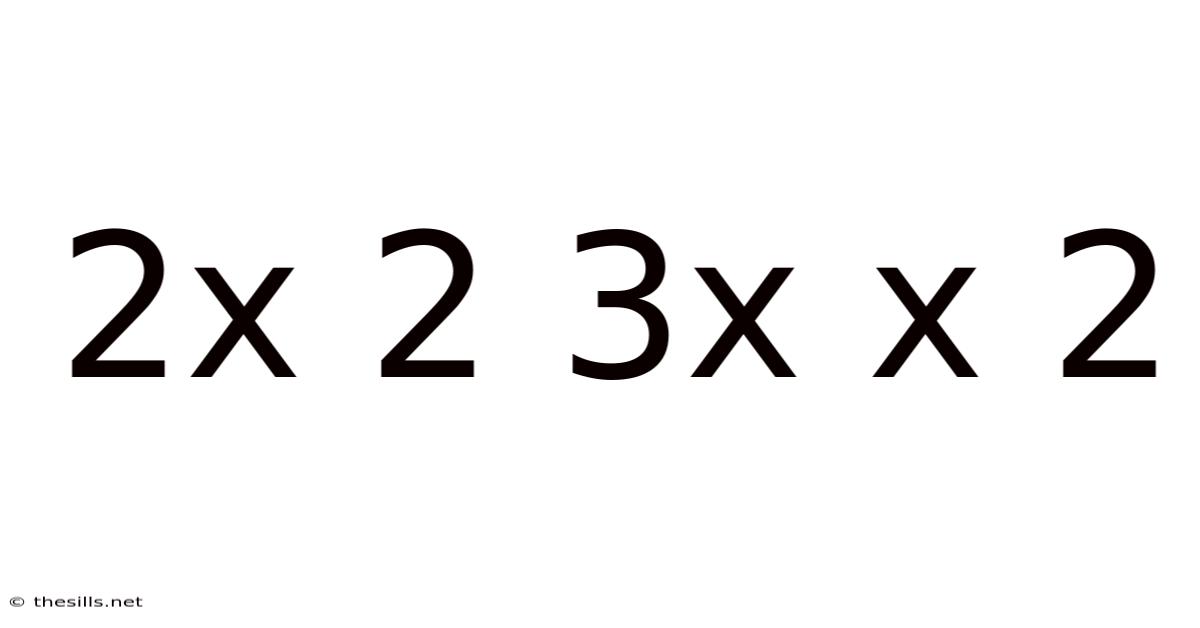
Table of Contents
Decoding the Mathematical Puzzle: 2x² + 3x + 2 = 0
This article delves into the solution and deeper meaning behind the quadratic equation 2x² + 3x + 2 = 0. We will explore various methods for solving this seemingly simple equation, uncovering the underlying mathematical concepts and demonstrating their practical application. Understanding quadratic equations is fundamental to many areas of mathematics, science, and engineering, making this exploration valuable for students and enthusiasts alike. We'll move beyond simply finding the solution and delve into the nature of quadratic equations, their graphical representation, and the significance of the discriminant.
Introduction to Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a is not equal to zero. Our specific equation, 2x² + 3x + 2 = 0, fits this form perfectly, with a = 2, b = 3, and c = 2.
Understanding quadratic equations is crucial because they model numerous real-world phenomena, from the trajectory of a projectile to the shape of a parabola in architecture. The solutions to these equations, often called roots or zeros, represent the points where the corresponding parabola intersects the x-axis.
Method 1: Factoring the Quadratic Expression
Factoring is a powerful technique for solving quadratic equations. It involves expressing the quadratic expression as a product of two simpler expressions. Unfortunately, not all quadratic equations can be easily factored. Let's try factoring 2x² + 3x + 2 = 0:
We look for two numbers that multiply to (a * c) = (2 * 2) = 4 and add up to b = 3. However, there are no such integer pairs. This indicates that this particular quadratic equation doesn't have easily factorable integer solutions. While factoring is a preferred method when possible due to its simplicity, it's not always applicable. Let's move to alternative methods.
Method 2: The Quadratic Formula
The quadratic formula is a powerful tool that provides solutions for any quadratic equation, regardless of whether it's easily factorable. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply the quadratic formula to our equation, 2x² + 3x + 2 = 0:
- a = 2
- b = 3
- c = 2
Substituting these values into the quadratic formula:
x = [-3 ± √(3² - 4 * 2 * 2)] / (2 * 2) x = [-3 ± √(9 - 16)] / 4 x = [-3 ± √(-7)] / 4
Notice that we have a negative number under the square root (√-7). This signifies that the solutions are complex numbers. Complex numbers involve the imaginary unit i, where i² = -1. Therefore, the solutions are:
x = [-3 ± i√7] / 4
This means the equation has two complex roots: x₁ = (-3 + i√7) / 4 and x₂ = (-3 - i√7) / 4. These roots are conjugates of each other, meaning they differ only in the sign of the imaginary part.
Method 3: Completing the Square
Completing the square is another algebraic method for solving quadratic equations. This technique involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's demonstrate this method:
-
Divide by the coefficient of x²: Divide the entire equation by 2: x² + (3/2)x + 1 = 0
-
Move the constant term to the right side: x² + (3/2)x = -1
-
Find the value to complete the square: Take half of the coefficient of x ((3/2)/2 = 3/4), square it ((3/4)² = 9/16), and add it to both sides: x² + (3/2)x + 9/16 = -1 + 9/16 x² + (3/2)x + 9/16 = -7/16
-
Factor the perfect square trinomial: (x + 3/4)² = -7/16
-
Solve for x: x + 3/4 = ±√(-7/16) x = -3/4 ± (i√7)/4
This method yields the same complex roots as the quadratic formula.
The Discriminant: Unveiling the Nature of the Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. The discriminant provides valuable information about the nature of the roots of the quadratic equation:
- If b² - 4ac > 0: The equation has two distinct real roots.
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has two complex conjugate roots.
In our case, for 2x² + 3x + 2 = 0, the discriminant is 3² - 4 * 2 * 2 = 9 - 16 = -7, which is less than 0. This confirms that the equation has two complex conjugate roots, as we found using the other methods.
Graphical Representation
The quadratic equation 2x² + 3x + 2 = 0 represents a parabola. Since the discriminant is negative, the parabola does not intersect the x-axis. This means there are no real solutions (x-intercepts). The parabola opens upwards because the coefficient of x² (a = 2) is positive. The vertex of the parabola represents the minimum point of the curve. The lack of real roots graphically indicates that the parabola lies entirely above the x-axis.
Applications of Quadratic Equations
Quadratic equations have far-reaching applications across various fields:
- Physics: Describing projectile motion, calculating the path of a ball thrown in the air.
- Engineering: Designing parabolic antennas, bridges, and arches.
- Economics: Modeling cost and revenue functions.
- Computer Graphics: Creating curves and shapes.
Frequently Asked Questions (FAQ)
-
Q: Why are complex roots important? A: While they might seem abstract, complex roots are essential in many advanced mathematical concepts and have applications in fields like electrical engineering and signal processing.
-
Q: Can a quadratic equation have only one root? A: Yes, if the discriminant is equal to zero, the equation has a single, repeated real root.
-
Q: How can I check my solutions? A: Substitute the calculated roots back into the original equation. If the equation holds true, the solutions are correct. For complex roots, this requires careful handling of imaginary numbers.
-
Q: What if 'a' is zero? A: If a is zero, the equation is no longer quadratic; it becomes a linear equation.
Conclusion
Solving the quadratic equation 2x² + 3x + 2 = 0 involves understanding different mathematical methods, including factoring (which isn't directly applicable here), the quadratic formula, and completing the square. All three methods consistently reveal the same complex conjugate roots. The significance of the discriminant highlights the nature of these roots, indicating that the parabola represented by this equation lies entirely above the x-axis, having no real-number intersections. The exploration of this seemingly simple equation offers a deep dive into the foundational concepts of quadratic equations, enriching our understanding of their properties and applications in diverse fields. The ability to confidently tackle such equations forms a strong foundation for further mathematical explorations.
Latest Posts
Latest Posts
-
Reaction Of Cac2 With Water
Sep 16, 2025
-
X 2 4x 1 Factored
Sep 16, 2025
-
5 4 As A Percent
Sep 16, 2025
-
Derivative Of Tan 1 2x
Sep 16, 2025
-
Do Transformers Work On Dc
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2x 2 3x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.