X 2 4x 1 Factored
thesills
Sep 16, 2025 · 6 min read
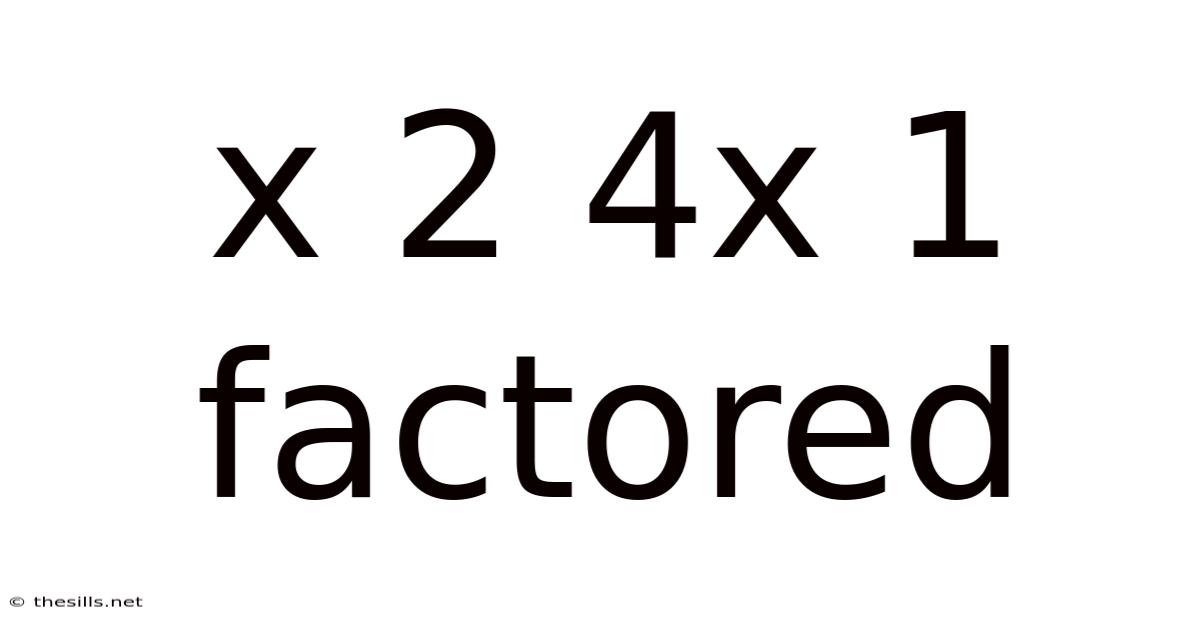
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into x² + 4x + 1
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding many mathematical concepts. This article provides a comprehensive guide to factoring the specific quadratic expression x² + 4x + 1, exploring different methods and delving into the underlying mathematical principles. We'll move beyond simply finding the answer to truly understand why the factoring works, equipping you with the skills to tackle similar problems confidently.
Understanding Quadratic Expressions
Before tackling x² + 4x + 1, let's establish a firm grasp on quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. The expression x² + 4x + 1 fits this mold perfectly, with a = 1, b = 4, and c = 1.
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions (usually linear expressions). This process is the reverse of expanding brackets using the distributive property (often referred to as FOIL – First, Outer, Inner, Last). Successfully factoring a quadratic expression provides valuable insights into its roots (the values of x that make the expression equal to zero), its graph (a parabola), and its behavior.
Method 1: Factoring by Inspection (Trial and Error)
This method involves finding two numbers that add up to the coefficient of the x term (b) and multiply to the constant term (c). For x² + 4x + 1, we're looking for two numbers that add up to 4 and multiply to 1.
Let's try some possibilities:
- 1 and 3? 1 + 3 = 4, but 1 x 3 = 3 (not 1).
- 2 and 2? 2 + 2 = 4, but 2 x 2 = 4 (not 1).
Unfortunately, there are no two integers that satisfy both conditions. This means that x² + 4x + 1 cannot be factored easily using integers. This doesn't mean it's unfactorable; it simply means the factors will involve irrational numbers.
Method 2: Completing the Square
Completing the square is a powerful technique for factoring quadratics and solving quadratic equations. The goal is to manipulate the expression into a perfect square trinomial, which can then be easily factored.
Steps:
- Focus on the x² and x terms: Consider x² + 4x.
- Find half the coefficient of the x term: Half of 4 is 2.
- Square the result: 2² = 4.
- Add and subtract the result within the expression: This maintains the original value. x² + 4x + 4 - 4 + 1.
- Rewrite as a perfect square trinomial: (x² + 4x + 4) - 3 = (x + 2)² - 3.
Therefore, the factored form using completing the square is (x + 2)² - 3. This is a difference of squares, but it's not factored completely into two linear binomials with integer coefficients.
Method 3: Quadratic Formula
The quadratic formula is a universal method for finding the roots (or zeros) of any quadratic equation of the form ax² + bx + c = 0. The roots are given by:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 4x + 1 = 0, a = 1, b = 4, and c = 1. Plugging these values into the quadratic formula, we get:
x = [-4 ± √(4² - 4 * 1 * 1)] / (2 * 1) x = [-4 ± √(16 - 4)] / 2 x = [-4 ± √12] / 2 x = [-4 ± 2√3] / 2 x = -2 ± √3
The roots are x = -2 + √3 and x = -2 - √3.
These roots can be used to factor the quadratic expression. Since the roots are α = -2 + √3 and β = -2 - √3, the factored form is:
(x - α)(x - β) = (x - (-2 + √3))(x - (-2 - √3)) = (x + 2 - √3)(x + 2 + √3)
This demonstrates that while the original expression doesn't factor neatly with integers, it does have real roots and can be factored using the roots derived from the quadratic formula.
The Discriminant and the Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. It determines the nature of the roots:
- b² - 4ac > 0: Two distinct real roots.
- b² - 4ac = 0: One real root (a repeated root).
- b² - 4ac < 0: Two complex conjugate roots (involving imaginary numbers).
In our case, b² - 4ac = 16 - 4 = 12 > 0, indicating two distinct real roots, as we found using the quadratic formula.
Graphical Representation
The graph of y = x² + 4x + 1 is a parabola. The roots we calculated (-2 + √3 and -2 - √3) represent the x-intercepts (where the parabola crosses the x-axis). The vertex of the parabola (the minimum point) can be found using the formula x = -b/2a = -4/2 = -2. Substituting this into the original equation gives y = (-2)² + 4(-2) + 1 = -3. Therefore, the vertex is at (-2, -3).
Understanding the graph helps visualize the behavior of the quadratic expression and its roots. The fact that the parabola intersects the x-axis at two points confirms the existence of two real roots.
Applications of Factoring Quadratic Expressions
Factoring quadratic expressions is not just an abstract algebraic exercise; it has numerous practical applications in various fields:
- Physics: Solving projectile motion problems, where the trajectory is often modeled by a quadratic equation.
- Engineering: Designing structures, analyzing circuits, and optimizing systems.
- Economics: Modeling economic growth, supply and demand curves, and cost functions.
- Computer science: Developing algorithms and solving optimization problems.
Mastering factoring techniques provides a crucial foundation for tackling more complex problems in these areas.
Frequently Asked Questions (FAQ)
Q: Why can't x² + 4x + 1 be factored easily using integers?
A: Because there are no two integers that add up to 4 and multiply to 1 simultaneously. The roots of the quadratic equation are irrational numbers, which leads to factors involving radicals (square roots).
Q: Is completing the square always the best method for factoring?
A: Not necessarily. Completing the square is a powerful general method, but factoring by inspection (when possible) is often quicker and simpler. The quadratic formula always works but might involve more computation. The best method depends on the specific quadratic expression and your preference.
Q: What does it mean if the discriminant is negative?
A: A negative discriminant means that the quadratic equation has no real roots. The roots are complex numbers involving the imaginary unit i (√-1). The parabola representing the quadratic function does not intersect the x-axis.
Q: Can all quadratic expressions be factored?
A: Yes, all quadratic expressions can be factored, either into linear expressions with real or complex coefficients. However, factoring with integer coefficients is not always possible.
Conclusion
Factoring the quadratic expression x² + 4x + 1 demonstrates that while simple integer factoring might not always be possible, alternative methods like completing the square and the quadratic formula provide powerful tools for finding the factors and gaining a deeper understanding of the expression's behavior. The discriminant helps determine the nature of the roots, and the graphical representation provides a visual interpretation of the solution. Mastering these techniques is crucial for success in algebra and its numerous applications in other scientific and engineering disciplines. Remember, the key is not just to find the answer but to understand the underlying mathematical principles and apply the most appropriate method for each problem. The more you practice, the more confident and efficient you will become in factoring quadratic expressions and solving related problems.
Latest Posts
Latest Posts
-
Slip On A Banana Peel
Sep 16, 2025
-
What Is A Vinyl Halide
Sep 16, 2025
-
Lines Of Symmetry In Square
Sep 16, 2025
-
Formula Of Carbon And Oxygen
Sep 16, 2025
-
Is Fe Paramagnetic Or Diamagnetic
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 4x 1 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.