12 25 As A Decimal
thesills
Sep 16, 2025 · 5 min read
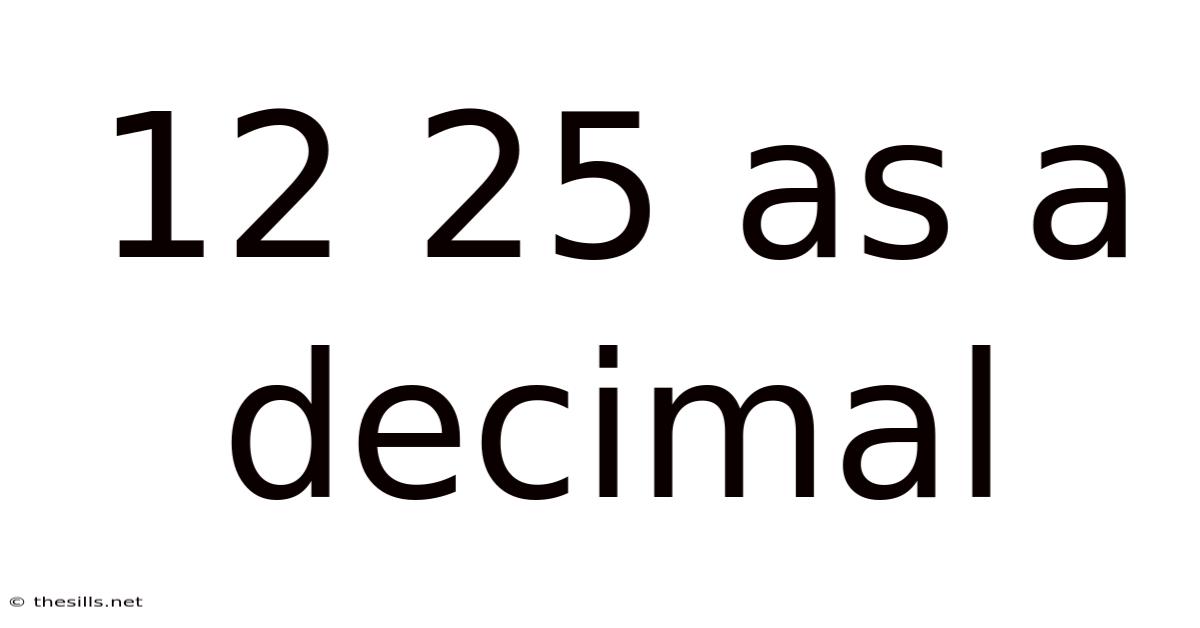
Table of Contents
Decoding 12/25 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will delve into the conversion of the fraction 12/25 into its decimal form, exploring various methods and providing a detailed explanation suitable for learners of all levels. We'll cover the basic process, explore alternative approaches, and address common questions, solidifying your understanding of this core mathematical concept.
Introduction: Why Convert Fractions to Decimals?
Fractions and decimals represent the same concept: parts of a whole. While fractions use a numerator and a denominator (e.g., 12/25), decimals express these parts using a base-ten system (e.g., 0.48). Converting between fractions and decimals is crucial for various reasons:
- Calculations: Decimals often simplify calculations, particularly when using calculators or computers.
- Comparisons: Comparing fractions can be challenging, but comparing decimals is straightforward.
- Real-world applications: Many real-world measurements and values are expressed as decimals (e.g., money, weight, length).
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. In the case of 12/25, we simply divide the numerator (12) by the denominator (25):
12 ÷ 25 = 0.48
Therefore, 12/25 as a decimal is 0.48. This method is simple and can be performed using a calculator or by hand using long division. Let's break down the long division process for those who prefer a manual approach:
Long Division: A Step-by-Step Guide
-
Set up the division: Write 12 as the dividend (inside the division bracket) and 25 as the divisor (outside the bracket). Since 25 is larger than 12, we add a decimal point after 12 and add a zero: 12.0.
-
Divide: How many times does 25 go into 120? It goes in 4 times (4 x 25 = 100). Write 4 above the zero in the dividend.
-
Subtract: Subtract 100 from 120, leaving a remainder of 20.
-
Bring down: Bring down another zero from the dividend, making it 200.
-
Divide again: How many times does 25 go into 200? It goes in 8 times (8 x 25 = 200). Write 8 above the newly brought down zero.
-
Subtract again: Subtract 200 from 200, leaving a remainder of 0. Since the remainder is 0, we have reached the end of the division.
The result is 0.48.
Method 2: Finding an Equivalent Fraction with a Denominator of 10, 100, or 1000
An alternative approach involves manipulating the fraction to have a denominator that is a power of 10 (10, 100, 1000, etc.). This directly converts the fraction into a decimal. While not always possible, it's a useful technique when applicable.
In this case, we can convert 25 to 100 by multiplying by 4: 25 x 4 = 100. To maintain the fraction's value, we must also multiply the numerator by 4: 12 x 4 = 48. This gives us the equivalent fraction:
48/100
Since 100 is 10², this fraction easily translates to a decimal: 0.48.
Method 3: Using a Calculator
The simplest method, especially for complex fractions, is to use a calculator. Simply enter 12 ÷ 25 and the calculator will provide the decimal equivalent: 0.48. This method is efficient and avoids the potential for errors during manual calculations.
Understanding the Decimal Value: 0.48
The decimal 0.48 represents 48 hundredths or 48/100. This means it's slightly less than half (0.5 or 50/100). Understanding the place value is key:
- 0: Represents the whole number part (zero in this case).
- 4: Represents the tenths place (four-tenths).
- 8: Represents the hundredths place (eight-hundredths).
Therefore, 0.48 signifies 48 parts out of 100 equal parts of a whole.
Applications of 12/25 and 0.48
The fraction 12/25 and its decimal equivalent, 0.48, have various practical applications. For example:
- Percentage: 0.48 is equivalent to 48%. This can be used to calculate discounts, sales tax, or percentages in various contexts.
- Measurements: If you have a measurement system using 25 units as a whole, 12/25 or 0.48 represents 12 of those units. This can apply to inches, centimeters, or any other unit of measurement.
- Proportions: The fraction and its decimal equivalent can be used to solve proportion problems, where a part of a whole is known and the value of the whole needs to be determined.
Frequently Asked Questions (FAQs)
-
Q: Can all fractions be converted to terminating decimals?
- A: No. Fractions with denominators that have prime factors other than 2 and 5 will result in non-terminating, repeating decimals.
-
Q: What is the difference between a terminating and a repeating decimal?
- A: A terminating decimal has a finite number of digits after the decimal point (e.g., 0.48). A repeating decimal has a pattern of digits that repeats indefinitely (e.g., 1/3 = 0.333...).
-
Q: How do I convert a repeating decimal back to a fraction?
- A: This process involves algebra and assigning a variable to the repeating decimal. Then, you manipulate the equation to isolate the repeating part and express it as a fraction.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions to decimals is a fundamental mathematical skill with numerous real-world applications. The conversion of 12/25 to 0.48, as demonstrated through various methods, highlights the ease and importance of this conversion. Understanding the underlying principles and different approaches allows for flexibility and efficiency when dealing with fractions and decimals in various mathematical and real-world scenarios. Whether using long division, equivalent fractions, or a calculator, the key takeaway is the consistent outcome: 12/25 is accurately represented as the decimal 0.48. By mastering this fundamental concept, you build a strong foundation for more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
How To Find Population Growth
Sep 16, 2025
-
What Is 9 X 5
Sep 16, 2025
-
What Is 12 Of 40000
Sep 16, 2025
-
H2o Co2 H2co3 H Hco3
Sep 16, 2025
-
Young Horse Is Called What
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 12 25 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.