1 1 X 2 Derivative
thesills
Sep 12, 2025 · 6 min read
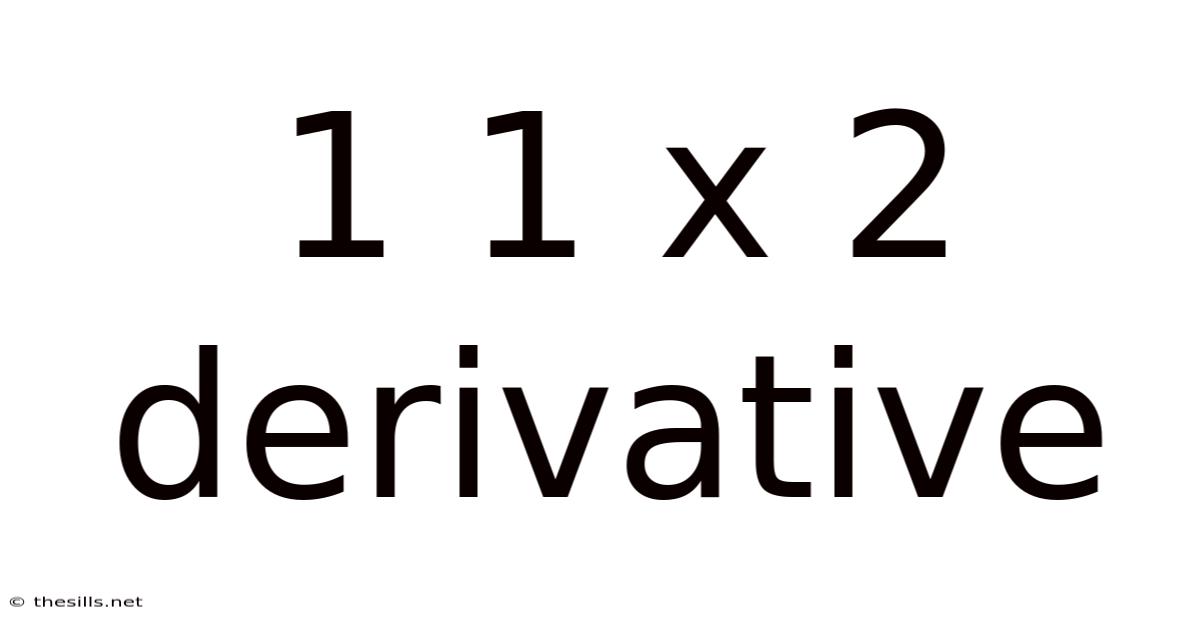
Table of Contents
Understanding the Derivative of 1/(1+x)²: A Comprehensive Guide
The derivative of 1/(1+x)² is a fundamental concept in calculus with applications spanning various fields, from physics and engineering to economics and finance. This comprehensive guide will walk you through understanding this derivative, not just by providing the answer, but by exploring the underlying principles and techniques involved. We'll cover different approaches to finding the derivative, explain the underlying mathematical concepts, and address frequently asked questions. This will equip you with a solid grasp of this crucial derivative and its implications.
1. Introduction: Why is this Derivative Important?
The function f(x) = 1/(1+x)² represents a rational function, a type of function expressed as the ratio of two polynomials. Understanding its derivative is crucial for several reasons:
- Optimization Problems: Derivatives are essential in finding maxima and minima of functions, crucial in optimization problems across various disciplines. Knowing the derivative of 1/(1+x)² allows us to analyze its behavior and find critical points.
- Rate of Change: The derivative represents the instantaneous rate of change of a function. In the context of 1/(1+x)², the derivative tells us how rapidly the function's value changes at any given point.
- Taylor and Maclaurin Series: This derivative is often encountered when working with Taylor and Maclaurin series expansions, powerful tools for approximating functions.
- Differential Equations: The function and its derivative might appear in differential equations, which are used to model dynamic systems in numerous fields.
Understanding its derivative, therefore, unlocks a gateway to solving problems and gaining deeper insights into many mathematical and scientific applications.
2. Finding the Derivative using the Quotient Rule
One of the most straightforward ways to find the derivative of 1/(1+x)² is by applying the quotient rule. The quotient rule states that the derivative of a function f(x) = g(x)/h(x) is given by:
f'(x) = [h(x)g'(x) - g(x)h'(x)] / [h(x)]²
In our case, g(x) = 1 and h(x) = (1+x)². Therefore:
- g'(x) = 0 (the derivative of a constant is zero)
- h'(x) = 2(1+x) (using the chain rule: d/dx (1+x)² = 2(1+x) * d/dx (1+x) = 2(1+x))
Substituting these values into the quotient rule formula, we get:
f'(x) = [(1+x)² * 0 - 1 * 2(1+x)] / [(1+x)²]²
Simplifying this expression, we obtain:
f'(x) = -2(1+x) / (1+x)^4
Further simplification by canceling out one (1+x) term from the numerator and denominator results in:
f'(x) = -2 / (1+x)³
This is the derivative of 1/(1+x)².
3. Finding the Derivative using the Chain Rule and Power Rule
Alternatively, we can rewrite the function as (1+x)^(-2) and then apply the chain rule and power rule. The power rule states that the derivative of xⁿ is nxⁿ⁻¹. The chain rule states that the derivative of a composite function f(g(x)) is f'(g(x)) * g'(x).
Applying these rules:
- Rewrite the function: f(x) = (1+x)^(-2)
- Apply the power rule: The derivative of x⁻² is -2x⁻³.
- Apply the chain rule: We need to multiply by the derivative of the inner function (1+x), which is 1.
Therefore:
f'(x) = -2(1+x)^(-3) * 1
Simplifying this gives us the same result as before:
f'(x) = -2 / (1+x)³
4. Graphical Interpretation of the Derivative
The derivative, -2/(1+x)³, represents the slope of the tangent line to the curve y = 1/(1+x)² at any given point x. Let's analyze the behavior of this derivative:
- Sign of the Derivative: The derivative is always negative for x > -1. This means the function 1/(1+x)² is always decreasing for x > -1.
- Asymptotic Behavior: As x approaches -1 from the right (x → -1⁺), the derivative approaches negative infinity. This indicates a vertical asymptote at x = -1, where the slope of the tangent becomes infinitely steep. As x approaches infinity (x → ∞), the derivative approaches 0, meaning the function flattens out.
Understanding the graphical behavior allows us to visualize how the rate of change of the function varies across its domain.
5. Applications in Different Fields
The derivative of 1/(1+x)² finds applications in various fields:
- Physics: In mechanics, this derivative might appear in equations describing the motion of particles under certain forces.
- Engineering: It can be used in analyzing the behavior of electrical circuits or mechanical systems.
- Economics: In modeling economic growth or decay, similar functions and their derivatives are used.
- Probability and Statistics: Functions of this form appear in probability density functions, and their derivatives are crucial for statistical analysis.
The broad applicability underscores the importance of mastering the calculation and interpretation of this derivative.
6. Further Exploration: Higher-Order Derivatives
We can also calculate higher-order derivatives of 1/(1+x)². The second derivative, for instance, is found by differentiating the first derivative:
f'(x) = -2(1+x)⁻³
f''(x) = d/dx [-2(1+x)⁻³] = 6(1+x)⁻⁴ = 6/(1+x)⁴
Higher-order derivatives are valuable tools in advanced mathematical analysis and applications such as Taylor series expansions.
7. Frequently Asked Questions (FAQ)
Q1: What happens when x = -1?
A1: At x = -1, the function 1/(1+x)² and its derivative are undefined. This is because there is a vertical asymptote at x = -1. The function approaches infinity as x approaches -1.
Q2: Can this derivative be found using other methods?
A2: Yes, other techniques such as logarithmic differentiation can also be used. Logarithmic differentiation involves taking the natural logarithm of both sides of the equation before differentiating.
Q3: What is the significance of the negative sign in the derivative?
A3: The negative sign indicates that the function 1/(1+x)² is decreasing for x > -1. The slope of the tangent line is always negative in this region.
8. Conclusion: Mastering a Fundamental Concept
The derivative of 1/(1+x)², which is -2/(1+x)³, is a fundamental result in calculus with wide-ranging applications. By understanding the different methods for finding this derivative—the quotient rule and the chain rule with the power rule—and grasping its graphical interpretation, you've significantly expanded your understanding of calculus. This knowledge serves as a stepping stone to tackling more complex problems and delving deeper into the many fields where this derivative plays a crucial role. Remember, practicing and applying these concepts is key to mastering calculus and its numerous applications. The journey of learning calculus is a continuous process of exploration and discovery, and every mastered concept brings you closer to a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
2 X 2 X 1
Sep 12, 2025
-
Levels Of Organization Of Animals
Sep 12, 2025
-
Positive Result For Biuret Test
Sep 12, 2025
-
How To Find Equivalent Decimals
Sep 12, 2025
-
Is Bacteria Autotrophic Or Heterotrophic
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 1 X 2 Derivative . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.