2 X 2 X 1
thesills
Sep 12, 2025 · 6 min read
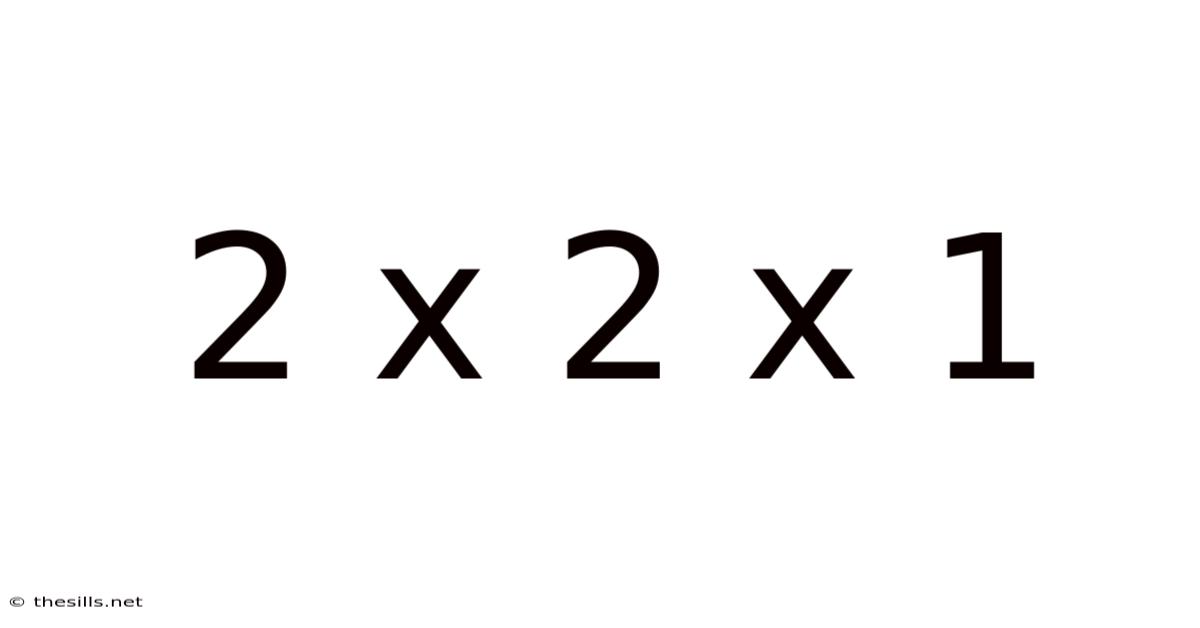
Table of Contents
Exploring the Mathematical and Spatial Dimensions of 2 x 2 x 1: A Deep Dive
This article delves into the multifaceted interpretations and applications of the seemingly simple expression "2 x 2 x 1." We'll move beyond its basic arithmetic calculation to explore its implications in various fields, including mathematics, geometry, spatial reasoning, and even real-world applications. This exploration will offer a comprehensive understanding of this numerical expression, going beyond the simple answer and unveiling its hidden complexities and potential. Understanding 2 x 2 x 1 is not just about multiplication; it's about understanding dimensions, volume, and the power of simple mathematical constructs.
The Basics: Arithmetic Calculation
At its most fundamental level, 2 x 2 x 1 is a straightforward multiplication problem. Following the order of operations, we calculate:
2 x 2 = 4 4 x 1 = 4
Therefore, the arithmetic result of 2 x 2 x 1 is 4. This simple calculation forms the bedrock of our further exploration, acting as the foundation upon which we build a more nuanced understanding.
Geometrical Representation: Volume and Dimensions
The expression "2 x 2 x 1" immediately evokes a three-dimensional representation. We can visualize this as a rectangular prism (or cuboid) with dimensions of 2 units in length, 2 units in width, and 1 unit in height. This geometrical interpretation opens up several avenues of exploration:
-
Volume: The numerical result of 4 corresponds to the volume of this rectangular prism. The volume is calculated as length x width x height, which in this case is 2 x 2 x 1 = 4 cubic units. Understanding this connection between arithmetic and geometry is crucial for grasping the broader implications of the expression.
-
Surface Area: We can also calculate the surface area of this prism. The surface area is the sum of the areas of all six faces. In this case, there are two faces with area 2 x 2 (4 square units each), two faces with area 2 x 1 (2 square units each), and two faces with area 2 x 1 (2 square units each). This gives us a total surface area of 4 + 4 + 2 + 2 + 2 + 2 = 16 square units. This shows that even a seemingly simple shape holds complex mathematical relationships.
-
Spatial Reasoning: Visualizing this 2 x 2 x 1 prism enhances our spatial reasoning skills. We can mentally rotate the prism, consider its projections onto different planes, and understand its orientation in three-dimensional space. This exercise is beneficial for developing problem-solving abilities in fields ranging from architecture to engineering.
Beyond the Rectangular Prism: Exploring Variations
While a 2 x 2 x 1 rectangular prism is the most intuitive geometrical representation, the expression can also be interpreted in other ways:
-
Arrangement of Objects: Imagine arranging objects in a grid. You could arrange four objects in a 2 x 2 square, representing the 2 x 2 part, and then consider a single layer or height of 1. This provides a practical application of the concept in diverse scenarios, such as arranging furniture, organizing storage, or even planning a garden.
-
Data Representation: In data analysis or computer science, the expression could represent a data structure with 2 rows, 2 columns, and 1 layer (or depth). This type of structure is common in matrices or arrays. The numerical value of 4 would then represent the total number of data points in the structure.
Real-world Applications
The seemingly simple expression 2 x 2 x 1 finds surprising applications in many real-world scenarios:
-
Construction and Engineering: The calculation of volume is critical in construction. A contractor might use these calculations to determine the amount of concrete needed for a small foundation, the volume of a storage unit, or the capacity of a simple container.
-
Packaging and Logistics: The 2 x 2 x 1 dimensions could represent the dimensions of a small package. Understanding the volume and surface area is important for optimizing packaging design and minimizing shipping costs.
-
Everyday Life: Consider arranging items on a shelf, stacking books, or even organizing items in a drawer. The intuitive application of understanding dimensions and volume helps in efficient space management.
Expanding the Concept: Variations and Generalizations
Let’s explore what happens when we generalize the expression:
-
Changing the Numbers: What if we change the dimensions to 3 x 3 x 1, or 2 x 3 x 2? This leads to a broader understanding of volume calculations and spatial reasoning in three dimensions. Each variation presents a different shape and volume, reinforcing the connection between the numerical expression and its geometrical interpretation.
-
Higher Dimensions: While 2 x 2 x 1 represents a three-dimensional object, the concept can be extended to higher dimensions. Imagine a four-dimensional hypercube, where the expression might represent a slice or sub-section of that hypercube. This concept is crucial in advanced mathematical fields and theoretical physics.
Mathematical Explorations: Number Theory and Algebra
Beyond geometry, the expression "2 x 2 x 1" can be explored through a mathematical lens:
-
Factorization: The number 4 (the result of 2 x 2 x 1) has several factors: 1, 2, and 4. This leads to explorations of prime factorization and other number theory concepts.
-
Algebraic Expressions: The expression can be generalized as a x b x c, where a, b, and c represent variables. Manipulating this algebraic expression allows for solving equations and exploring relationships between variables. This introduces a level of abstraction that extends the understanding beyond simple numerical calculations.
FAQs (Frequently Asked Questions)
-
What is the most common geometrical shape represented by 2 x 2 x 1? The most common shape is a rectangular prism (or cuboid).
-
Can 2 x 2 x 1 represent other shapes besides a rectangular prism? While a rectangular prism is the most direct representation, it could, with creative interpretation, represent other shapes if the units are not considered to be orthogonal.
-
What is the significance of the order of the numbers in 2 x 2 x 1? In multiplication, the order doesn't affect the final result (commutative property). However, the order significantly changes the geometrical interpretation of the dimensions (length, width, height).
Conclusion: A Deeper Appreciation
The simple expression "2 x 2 x 1" offers a surprisingly rich exploration across various domains. It serves as a gateway to understanding fundamental mathematical principles, spatial reasoning, and their real-world applications. From basic arithmetic to complex geometrical interpretations and algebraic generalizations, this seemingly simple numerical expression reveals depths far beyond its initial appearance. By exploring its facets, we develop a stronger mathematical intuition, enhanced spatial reasoning capabilities, and a greater appreciation for the interconnectedness of mathematical concepts. The journey from a simple calculation to a multifaceted understanding highlights the power of mathematical exploration and the beauty of seemingly simple mathematical constructs. It encourages a deeper appreciation for the elegance and power hidden within seemingly basic mathematical concepts.
Latest Posts
Latest Posts
-
Lewis Dot Symbol Of Mg
Sep 12, 2025
-
In The Ellipse Shown Below
Sep 12, 2025
-
Moment Of Inertia For Hoop
Sep 12, 2025
-
Why Electronic Energy Is Negative
Sep 12, 2025
-
Calcium Sulfate Dihydrate Chemical Formula
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.