X2 + 6x + 9
thesills
Sep 17, 2025 · 6 min read
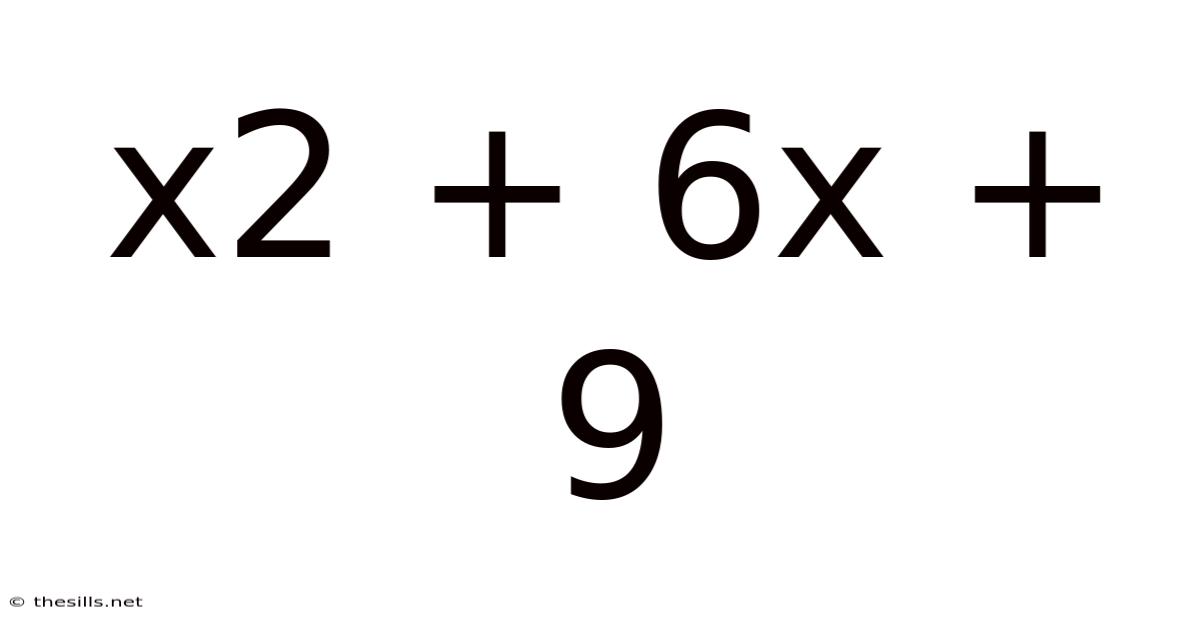
Table of Contents
Unraveling the Mystery of x² + 6x + 9: A Deep Dive into Quadratic Expressions
This article explores the quadratic expression x² + 6x + 9, delving into its various aspects, from its basic factorization and graphical representation to its applications in real-world scenarios. We'll examine its properties, solve related equations, and uncover the underlying mathematical concepts. This comprehensive guide is designed for students and anyone interested in deepening their understanding of algebra. Understanding this seemingly simple expression unlocks a gateway to a wider comprehension of quadratic equations and their significance in mathematics.
Introduction: Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants, and a is not equal to zero. Our focus, x² + 6x + 9, fits neatly into this framework, with a = 1, b = 6, and c = 9. This specific expression holds particular interest because it's a perfect square trinomial, a concept we'll explore in detail.
Factoring the Expression: Unveiling the Perfect Square Trinomial
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions. For x² + 6x + 9, factoring reveals a significant characteristic: it's a perfect square trinomial. This means it can be expressed as the square of a binomial. Let's see how:
We look for two numbers that add up to 6 (the coefficient of x) and multiply to 9 (the constant term). These numbers are 3 and 3. Therefore, we can factor x² + 6x + 9 as follows:
x² + 6x + 9 = (x + 3)(x + 3) = (x + 3)²
This factorization demonstrates that x² + 6x + 9 is the square of the binomial (x + 3). This property is crucial for solving equations and simplifying more complex algebraic expressions.
Graphical Representation: Visualizing the Parabola
Quadratic expressions are graphically represented by parabolas. Parabolas are U-shaped curves that open either upwards or downwards, depending on the sign of the coefficient of the x² term. In our case, since the coefficient of x² is positive (1), the parabola opens upwards.
The vertex of the parabola, the lowest point in this case, represents the minimum value of the quadratic expression. For a perfect square trinomial like x² + 6x + 9, finding the vertex is straightforward. The x-coordinate of the vertex is given by -b/2a = -6/(2*1) = -3. Substituting x = -3 into the expression gives the y-coordinate: (-3)² + 6(-3) + 9 = 0. Therefore, the vertex of the parabola is at the point (-3, 0).
The parabola intersects the x-axis (where y = 0) at the roots of the quadratic equation x² + 6x + 9 = 0. Since the expression is a perfect square, it has a repeated root at x = -3. This means the parabola touches the x-axis at only one point, its vertex.
The y-intercept (where x = 0) is simply the constant term, which is 9. This means the parabola passes through the point (0, 9).
Solving the Quadratic Equation: Finding the Roots
The quadratic equation associated with our expression is x² + 6x + 9 = 0. Since we've already factored the expression as (x + 3)², solving the equation becomes quite simple:
(x + 3)² = 0
Taking the square root of both sides:
x + 3 = 0
Therefore, x = -3. This indicates that the equation has a single, repeated real root at x = -3. This aligns perfectly with our graphical representation, where the parabola touches the x-axis only at x = -3.
Alternative Methods for Solving the Quadratic Equation
While factoring is the most straightforward method for this specific perfect square trinomial, let's briefly explore other methods applicable to solving quadratic equations in general:
- Quadratic Formula: The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
Applying this to our equation (a = 1, b = 6, c = 9):
x = [-6 ± √(6² - 4 * 1 * 9)] / 2 * 1 = [-6 ± √0] / 2 = -3
This confirms our previous result.
- Completing the Square: This method involves manipulating the equation to create a perfect square trinomial on one side. While less efficient for this particular example, it's a valuable technique for solving other quadratic equations.
Applications in Real-World Scenarios
Quadratic equations and expressions, like x² + 6x + 9, have numerous applications in various fields:
-
Physics: Projectile motion, where the trajectory of an object under gravity is described by a quadratic equation. Understanding the vertex of the parabola can help determine the maximum height reached by a projectile.
-
Engineering: Designing parabolic antennas and reflectors, where the shape is crucial for focusing signals.
-
Economics: Modeling profit, cost, and revenue functions, where quadratic equations can help determine optimal production levels.
-
Computer Graphics: Creating curves and shapes in computer-aided design (CAD) software.
Expanding Understanding: Exploring Related Concepts
Understanding x² + 6x + 9 opens doors to several related mathematical concepts:
-
Discriminant: The discriminant (b² - 4ac) in the quadratic formula determines the nature of the roots. A discriminant of zero, as in our case, indicates a single, repeated real root. A positive discriminant signifies two distinct real roots, while a negative discriminant means two complex roots.
-
Vertex Form: Quadratic expressions can be written in vertex form: a(x - h)² + k, where (h, k) represents the vertex. Our expression, in vertex form, is 1(x - (-3))² + 0, clearly showing the vertex at (-3, 0).
-
Polynomial Division: While not directly applicable here, polynomial division is a powerful tool for simplifying or factoring more complex polynomial expressions.
Frequently Asked Questions (FAQ)
- Q: What makes x² + 6x + 9 a special case?
A: It's a perfect square trinomial, meaning it factors into the square of a binomial (x + 3)². This simplifies its analysis and solution significantly.
- Q: Can this expression ever be negative?
A: No. Since it's a perfect square, (x+3)², it will always be greater than or equal to zero. The minimum value is 0, achieved at x = -3.
- Q: How is this expression used in calculus?
A: In calculus, the derivative of this expression is 2x + 6, which helps in finding critical points (like the minimum point, which is the vertex). The second derivative is 2, indicating the parabola is concave upwards.
- Q: Are there other perfect square trinomials?
A: Yes, many. For example, x² + 8x + 16 = (x + 4)² and x² - 10x + 25 = (x - 5)². The general form is a² + 2ab + b² = (a + b)².
Conclusion: The Significance of x² + 6x + 9
The seemingly simple expression x² + 6x + 9 provides a solid foundation for understanding more complex algebraic concepts. Its perfect square trinomial nature simplifies factoring and solving equations, leading to a better grasp of quadratic functions, graphical representations (parabolas), and real-world applications. Mastering this foundational expression is key to unlocking further advancements in algebra and its related fields. This exploration has hopefully not only answered questions about the expression itself but has also sparked a deeper curiosity about the broader world of quadratic equations and their uses in various disciplines. The journey into understanding mathematics is a continuous process of building upon fundamental concepts, and this expression serves as a perfect stepping stone in that journey.
Latest Posts
Latest Posts
-
Uncatalyzed Vs Catalyzed Reaction Graph
Sep 17, 2025
-
66 2 3 As A Fraction
Sep 17, 2025
-
Is Graphite A Pure Substance
Sep 17, 2025
-
Vapor Pressure Of N Heptane
Sep 17, 2025
-
If The Temperature Is Increased
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about X2 + 6x + 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.