X2 3x 10 0 Solution
thesills
Sep 12, 2025 · 5 min read
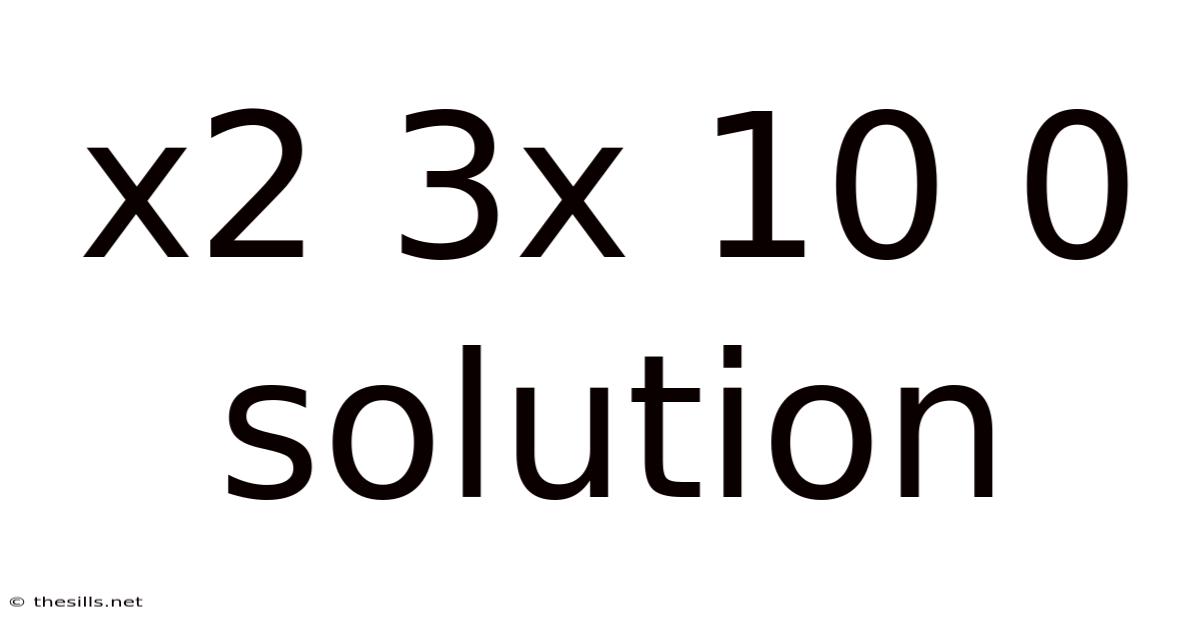
Table of Contents
Solving the Quadratic Equation: x² + 3x + 10 = 0
This article explores the solution to the quadratic equation x² + 3x + 10 = 0. We'll delve into various methods for solving quadratic equations, focusing on this specific example and highlighting the significance of understanding complex numbers in mathematics. Understanding quadratic equations is crucial in many fields, from physics and engineering to finance and computer science. This seemingly simple equation opens the door to a deeper understanding of mathematical concepts.
Introduction to Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Solving a quadratic equation means finding the values of x that satisfy the equation – the values that make the equation true. There are several methods to solve these equations, including factoring, using the quadratic formula, and completing the square.
Attempting to Solve x² + 3x + 10 = 0 by Factoring
The simplest method is factoring. We look for two numbers that add up to 'b' (the coefficient of x, which is 3 in this case) and multiply to 'c' (the constant term, which is 10). However, there are no two real numbers that satisfy this condition. The pairs (1, 10), (2, 5), (-1, -10), and (-2, -5) all fail to add up to 3. This indicates that the solution to this quadratic equation involves numbers beyond the realm of real numbers.
Understanding the Quadratic Formula
When factoring doesn't work, the quadratic formula provides a guaranteed solution for any quadratic equation. The quadratic formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
In our equation, x² + 3x + 10 = 0, a = 1, b = 3, and c = 10. Let's substitute these values into the quadratic formula:
x = [-3 ± √(3² - 4 * 1 * 10)] / (2 * 1)
x = [-3 ± √(9 - 40)] / 2
x = [-3 ± √(-31)] / 2
Introducing Complex Numbers
Here's where we encounter an important concept: the square root of a negative number. The square root of -31 is not a real number. Real numbers are numbers that can be plotted on a number line. To address this, we introduce complex numbers.
A complex number is a number that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit, defined as the square root of -1 (i² = -1).
In our case, √(-31) can be expressed as √(31) * √(-1) = √31i. Therefore, the solutions to our quadratic equation are:
x = [-3 + √31i] / 2 and x = [-3 - √31i] / 2
These are complex conjugate pairs. Complex conjugate pairs always appear when solving quadratic equations with real coefficients that have no real solutions.
Graphical Representation of Complex Solutions
While real number solutions can be represented on a number line, complex number solutions require a two-dimensional plane called the complex plane or Argand plane. The horizontal axis represents the real part (a) of the complex number, and the vertical axis represents the imaginary part (b). Our solutions, [-3 + √31i] / 2 and [-3 - √31i] / 2, can be plotted as points on this plane.
The Discriminant and Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. The discriminant determines the nature of the roots (solutions) of a quadratic equation:
- If b² - 4ac > 0: The equation has two distinct real roots.
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has two complex conjugate roots (which are not real).
In our equation, x² + 3x + 10 = 0, the discriminant is 9 - 40 = -31, which is less than 0. This confirms that the equation has two complex conjugate roots, as we've already found.
Completing the Square Method for x² + 3x + 10 = 0
Another method for solving quadratic equations is completing the square. This involves manipulating the equation to create a perfect square trinomial. Let's apply this method to our equation:
x² + 3x + 10 = 0
First, move the constant term to the right side:
x² + 3x = -10
Next, take half of the coefficient of x (which is 3/2), square it (9/4), and add it to both sides:
x² + 3x + 9/4 = -10 + 9/4
Now, the left side is a perfect square trinomial:
(x + 3/2)² = -31/4
Take the square root of both sides:
x + 3/2 = ±√(-31/4) = ±(√31/2)i
Finally, solve for x:
x = -3/2 ± (√31/2)i
This result is identical to the solution obtained using the quadratic formula, demonstrating the equivalence of the methods.
Applications of Complex Numbers
Although they might seem abstract, complex numbers have many practical applications in various fields:
- Electrical Engineering: Complex numbers are used extensively in analyzing alternating current (AC) circuits, representing impedance and phase relationships.
- Quantum Mechanics: Complex numbers are fundamental to the mathematical framework of quantum mechanics, describing wave functions and probabilities.
- Signal Processing: Complex numbers are used in Fourier analysis, which is crucial for processing and analyzing signals in many applications.
- Fluid Dynamics: Complex analysis helps solve certain types of fluid flow problems.
Frequently Asked Questions (FAQ)
Q1: Why are complex numbers necessary to solve this equation?
A1: Because the discriminant is negative, indicating that there are no real number solutions. Complex numbers extend the number system to encompass solutions to equations that have no real counterparts.
Q2: Can all quadratic equations be solved using the quadratic formula?
A2: Yes, the quadratic formula provides a solution for any quadratic equation, regardless of whether the roots are real or complex.
Q3: What is the significance of complex conjugate pairs?
A3: When dealing with polynomials with real coefficients, complex roots always come in conjugate pairs. This means if a + bi is a root, then a - bi is also a root.
Conclusion
Solving the quadratic equation x² + 3x + 10 = 0 leads us into the fascinating world of complex numbers. While initially seeming counterintuitive, complex numbers are essential tools in numerous scientific and engineering disciplines. This problem underscores the importance of understanding different methods for solving quadratic equations and the broader mathematical landscape they reveal. Mastering these concepts provides a solid foundation for tackling more advanced mathematical challenges in various fields. The seemingly simple equation x² + 3x + 10 = 0 opens a door to a far richer and more complex understanding of mathematics itself.
Latest Posts
Latest Posts
-
Differentiate Between Taxonomy And Systematics
Sep 12, 2025
-
Formula For Efficiency In Physics
Sep 12, 2025
-
Sodium Hydroxide Vs Potassium Hydroxide
Sep 12, 2025
-
Platinum 100 Ohm Rtd Chart
Sep 12, 2025
-
Convert Into Mixed Fraction 30 7
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X2 3x 10 0 Solution . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.