X 4 5 X 10
thesills
Sep 18, 2025 · 6 min read
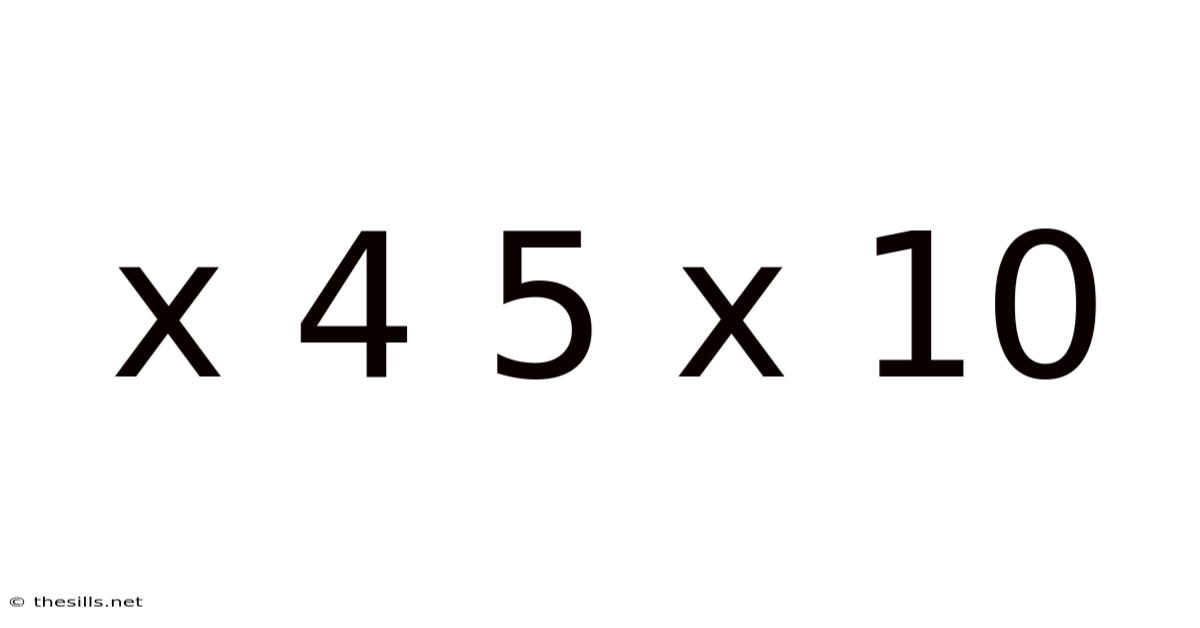
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x 4 5 x 10"
This article delves into the seemingly simple yet surprisingly multifaceted mathematical expression "x 4 5 x 10." While it may appear straightforward at first glance, its interpretation and application depend heavily on context and the intended operation. We will explore various interpretations, offering a comprehensive understanding of this expression, clarifying ambiguities, and demonstrating its use in different mathematical scenarios. Understanding this seemingly basic equation provides a foundational understanding of order of operations and algebraic manipulation.
Understanding the Ambiguity: Order of Operations is Key
The core challenge with "x 4 5 x 10" lies in its inherent ambiguity. Without parentheses or explicitly defined operators, the order in which the operations are performed significantly impacts the final result. This ambiguity highlights the critical importance of order of operations, also known as PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These mnemonics dictate the sequence of operations: calculations within parentheses are performed first, followed by exponents, then multiplication and division (from left to right), and finally addition and subtraction (from left to right).
Interpretation 1: Sequential Multiplication
One possible interpretation is to perform the multiplications sequentially from left to right. Assuming 'x' represents a variable or an unknown number, this interpretation would yield:
(x * 4) * 5 * 10 = 200x
This simplifies the expression to 200 times the value of x. If, for instance, x = 2, the result would be 400. This interpretation prioritizes a straightforward, linear approach to the calculation.
Interpretation 2: Grouping and Multiplication
Another interpretation could involve grouping the numbers:
x * (4 * 5 * 10) = 200x
This interpretation groups the constants together before multiplying them with 'x'. This produces the same result as the sequential multiplication method, highlighting that in this specific case, the grouping doesn't affect the outcome. However, this is not always true, as we'll see in subsequent examples.
Interpretation 3: Introducing Variables and Algebraic Manipulation
Let's introduce another variable, 'y', and rewrite the expression as:
x * 4 * 5 * 10 = y
In this scenario, the expression becomes an equation where we need to solve for either x or y, depending on the given information. For example, if y = 1000, we can solve for x:
x * 4 * 5 * 10 = 1000 200x = 1000 x = 1000 / 200 x = 5
This example demonstrates how the expression "x 4 5 x 10" can be used within a broader mathematical context, involving algebraic manipulation to find the value of an unknown variable.
Interpretation 4: Considering Implicit Multiplication and Context
The absence of explicit multiplication symbols (×) between 'x' and the numbers could also lead to varied interpretations depending on the context. In certain programming languages or mathematical notations, juxtaposition can imply multiplication. For instance, if 'x' is a matrix or a vector, 'x45' might represent a scalar multiplication or matrix-vector multiplication, depending on the dimensions and rules of the specific mathematical system.
In this case, the expression "x 4 5 x 10" would need to be interpreted within the given framework. Without further context, it's impossible to provide a definitive answer.
The Importance of Parentheses and Clarity
The ambiguity highlighted above underscores the vital role of parentheses in clarifying mathematical expressions. Using parentheses can eliminate any doubt regarding the order of operations. For instance:
- (x * 4) * (5 * 10): This clearly indicates that (5 * 10) should be calculated first, followed by the multiplication with (x * 4).
- x * (4 * 5 * 10): This explicitly groups the constants together for multiplication with x.
- ((x * 4) * 5) * 10: This clarifies a step-by-step sequential multiplication.
The use of parentheses makes the intended order of operations unambiguous, reducing the potential for misinterpretation and ensuring accurate calculations.
Expanding the Scope: Real-World Applications
While this seemingly simple expression might appear confined to abstract mathematical exercises, its principles have real-world implications. Understanding order of operations is crucial in various fields, including:
- Computer Programming: Programmers rely heavily on order of operations to ensure accurate computation within their code. Misinterpretations can lead to unexpected results and program errors.
- Engineering and Physics: Many engineering and physics calculations involve complex equations where the order of operations is critical for obtaining correct results. Errors in this area can have significant consequences.
- Finance and Accounting: Financial calculations, such as compound interest or discount calculations, rely on the correct order of operations to determine accurate figures.
- Data Analysis and Statistics: Accurate data analysis and statistical calculations depend heavily on correctly applying the order of operations.
Beyond the Basics: Advanced Mathematical Concepts
The principles illustrated in analyzing "x 4 5 x 10" extend to more advanced mathematical concepts. For instance, the understanding of order of operations is fundamental to:
- Linear Algebra: In linear algebra, the order of matrix multiplication significantly affects the result.
- Calculus: The order of operations is crucial when performing calculations involving derivatives and integrals.
- Abstract Algebra: Abstract algebra often deals with operations that don't follow the standard PEMDAS rules, requiring a deeper understanding of operational precedence.
Frequently Asked Questions (FAQ)
Q1: What is the most common interpretation of "x 4 5 x 10"?
A1: In the absence of parentheses or additional context, the most common interpretation is sequential multiplication from left to right: (x * 4) * 5 * 10 = 200x.
Q2: Can the expression be simplified further?
A2: Yes, without knowing the value of x, the expression can be simplified to 200x. If a value for x is provided, it can be calculated to a single numerical value.
Q3: What happens if 'x' represents a matrix or vector?
A3: The interpretation would change significantly, depending on the specific rules and dimensions within the context of matrix or vector algebra. The expression would need to be evaluated according to the rules governing matrix and vector multiplication.
Q4: Why is understanding order of operations important?
A4: Understanding order of operations is crucial for performing accurate calculations in various mathematical and real-world contexts. Errors in applying the order of operations can lead to incorrect results with significant consequences.
Conclusion: The Power of Precision in Mathematics
The seemingly simple mathematical expression "x 4 5 x 10" highlights the critical importance of precision and clarity in mathematical notation. The ambiguity inherent in the expression emphasizes the need for explicit use of parentheses to define the order of operations. Understanding order of operations is not merely a rule to follow; it's a fundamental principle that underlies many mathematical and scientific fields. By carefully examining the various interpretations and applications of this simple expression, we gain a deeper appreciation for the nuances of mathematical language and the importance of clear communication in ensuring accurate and reliable results. Mastering these fundamental concepts lays the groundwork for tackling more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
Is Pbl2 Soluble In Water
Sep 18, 2025
-
What Metal Is Most Reactive
Sep 18, 2025
-
Hardest Part In Our Body
Sep 18, 2025
-
Lewis Dot Structure For Methane
Sep 18, 2025
-
Moment Of Inertia Of Cube
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 4 5 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.