X 3 Y 4 1
thesills
Sep 17, 2025 · 6 min read
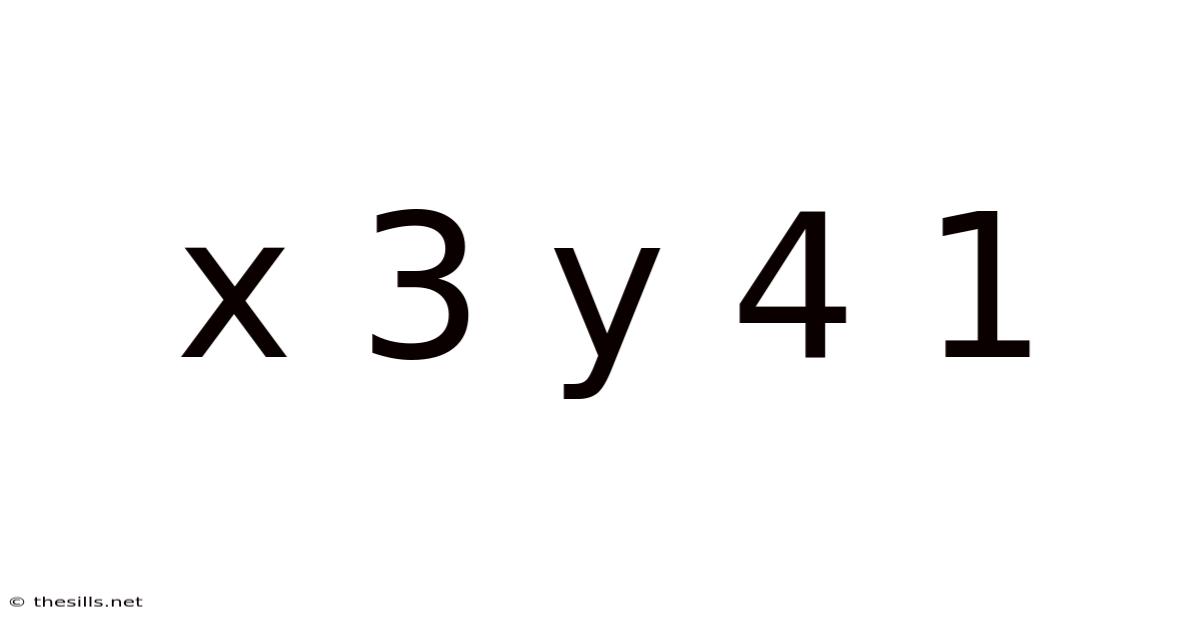
Table of Contents
Decoding the Enigma: A Deep Dive into x³y⁴ + 1
This article explores the mathematical expression x³y⁴ + 1, delving into its properties, potential applications, and the broader mathematical concepts it represents. We'll move beyond a simple surface-level understanding, examining its behavior under different conditions and revealing its hidden complexities. This seemingly straightforward algebraic expression offers a gateway to understanding polynomial functions, factorization techniques, and even the fundamental theorem of algebra. Prepare to embark on a journey into the fascinating world of higher-order polynomials!
Introduction: Understanding the Basics
At first glance, x³y⁴ + 1 appears simple. It's a polynomial expression, meaning it's a combination of variables (x and y) and constants (1) involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. The terms "x³" and "y⁴" represent x raised to the power of 3 and y raised to the power of 4 respectively. The "1" is a constant term. This seemingly simple expression, however, holds a wealth of mathematical significance. We will explore various aspects, from its graphical representation to its potential use in more advanced mathematical contexts. Understanding this foundational expression paves the way for understanding more complex mathematical concepts.
Exploring the Polynomial's Behavior
The expression x³y⁴ + 1 is a multivariate polynomial, meaning it involves more than one variable. Its degree is determined by the highest sum of exponents in any term. In this case, the degree is 7 (3 + 4). This degree dictates many of the polynomial's properties, particularly concerning its graphical representation and the number of potential roots.
Let's consider how the expression behaves under different circumstances:
-
When x = 0: The expression simplifies to 1, regardless of the value of y. This indicates a horizontal asymptote at y = 1 when x approaches 0.
-
When y = 0: The expression simplifies to x³ + 1. This is a cubic polynomial with one real root at x = -1 and two complex roots. This highlights the shift from a multivariate to a univariate function when one variable is fixed.
-
When x and y are both large positive numbers: The term x³y⁴ dominates, and the expression grows rapidly.
-
When x and y are both large negative numbers: The term x³y⁴ will be positive if the exponents are even, leading to large positive values of the function.
Graphical Representation and Visualization
Visualizing this expression requires a three-dimensional graph, as it involves two independent variables (x and y) and one dependent variable (the value of the expression). The graph would be a surface in three-dimensional space. Creating such a graph can be done using mathematical software packages like MATLAB, Mathematica, or specialized graphing calculators. The resulting surface would showcase how the value of the expression changes with variations in x and y. We would see a relatively flat area near the origin (x=0, y=0), and a steep increase in the value of the expression as x and y move away from the origin, especially in the positive quadrants. Understanding this graphical representation enhances intuitive understanding of the expression's behavior.
Factorization and Root Finding
Factoring this polynomial is a more challenging task. Simple factorization techniques may not yield immediate results. While x³y⁴ + 1 doesn't have readily apparent factors, exploring advanced factorization methods might reveal hidden structures. Note that the Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots (considering multiplicity and complex roots). In our case, the polynomial has a degree of 7, thus possessing seven roots in the complex plane. Locating these roots analytically would be a significantly complex endeavor, requiring advanced mathematical techniques. Numerical methods, like Newton-Raphson, are often employed to approximate the roots of such high-degree polynomials.
Applications and Connections to Other Mathematical Concepts
While x³y⁴ + 1 might seem abstract, it finds connections with several important mathematical concepts:
-
Polynomial Approximation: Polynomials are extensively used to approximate complex functions. Understanding the properties of simpler polynomials like x³y⁴ + 1 provides a foundation for working with more intricate approximations.
-
Multivariate Calculus: The expression becomes relevant in multivariate calculus when considering partial derivatives with respect to x and y.
-
Numerical Analysis: Numerical methods for solving equations and approximating functions often involve polynomials. Our expression provides a good example to test and refine these methods.
-
Abstract Algebra: This expression can be explored within the context of polynomial rings and ideals in abstract algebra. This branch of mathematics delves into the structure and properties of polynomials and provides a more formal and rigorous framework to explore such functions.
Advanced Considerations and Further Exploration
The exploration of x³y⁴ + 1 can be extended in several directions:
-
Modulus Arithmetic: Examining the expression modulo a given integer (e.g., modulo 2, modulo 3) can reveal interesting patterns and properties.
-
Series Expansion: Power series expansions could be used to represent the expression, providing alternative ways to approximate its value.
-
Differential Equations: The expression could potentially appear in certain differential equations, making it relevant in the study of dynamical systems.
Frequently Asked Questions (FAQ)
Q: Is there a simple way to factor x³y⁴ + 1?
A: No, there's no simple, readily apparent factorization for x³y⁴ + 1. Advanced factorization techniques or numerical methods might be required to find its roots.
Q: What is the significance of the "+1" in the expression?
A: The "+1" term is crucial. Without it, the expression would be simpler to factor and analyze. The constant term impacts the overall behavior of the polynomial, including its roots and its graphical representation.
Q: Can this expression be used in real-world applications?
A: While not directly used in everyday applications, understanding its properties contributes to the foundation of mathematical tools used in many fields, such as computer graphics, physics simulations, and engineering modeling.
Q: How would I graph this in a 3D plotting software?
A: You would define the function z = x³y⁴ + 1 and plot it as a 3D surface using software like MATLAB, Mathematica, or similar programs.
Conclusion: The Enduring Significance of Simplicity
The seemingly simple expression x³y⁴ + 1 offers a rich and engaging exploration into the world of higher-order polynomials. Its analysis touches on various mathematical concepts, from basic algebra to advanced topics in calculus, numerical analysis, and abstract algebra. While its direct applications might not be immediately obvious, the knowledge and skills gained from studying this expression contribute significantly to a deeper understanding of mathematics as a whole. The journey of unraveling its complexities serves as a testament to the power and beauty of mathematical inquiry – even within a seemingly simple formula, hidden depths await those willing to explore. Continue to explore, question, and delve deeper into the world of mathematics – the rewards are immeasurable.
Latest Posts
Latest Posts
-
Advantages Of 4 Chambered Heart
Sep 17, 2025
-
Centre Of Mass Of Rod
Sep 17, 2025
-
Difficult Chemical Equations To Balance
Sep 17, 2025
-
What Is The Lightest Liquid
Sep 17, 2025
-
Derivative Of X 1 X
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about X 3 Y 4 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.