X 3 3x 2 3
thesills
Sep 13, 2025 · 5 min read
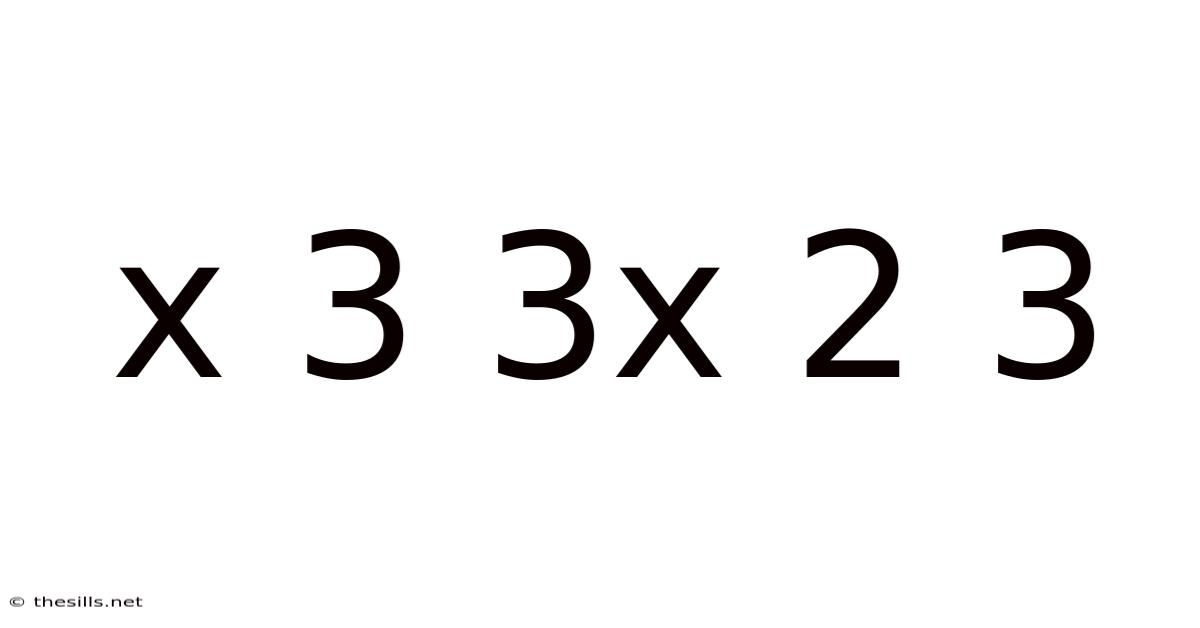
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x³ + 3x² + 3x + 1"
This article delves into the fascinating mathematical expression x³ + 3x² + 3x + 1, exploring its meaning, derivation, applications, and related concepts. We will unravel its secrets, revealing its connection to binomial expansion and its significance in various fields, from simple algebra to advanced calculus. Understanding this expression provides a solid foundation for grasping more complex mathematical principles.
Introduction: Unpacking the Polynomial
The expression x³ + 3x² + 3x + 1 is a polynomial – a mathematical expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Specifically, it's a cubic polynomial because the highest power of the variable x is 3. This seemingly simple expression holds a wealth of mathematical significance, particularly its relationship to the binomial theorem. We will uncover this connection and explore its implications.
Understanding Binomial Expansion
Before we dive into the specifics of x³ + 3x² + 3x + 1, let's refresh our understanding of the binomial theorem. The binomial theorem provides a formula for expanding expressions of the form (a + b)ⁿ, where 'n' is a non-negative integer. The expansion is given by:
(a + b)ⁿ = Σ [n! / (k!(n-k)!)] * a⁽ⁿ⁻ᵏ⁾ * bᵏ (where k ranges from 0 to n)
This might look daunting, but it's simpler than it seems. The key is understanding the binomial coefficients, represented by [n! / (k!(n-k)!)] which are often written as "n choose k" or ⁿCₖ. These coefficients represent the number of ways to choose k items from a set of n items.
Let's look at a few examples:
- (a + b)¹ = a + b
- (a + b)² = a² + 2ab + b²
- (a + b)³ = a³ + 3a²b + 3ab² + b³
- (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
Notice a pattern emerging? The coefficients correspond to Pascal's Triangle, a visual representation of binomial coefficients.
Connecting the Dots: x³ + 3x² + 3x + 1 and Binomial Expansion
Now, let's return to our original expression: x³ + 3x² + 3x + 1. If we compare this to the binomial expansion of (a + b)³, we see a striking resemblance. In fact, x³ + 3x² + 3x + 1 is the expansion of (x + 1)³:
(x + 1)³ = x³ + 3x²(1) + 3x(1)² + 1³ = x³ + 3x² + 3x + 1
This connection is crucial. It means our seemingly complex cubic polynomial is actually a simple perfect cube. This simplification opens doors to numerous applications and easier manipulations.
Applications and Significance
The expression x³ + 3x² + 3x + 1, being equivalent to (x + 1)³, finds applications in various mathematical contexts:
-
Algebraic Simplification: Recognizing this as a perfect cube allows for significant simplification in algebraic expressions. This can greatly reduce the complexity of problems involving factoring, solving equations, and performing other algebraic manipulations.
-
Calculus: In calculus, understanding this relationship is critical when dealing with differentiation and integration. Finding the derivative or integral of (x+1)³ is far simpler than working directly with the expanded form x³ + 3x² + 3x + 1.
-
Geometry: This expression can appear in geometric problems involving volumes of cubes or related three-dimensional shapes. Understanding its expansion can help in relating the side length of a cube to its volume.
-
Number Theory: When dealing with integer values of x, the expression relates to the sums of cubes and their properties within number theory.
-
Computer Science: This factorization can lead to more efficient algorithms in computational tasks involving polynomial manipulations.
Solving Equations involving x³ + 3x² + 3x + 1
The fact that x³ + 3x² + 3x + 1 = (x + 1)³ greatly simplifies the process of solving equations involving this polynomial. For instance, consider the equation:
x³ + 3x² + 3x + 1 = 8
By recognizing the left-hand side as (x + 1)³, we can rewrite the equation as:
(x + 1)³ = 8
Taking the cube root of both sides, we get:
x + 1 = 2
Therefore, x = 1. This is a significantly simpler solution compared to attempting to solve the cubic equation directly using more complex methods.
Beyond the Basics: Exploring Generalizations
The concept extends beyond (x + 1)³. We can apply the binomial theorem to any binomial raised to an integer power. This allows us to understand and simplify numerous polynomials. For example:
(x + 2)³ = x³ + 6x² + 12x + 8
(x - 1)⁴ = x⁴ - 4x³ + 6x² - 4x + 1
These expressions, while more complex, are still fundamentally derived from the binomial theorem and can be simplified and manipulated using similar techniques.
Frequently Asked Questions (FAQ)
-
Q: What is the significance of the coefficients 1, 3, 3, 1?
- A: These coefficients are the binomial coefficients from the expansion of (a+b)³, specifically ³C₀, ³C₁, ³C₂, and ³C₃, which are 1, 3, 3, and 1 respectively. They appear in Pascal's Triangle.
-
Q: Can this expression be factored in other ways?
- A: While it can be factored as (x + 1)³, this is the most fundamental and useful factorization. Other factorizations might exist but would be less insightful.
-
Q: What if the expression was x³ + 3x² + 3x + 2?
- A: This expression is not a perfect cube. It would require different factorization techniques to solve equations or simplify expressions involving it.
-
Q: How does this relate to complex numbers?
- A: The binomial theorem and its applications extend to complex numbers as well. Understanding this foundation is important when dealing with complex polynomials.
Conclusion: A Foundation for Further Exploration
The seemingly simple polynomial x³ + 3x² + 3x + 1, equivalent to (x + 1)³, is a powerful illustration of the binomial theorem and its applications. Understanding its expansion and its connection to perfect cubes provides a strong foundation for tackling more complex algebraic and calculus problems. Its significance extends across various mathematical domains, highlighting the interconnectedness of mathematical concepts. By mastering this concept, you'll gain a deeper appreciation for the elegance and power of mathematical principles and their real-world applications. This exploration serves as a springboard for delving into more advanced concepts within algebra, calculus, and other related mathematical fields.
Latest Posts
Latest Posts
-
What Does Nearest Degree Mean
Sep 13, 2025
-
Large Gland In Human Body
Sep 13, 2025
-
Provides Support For The Cell
Sep 13, 2025
-
Definition Of Gross Primary Production
Sep 13, 2025
-
Are Amoebas Prokaryotic Or Eukaryotic
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.