X 2 X 3 2
thesills
Sep 14, 2025 · 5 min read
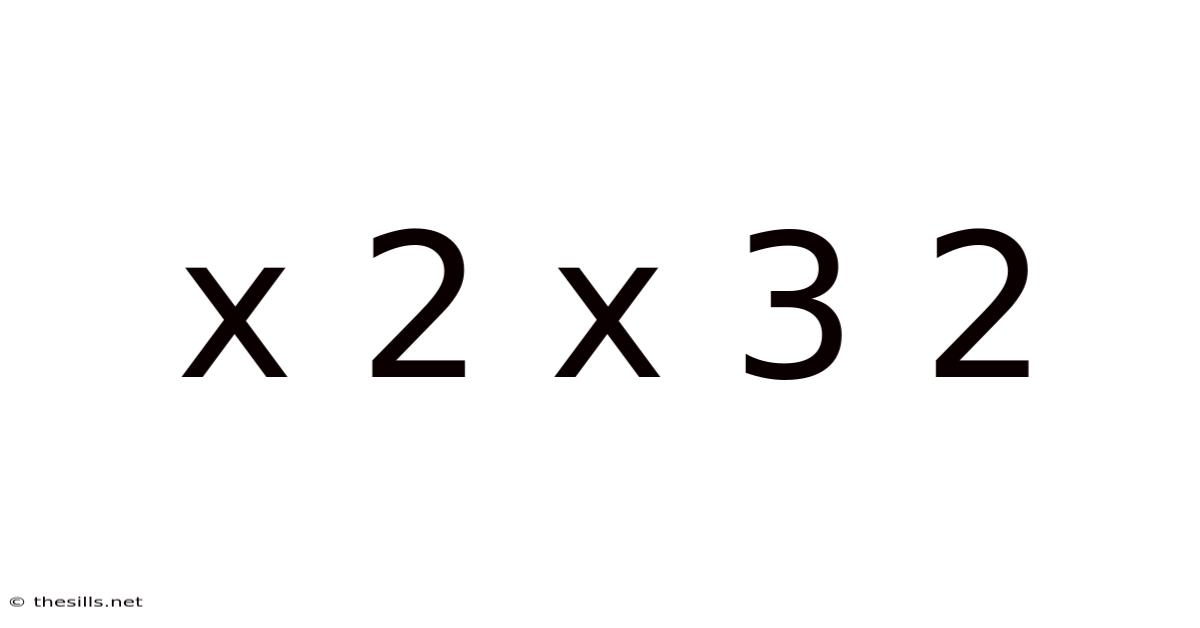
Table of Contents
Decoding the Enigma: A Deep Dive into x²x³²
The expression "x²x³²" might seem initially daunting, particularly to those less familiar with algebraic manipulation. However, this seemingly complex expression is actually quite straightforward once we understand the fundamental rules governing exponents and algebraic simplification. This article will serve as a comprehensive guide, unraveling the mysteries behind this expression, exploring its underlying principles, and providing a clear, step-by-step explanation suitable for learners of all levels. We'll cover the basics of exponents, delve into the specific simplification process for this expression, and address common questions and misconceptions.
Introduction: Understanding Exponents and Their Properties
Before tackling "x²x³²", let's establish a solid foundation in exponential notation. An exponent, or power, indicates how many times a base number is multiplied by itself. For instance, x³ means x * x * x. The key properties of exponents are crucial for simplifying expressions:
- Product of Powers: When multiplying terms with the same base, we add the exponents. This is represented as xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾. For example, x² * x³ = x⁽²⁺³⁾ = x⁵.
- Power of a Power: When raising a power to another power, we multiply the exponents. This is represented as (xᵃ)ᵇ = x⁽ᵃᵇ⁾. For example, (x²)³ = x⁽²³⁾ = x⁶.
- Quotient of Powers: When dividing terms with the same base, we subtract the exponents. This is represented as xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾, where x ≠ 0. For example, x⁵ / x² = x⁽⁵⁻²⁾ = x³.
- Zero Exponent: Any non-zero base raised to the power of zero equals 1. This is represented as x⁰ = 1, where x ≠ 0.
- Negative Exponent: A negative exponent indicates a reciprocal. This is represented as x⁻ⁿ = 1/xⁿ, where x ≠ 0. For example, x⁻² = 1/x².
These properties form the bedrock of simplifying exponential expressions and are essential for understanding our target expression: x²x³².
Simplifying x²x³²: A Step-by-Step Approach
Now, let's apply our understanding of exponential properties to simplify "x²x³²". The expression represents the multiplication of two terms with the same base, x. Therefore, we can directly apply the "product of powers" rule:
-
Identify the Base and Exponents: Our base is x. The exponents are 2 and 32.
-
Apply the Product of Powers Rule: According to the rule, when multiplying terms with the same base, we add the exponents. Thus, x² * x³² = x⁽²⁺³²⁾.
-
Perform the Addition: Adding the exponents, we get 2 + 32 = 34.
-
Final Simplified Expression: Therefore, the simplified form of x²x³² is x³⁴.
Explanation of the Simplification: A Deeper Dive
The simplification process leverages the fundamental concept that multiplication is repeated addition. When we multiply x² by x³², we are essentially multiplying:
(x * x) * (x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x * x)
Counting the total number of x's, we find there are 34 instances. This directly corresponds to the result we obtained using the product of powers rule: x³⁴. This demonstrates the elegance and efficiency of using exponential rules for simplifying such expressions. The use of exponents greatly reduces the complexity and length of the expression while maintaining its mathematical accuracy.
Common Misconceptions and Their Clarifications
Several common misconceptions can arise when dealing with exponential expressions. Let's address some of them:
-
Incorrectly Multiplying Exponents: A frequent mistake is to multiply the exponents instead of adding them when multiplying terms with the same base. Remember, xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾, not x⁽ᵃ*ᵇ⁾.
-
Confusing Bases: The product of powers rule only applies when the bases are the same. x² * y³ cannot be simplified further because the bases (x and y) are different.
-
Ignoring Order of Operations: The order of operations (PEMDAS/BODMAS) must always be followed. Exponents are evaluated before multiplication or division.
Further Exploration: Expanding the Concept
While we've focused on the specific expression x²x³², the principles discussed extend to more complex scenarios involving multiple terms and various exponents, both positive and negative. The same rules – the product of powers, power of a power, etc. – will always apply. Consider, for example, the expression (x²y³)⁴. We would first apply the power of a power rule to each term within the parentheses, resulting in x⁸y¹², demonstrating the versatility and wide applicability of these fundamental exponential properties.
Frequently Asked Questions (FAQ)
- Q: What if the exponents were negative?
A: The process remains the same. For instance, x⁻² * x³ = x⁽⁻²⁺³⁾ = x¹. Remember that a negative exponent represents a reciprocal.
- Q: Can I simplify x²x³² if x represents a specific number, say 2?
A: Yes, absolutely. Substitute x with 2, resulting in 2² * 2³² = 2³⁴. Then, you can calculate the numerical value of 2³⁴ using a calculator.
- Q: What if there were more terms with the same base, like x²x³²x⁵?
A: Simply extend the process. Add all the exponents: 2 + 32 + 5 = 39, resulting in x³⁹.
Conclusion: Mastering the Fundamentals of Exponents
Understanding exponential notation and its associated properties is crucial for success in algebra and beyond. The seemingly complex expression x²x³² simplifies elegantly to x³⁴ using the straightforward application of the product of powers rule. By mastering these fundamental concepts, you can confidently tackle more intricate algebraic expressions and build a strong foundation in mathematical reasoning. Remember to practice regularly, apply the rules consistently, and address any misconceptions proactively to further strengthen your understanding and problem-solving abilities. The journey of mastering algebra is a rewarding one, filled with the satisfaction of unraveling mathematical puzzles and gaining a deeper appreciation for the underlying logic and structure of mathematics.
Latest Posts
Latest Posts
-
Ionic Compounds Containing Polyatomic Ions
Sep 14, 2025
-
Geometrical Meaning Of Scalar Product
Sep 14, 2025
-
Element With Atomic Number 15
Sep 14, 2025
-
Where Is Shifting Cultivation Practiced
Sep 14, 2025
-
Sodium Chloride Density G Ml
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.