X 2 X 1 Simplify
thesills
Sep 15, 2025 · 5 min read
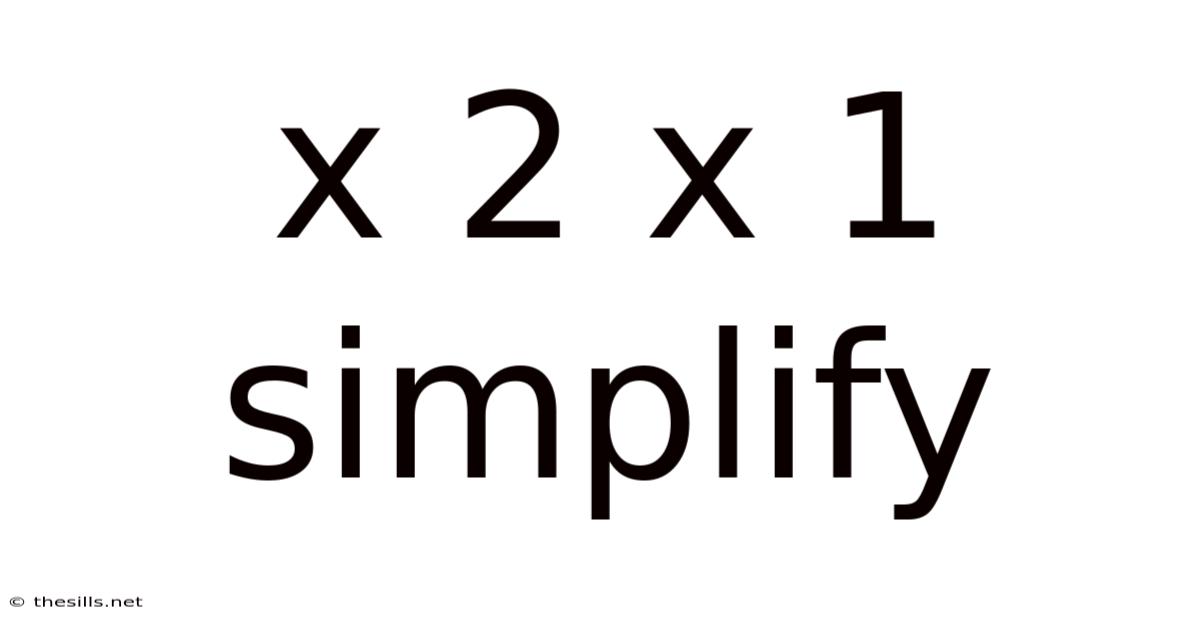
Table of Contents
Simplifying x² x 1: A Deep Dive into Algebraic Expressions
Understanding how to simplify algebraic expressions is a fundamental skill in mathematics. This article will provide a comprehensive guide to simplifying the expression x² x 1, exploring its underlying principles, demonstrating the process step-by-step, and addressing common questions and misconceptions. We will delve into the core concepts of algebra, focusing on the properties of exponents and multiplication, ensuring a clear and thorough understanding for learners of all levels. This guide is designed to be easily understood, even by those with limited prior algebra experience, while also offering deeper insights for more advanced students.
Introduction to Algebraic Expressions
Algebraic expressions are mathematical phrases that combine numbers, variables, and operations (+, -, ×, ÷). Variables, typically represented by letters like x, y, or z, represent unknown quantities. Simplifying an algebraic expression means rewriting it in its most concise and efficient form, without changing its value. This often involves combining like terms and applying rules of arithmetic and algebra.
Our target expression, x² x 1, is a simple yet illustrative example of this process. It combines a variable raised to a power (x²), a multiplication operation, and a constant (1). Understanding how to simplify this expression will lay a solid foundation for tackling more complex algebraic problems.
Step-by-Step Simplification of x² x 1
The key to simplifying x² x 1 lies in understanding the properties of multiplication involving numbers and variables. Let's break down the simplification process step-by-step:
Step 1: Understanding the Components
- x²: This represents x multiplied by itself (x * x). The '2' is called the exponent or power, indicating the number of times the base (x) is multiplied by itself.
- x: This is simply the variable x. It can be thought of as x¹, where the exponent '1' is often omitted.
- 1: This is a constant, a numerical value that does not change.
Step 2: Applying the Multiplicative Identity Property
The multiplicative identity property states that any number multiplied by 1 remains unchanged. In other words, a x 1 = a, for any number 'a'. This property is crucial for simplifying our expression.
Therefore, x² x 1 = x².
Step 3: The Final Simplified Expression
The simplified form of x² x 1 is simply x². There are no like terms to combine, and the multiplicative identity property allows us to eliminate the 'x 1' component.
Deeper Dive: Properties of Exponents and Multiplication
To further solidify our understanding, let's explore the relevant properties of exponents and multiplication.
-
Commutative Property of Multiplication: The order of factors in multiplication does not affect the product. This means a x b = b x a. In our case, this allows us to rewrite x² x 1 as 1 x x².
-
Associative Property of Multiplication: The grouping of factors in multiplication does not affect the product. This means (a x b) x c = a x (b x c). This property is particularly useful when dealing with more complex expressions involving multiple variables and constants.
-
Exponent Rules: When multiplying terms with the same base, we add the exponents. For example, x² x x³ = x⁽²⁺³⁾ = x⁵. While not directly applicable in simplifying x² x 1 (since we are multiplying by x⁰ which is 1), understanding this rule is crucial for tackling more advanced problems.
Illustrative Examples with Different Variables and Constants
Let's consider similar expressions to further illustrate the simplification process:
- y³ x 1: Applying the multiplicative identity property, this simplifies to y³.
- (2a²) x 1: This simplifies to 2a². The constant '2' remains unaffected by multiplying by 1.
- (3x²y) x 1: This simplifies to 3x²y. The coefficients and variables remain unchanged.
Addressing Common Misconceptions
A common misunderstanding is that multiplying by 1 somehow "disappears" the variable. It's crucial to understand that multiplying by 1 does not change the value of the expression; it simply preserves the original expression in its simplest form.
Another potential confusion could arise if students are not familiar with the multiplicative identity property. A strong grasp of fundamental algebraic properties is key to avoiding errors.
Expanding on the Concept: Polynomials and Further Simplification
While x² x 1 represents a simple algebraic expression, the principles involved are fundamental to working with more complex expressions like polynomials. Polynomials are algebraic expressions consisting of multiple terms, each term being a product of constants and variables raised to non-negative integer powers. Simplifying polynomials often involves combining like terms (terms with the same variables raised to the same powers).
For instance, consider the polynomial 3x² + 2x + 5x² - x. We can simplify this by combining like terms:
(3x² + 5x²) + (2x - x) = 8x² + x
This example highlights the importance of understanding the basic principles of simplification, which are the building blocks for tackling more advanced mathematical concepts.
Frequently Asked Questions (FAQ)
Q1: What if the expression was x² x 0?
A1: Any number multiplied by zero equals zero. Therefore, x² x 0 = 0. This is a different scenario, governed by the multiplicative property of zero.
Q2: How does this relate to solving equations?
A2: Simplifying algebraic expressions is a crucial preliminary step in solving equations. Simplifying the equation before attempting to solve it makes the process much easier and less prone to errors.
Q3: Are there any cases where x² x 1 would not simplify to x²?
A3: No, in the context of standard algebraic operations, x² x 1 will always simplify to x².
Q4: Can this concept be applied to more complex expressions involving fractions?
A4: Yes, absolutely. The multiplicative identity property applies to all real numbers, including fractions. For example, (x²/2) x 1 = x²/2. The principles remain the same.
Conclusion: Mastering the Fundamentals of Algebra
Simplifying algebraic expressions, such as x² x 1, is a foundational skill in mathematics. Understanding the multiplicative identity property and the basic properties of exponents is crucial for mastering algebraic manipulation. This process, seemingly simple at first glance, underpins more complex algebraic operations and problem-solving. By grasping these fundamental concepts, students build a solid foundation for tackling more challenging mathematical concepts in the future. The ability to simplify expressions efficiently and accurately is essential for success in algebra and beyond. Consistent practice and a clear understanding of the underlying principles are key to developing proficiency in simplifying algebraic expressions and mastering the basics of algebra.
Latest Posts
Latest Posts
-
How To Make Accordion Book
Sep 16, 2025
-
Silver Nitrate With Potassium Chloride
Sep 16, 2025
-
Middle Letter In The Alphabet
Sep 16, 2025
-
Ammonium Chloride Basic Or Acidic
Sep 16, 2025
-
Ratio Of Dihybrid Test Cross
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 1 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.