X 2 6x 25 0
thesills
Sep 15, 2025 · 6 min read
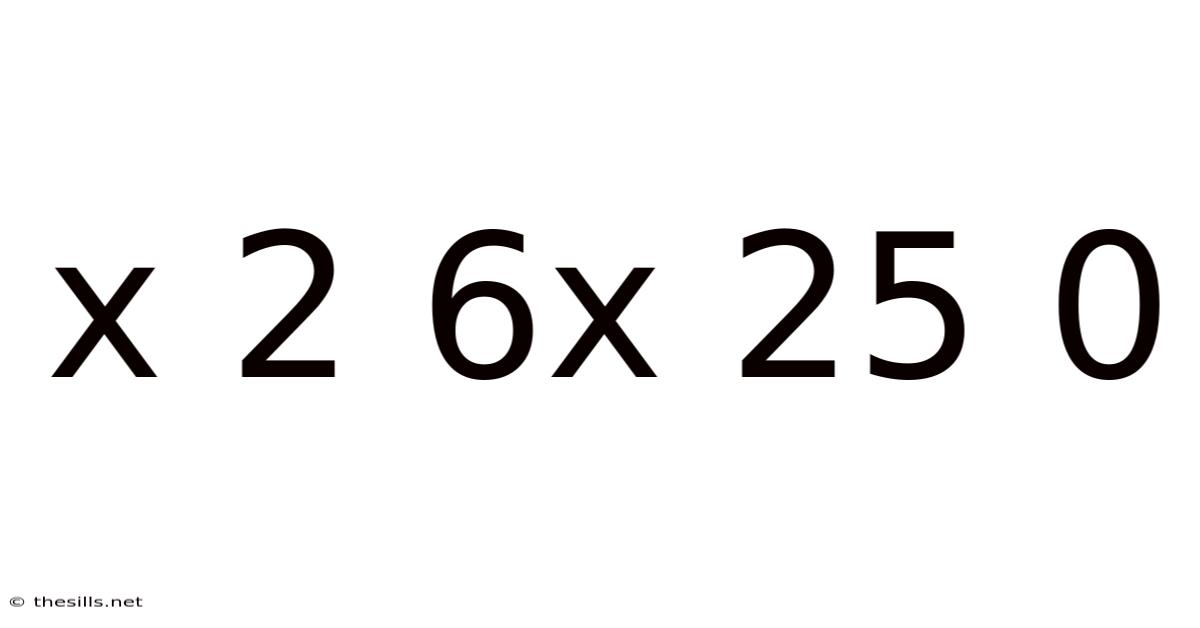
Table of Contents
Decoding the Mathematical Expression: x² + 6x + 25 = 0
This article delves into the mathematical expression x² + 6x + 25 = 0, exploring its nature, solving methods, and implications. We'll move beyond a simple solution and investigate the broader context of quadratic equations, their graphical representation, and the significance of complex numbers in mathematics. Understanding this seemingly simple equation unlocks a deeper appreciation for fundamental algebraic concepts.
Introduction: Understanding Quadratic Equations
The equation x² + 6x + 25 = 0 is a quadratic equation. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (x in this case) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. In our specific equation, a = 1, b = 6, and c = 25.
Quadratic equations are fundamental to many areas of mathematics and science, appearing in physics, engineering, and computer science, amongst others. They describe parabolic trajectories, model projectile motion, and are used in optimization problems. Solving quadratic equations is a crucial skill for anyone pursuing studies in STEM fields.
Methods for Solving Quadratic Equations
Several methods exist for solving quadratic equations. Let's examine the most common ones and apply them to x² + 6x + 25 = 0.
-
Factoring: This method involves expressing the quadratic expression as a product of two linear expressions. However, not all quadratic equations can be factored easily using real numbers. In our case, x² + 6x + 25 cannot be factored using real numbers because there are no two real numbers that add up to 6 and multiply to 25.
-
Quadratic Formula: This is a general formula that provides the solutions for any quadratic equation, regardless of whether it can be factored easily. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 6, c = 25), we get:
x = [-6 ± √(6² - 4 * 1 * 25)] / 2 * 1 x = [-6 ± √(36 - 100)] / 2 x = [-6 ± √(-64)] / 2
Notice that we have a negative number under the square root. This indicates that the solutions to this equation are complex numbers.
-
Completing the Square: This method involves manipulating the equation to create a perfect square trinomial. While effective, it's often less efficient than the quadratic formula for equations that don't readily factor. For our example:
x² + 6x + 25 = 0 x² + 6x = -25 x² + 6x + 9 = -25 + 9 (Adding (b/2)² = (6/2)² = 9 to both sides) (x + 3)² = -16 x + 3 = ±√(-16) x = -3 ± 4i (where 'i' represents the imaginary unit, √(-1))
Understanding Complex Numbers
The solutions we obtained using both the quadratic formula and completing the square involve the imaginary unit, i, where i² = -1. These are complex numbers, which are numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. The solutions to x² + 6x + 25 = 0 are x = -3 + 4i and x = -3 - 4i. These are complex conjugates, meaning they differ only in the sign of the imaginary part.
Complex numbers are essential in various branches of mathematics, physics, and engineering. They are crucial in representing alternating current circuits, quantum mechanics, and signal processing. Initially, they might seem abstract, but their practical applications are significant.
Graphical Representation of Quadratic Equations
Quadratic equations represent parabolas when graphed on a Cartesian coordinate system. The parabola's vertex, axis of symmetry, and direction (opening upwards or downwards) are determined by the coefficients a, b, and c. Since our equation has no real roots (the discriminant, b² - 4ac = -64, is negative), the parabola does not intersect the x-axis. This means the parabola lies entirely above the x-axis (because the coefficient 'a' is positive).
The vertex of the parabola can be found using the formula:
x = -b / 2a = -6 / (2 * 1) = -3
Substituting x = -3 into the equation gives the y-coordinate of the vertex:
y = (-3)² + 6(-3) + 25 = 9 - 18 + 25 = 16
Therefore, the vertex of the parabola is (-3, 16). The parabola opens upwards, and its minimum value is 16.
Discriminant and Nature of Roots
The expression b² - 4ac, known as the discriminant, determines the nature of the roots (solutions) of a quadratic equation.
- If b² - 4ac > 0, the equation has two distinct real roots. The parabola intersects the x-axis at two points.
- If b² - 4ac = 0, the equation has one real root (a repeated root). The parabola touches the x-axis at one point (the vertex).
- If b² - 4ac < 0, the equation has two complex conjugate roots. The parabola does not intersect the x-axis.
In our case, b² - 4ac = -64 < 0, which confirms that the equation has two complex conjugate roots, as we already found.
Applications of Quadratic Equations
The applications of quadratic equations are vast and span multiple disciplines:
- Physics: Projectile motion, calculating the trajectory of a ball or rocket, is modeled using quadratic equations.
- Engineering: Designing bridges, roads, and other structures often involves solving quadratic equations to determine optimal dimensions and stability.
- Economics: Analyzing market trends, predicting consumer behavior, and optimizing resource allocation can involve quadratic models.
- Computer Graphics: Creating curves and shapes in computer graphics often relies on quadratic equations and their properties.
- Optimization Problems: Finding maximum or minimum values of functions frequently involves solving quadratic equations.
Frequently Asked Questions (FAQ)
Q: Why are complex numbers important?
A: Complex numbers extend the number system beyond real numbers, allowing us to solve equations that have no real solutions. They have profound applications in various fields, particularly in electrical engineering, quantum mechanics, and signal processing.
Q: Can all quadratic equations be solved using the quadratic formula?
A: Yes, the quadratic formula is a universal method for solving any quadratic equation, regardless of whether it can be easily factored.
Q: What does the discriminant tell us?
A: The discriminant (b² - 4ac) reveals the nature of the roots of a quadratic equation: the number of real roots and whether they are distinct or repeated. A negative discriminant indicates complex conjugate roots.
Q: How can I visualize a quadratic equation with complex roots?
A: While you can't directly visualize complex roots on a standard x-y plane, you can visualize the parabola itself. The parabola will not intersect the x-axis if the roots are complex. The complex roots represent points in the complex plane, a two-dimensional plane where the x-axis represents the real part and the y-axis represents the imaginary part of a complex number.
Q: Is there a graphical method to solve quadratic equations?
A: Yes, you can graphically solve quadratic equations by plotting the parabola and finding the x-intercepts (points where the parabola crosses the x-axis). These x-intercepts represent the real roots of the equation. If the parabola doesn't intersect the x-axis, the roots are complex.
Conclusion: Beyond the Numbers
Solving the seemingly simple equation x² + 6x + 25 = 0 opens doors to a deeper understanding of quadratic equations, complex numbers, and their wide-ranging applications. While the initial solution might seem straightforward, the underlying mathematical principles are far-reaching and essential for various scientific and engineering endeavors. The journey from a simple algebraic expression to the exploration of complex numbers and their graphical representation highlights the interconnectedness of mathematical concepts and their power to explain and model the world around us. This equation serves as a microcosm of the beauty and complexity inherent in mathematics. It encourages further exploration and a deeper appreciation for the elegance and practicality of mathematical tools.
Latest Posts
Latest Posts
-
Units For Coefficient Of Friction
Sep 15, 2025
-
Root Mean Square Vs Average
Sep 15, 2025
-
Rust Physical Or Chemical Change
Sep 15, 2025
-
Electron Has A Negative Charge
Sep 15, 2025
-
11 P In A Ft
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 6x 25 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.