X 2 5x 36 0
thesills
Sep 18, 2025 · 6 min read
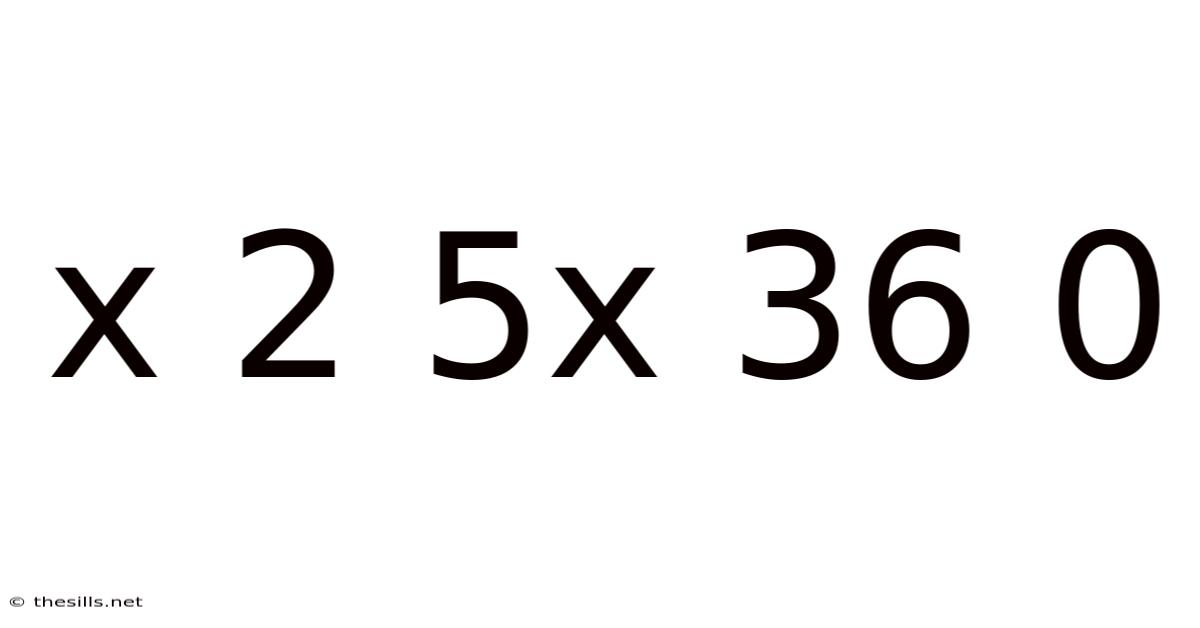
Table of Contents
Decoding the Sequence: x 2 5x 36 0 – A Deep Dive into Pattern Recognition and Mathematical Problem Solving
This article explores the intriguing mathematical sequence "x 2 5x 36 0," delving into the process of identifying patterns, formulating potential solutions, and understanding the underlying mathematical principles involved. We'll unravel the mystery behind this sequence, examining different approaches to solving it and highlighting the importance of logical reasoning and critical thinking in mathematics. This problem is a great example of how seemingly simple sequences can lead to complex and rewarding investigations, enhancing our problem-solving skills.
Introduction: The Allure of Pattern Recognition
Mathematics is often described as the language of the universe. A significant part of this language lies in recognizing and understanding patterns. Sequences like "x 2 5x 36 0" present a fascinating challenge – a puzzle that requires us to decipher the hidden rules and relationships between the numbers. Understanding sequences not only sharpens our analytical skills but also provides a foundation for understanding more advanced mathematical concepts. The seemingly simple nature of this sequence belies its potential complexity, prompting us to investigate various approaches and deepen our understanding of mathematical problem-solving techniques. This investigation will involve exploring the concepts of algebra, equation solving, and logical deduction.
Understanding the Components: Variables and Constants
Before we begin our investigation, let's break down the components of the sequence: "x 2 5x 36 0." We immediately notice the presence of a variable, 'x,' indicating that the sequence is not a simple arithmetic or geometric progression. The other elements – 2, 5x, 36, and 0 – are constants, meaning their values remain unchanged. The presence of 'x' suggests that we are dealing with an algebraic expression, possibly an equation that needs to be solved. This introduces an element of uncertainty, making the problem more stimulating and challenging.
Approach 1: Considering it as a Polynomial Equation
One approach to tackling this sequence is to treat it as a polynomial equation. Considering the presence of x and 5x, we can hypothesize that the sequence represents parts of a polynomial expression set equal to zero. The most straightforward assumption is that it's a quadratic equation of the form ax² + bx + c = 0, where a, b, and c are constants.
Let's try to fit the given sequence into this framework:
- Coefficient of x²: We don't explicitly see an x² term, suggesting that the coefficient 'a' might be zero or that we are missing a part of the equation.
- Coefficient of x: The coefficient of x appears to be 5. This aligns with the term '5x' in the sequence.
- Constant Term: The constant terms are 2, 36, and 0. The presence of multiple constant terms suggests that our initial assumption might be too simplistic. We may need to consider a more complex relationship or a system of equations.
This approach reveals that simply treating the sequence as a single quadratic equation may be insufficient.
Approach 2: Exploring Different Mathematical Operations
Another approach involves considering different mathematical operations that could link the terms. The sequence doesn't immediately suggest an obvious arithmetic or geometric progression. However, let's explore some possibilities:
- Addition/Subtraction: The differences between consecutive terms are not constant, eliminating a simple arithmetic sequence.
- Multiplication/Division: There's no immediate pattern visible through multiplication or division.
- Exponentiation: Exponentiation also doesn't seem to directly relate the terms.
This suggests a more complex underlying structure. We might need to consider combinations of different operations or look for hidden relationships between the terms.
Approach 3: Considering it as a System of Equations
The presence of multiple constant terms (2, 36, and 0) and a variable (x) hints towards a system of equations rather than a single equation. Let's explore potential relationships:
- Equation 1: One possibility is to consider a pair of equations. For example, we might have one equation relating x and 2, and another equation relating x to 36. The '0' could then represent the result of combining these equations in a certain way (e.g., subtraction or addition).
- Equation 2: A possible equation involving x and 2 could be something like x + 2 = y (where y is another variable). Another equation could be related to 5x and 36, perhaps 5x - 36 = z (where z is a different variable). The '0' may represent a condition that must hold true, for example, y - z = 0 or y + z = 0, creating a system of equations to solve.
This approach, while requiring further elaboration to find specific solvable equations, demonstrates a more promising path to a solution.
Approach 4: The Role of Context and Additional Information
It’s crucial to consider that the sequence "x 2 5x 36 0" lacks context. Without knowing the origin or intended application of this sequence, solving it becomes a matter of exploration and hypothesis formation. Additional information, such as the source of the sequence or instructions about what operation should be performed on the terms, would significantly aid in finding a definitive solution.
For instance, if the sequence were part of a larger problem or equation, the relationships between the terms would be clearer. If we were told that this sequence represents steps in a specific algorithm or process, it could help to decipher the rules governing the progression.
Mathematical Principles Involved
This problem highlights several crucial mathematical principles:
- Pattern Recognition: The ability to identify patterns and relationships is fundamental to mathematical problem-solving.
- Algebraic Manipulation: The use of variables and algebraic expressions allows us to represent unknown quantities and formulate equations.
- Equation Solving: Techniques for solving equations, including quadratic equations and systems of equations, are essential for finding solutions.
- Logical Reasoning: Deductive reasoning and logical thinking are vital for formulating hypotheses and testing different approaches.
- Critical Thinking: The ability to evaluate different approaches, identify potential pitfalls, and refine strategies is critical for mathematical success.
FAQ: Addressing Common Questions
Q: Is there a single definitive solution to this sequence?
A: Without additional context or information, there isn't a single definitive solution. Multiple interpretations and approaches are possible, leading to different potential solutions.
Q: How can I improve my ability to solve such mathematical puzzles?
A: Practice is key. Regularly engaging with mathematical problems, focusing on different problem-solving strategies, and exploring diverse mathematical concepts will improve your problem-solving skills.
Q: What if the sequence were different, say, "x 3 7x 24 0"?
A: The approach would be similar – examining possible polynomial equations, exploring various mathematical operations, and considering systems of equations. The specific numbers would influence the equations formulated and the potential solutions.
Conclusion: The Power of Mathematical Exploration
The sequence "x 2 5x 36 0" serves as an excellent example of how a seemingly simple mathematical puzzle can lead to a deep exploration of mathematical principles and problem-solving techniques. While we haven't found a single definitive solution without further context, the process of exploring different approaches has highlighted the importance of pattern recognition, algebraic manipulation, and logical reasoning. The journey of attempting to solve this sequence underscores the power of mathematical exploration and the rewards of critical thinking in mathematical problem-solving. The problem emphasizes that mathematics is not just about finding answers, but also about the process of inquiry, hypothesis formation, and the development of problem-solving skills that are applicable far beyond the realm of pure mathematics. The exercise reminds us that the beauty of mathematics often lies in the journey itself, even more so than in reaching a definitive answer.
Latest Posts
Latest Posts
-
Hydrogen Is Soluble In Water
Sep 18, 2025
-
Are Metals Anions Or Cations
Sep 18, 2025
-
Algae Is Autotroph Or Heterotroph
Sep 18, 2025
-
The Process Of Photosynthesis Converts
Sep 18, 2025
-
Standard Enthalpy Of Formation Fe2o3
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 36 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.