X 2 2x 48 Factor
thesills
Sep 13, 2025 · 5 min read
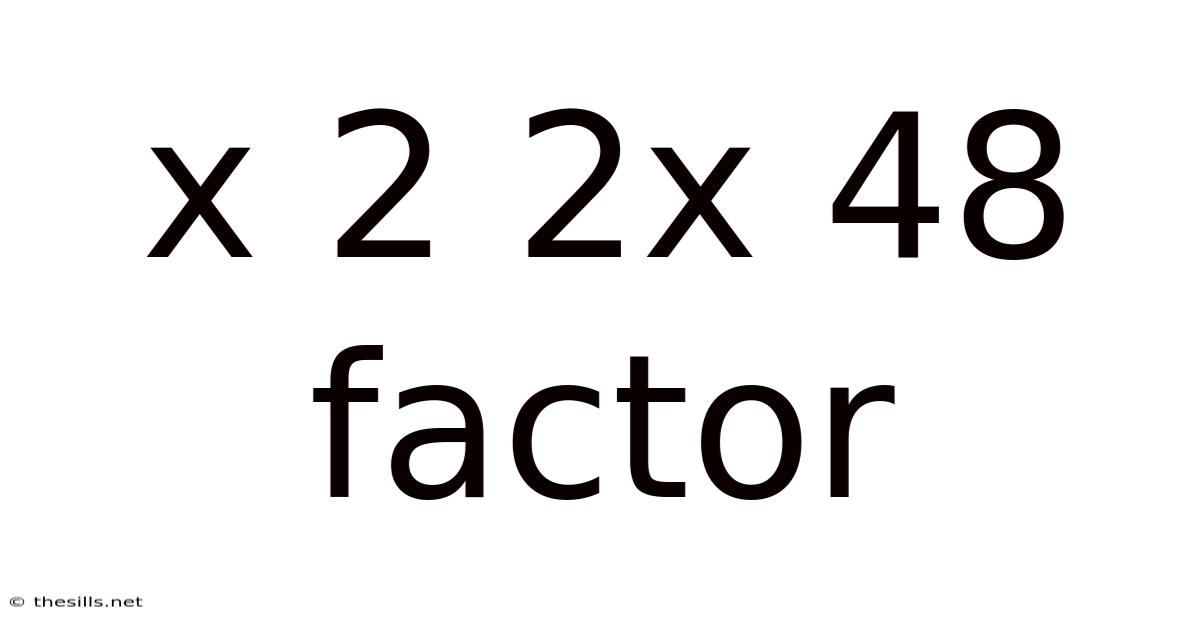
Table of Contents
Decoding the Mystery: Understanding the Factors of x² + 2x - 48
Finding the factors of a quadratic expression like x² + 2x - 48 might seem daunting at first, especially if you're just starting your algebra journey. But fear not! This seemingly complex task can be broken down into manageable steps, revealing a fascinating interplay of numbers and algebra. This article will guide you through the process, explaining not just how to factor this expression, but also why the method works, equipping you with the knowledge to tackle similar problems with confidence.
Understanding Quadratic Expressions
Before diving into the factorization, let's quickly recap what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. Our expression, x² + 2x - 48, fits this form perfectly, with a = 1, b = 2, and c = -48.
The Factoring Process: A Step-by-Step Guide
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions (usually binomials). Here's how we can factor x² + 2x - 48:
Step 1: Identify the coefficients. As mentioned earlier, in our expression x² + 2x - 48, a = 1, b = 2, and c = -48.
Step 2: Find two numbers that add up to 'b' and multiply to 'ac'. This is the crucial step. We need to find two numbers that:
- Add up to 'b' (which is 2).
- Multiply to 'ac' (which is 1 * -48 = -48).
Let's brainstorm pairs of numbers that multiply to -48:
- 1 and -48
- 2 and -24
- 3 and -16
- 4 and -12
- 6 and -8
- 8 and -6
- 12 and -4
- 16 and -3
- 24 and -2
- 48 and -1
Now, let's check which pair adds up to 2: The pair 8 and -6 satisfies both conditions. 8 + (-6) = 2, and 8 * (-6) = -48.
Step 3: Rewrite the expression using the two numbers. We replace the middle term (2x) with the two numbers we found:
x² + 8x - 6x - 48
Step 4: Factor by grouping. We group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x(x + 8) - 6(x + 8)
Notice that (x + 8) is a common factor in both terms.
Step 5: Factor out the common binomial. We factor out (x + 8):
(x + 8)(x - 6)
And there we have it! The factored form of x² + 2x - 48 is (x + 8)(x - 6).
Verifying the Factors: Expanding the Expression
To ensure our factorization is correct, we can expand the factored expression (x + 8)(x - 6) using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * -6 = -6x
- Inner: 8 * x = 8x
- Last: 8 * -6 = -48
Combining these terms, we get x² - 6x + 8x - 48, which simplifies to x² + 2x - 48 – our original expression. This confirms that our factorization is accurate.
The Significance of Factoring
Factoring quadratic expressions is a fundamental skill in algebra with wide-ranging applications. It's essential for:
- Solving quadratic equations: By setting the factored expression equal to zero, we can easily find the roots (solutions) of the quadratic equation. In our case, setting (x + 8)(x - 6) = 0 gives us x = -8 and x = 6 as solutions.
- Simplifying algebraic expressions: Factoring can simplify complex expressions, making them easier to manipulate and understand.
- Graphing quadratic functions: The factored form reveals the x-intercepts (where the graph crosses the x-axis) of the corresponding parabola. In our example, the x-intercepts are -8 and 6.
- Solving real-world problems: Quadratic equations model many real-world phenomena, from projectile motion to the area of shapes. Factoring helps us solve these problems efficiently.
A Deeper Dive into the Mathematics: Why Does This Method Work?
The method we used relies on the distributive property of multiplication. The distributive property states that a(b + c) = ab + ac. By reversing this process, we're essentially "undoing" the multiplication that created the quadratic expression.
Consider the general form of a factored quadratic: (x + p)(x + q). Expanding this gives:
x² + qx + px + pq = x² + (p + q)x + pq
Comparing this to the standard form ax² + bx + c, we see that:
- b = p + q
- c = pq
This explains why we look for two numbers that add up to 'b' and multiply to 'c' (or 'ac' when a ≠ 1). We're essentially finding the values of 'p' and 'q' that satisfy these conditions.
Addressing Common Challenges and FAQs
Q1: What if I can't find two numbers that add up to 'b' and multiply to 'ac'?
A1: If you can't find such numbers, it means the quadratic expression is likely prime – it cannot be factored using integers. You might need to use the quadratic formula to find the roots, or you might need to factor out a greatest common factor (GCF) if one exists.
Q2: What if 'a' is not equal to 1?
A2: If a ≠ 1, the process becomes slightly more complex. You can use the AC method, which involves multiplying 'a' and 'c', finding two numbers that add up to 'b' and multiply to 'ac', and then factoring by grouping. Alternatively, you can utilize techniques such as completing the square or the quadratic formula.
Q3: Are there other methods to factor quadratic expressions?
A3: Yes, there are alternative methods, including completing the square and the quadratic formula. The quadratic formula is particularly useful when factoring is difficult or impossible. Completing the square provides insight into the structure of parabolas.
Conclusion: Mastering the Art of Factoring
Factoring quadratic expressions, like x² + 2x - 48, might seem challenging initially, but with practice and a clear understanding of the underlying principles, it becomes a straightforward and powerful tool. This process, while seemingly focused on manipulating symbols, unveils a deeper understanding of the relationships between numbers and algebra. By mastering factoring, you gain access to a wider range of problem-solving techniques in mathematics and beyond. Remember the steps, practice regularly, and soon you’ll be factoring quadratic expressions with ease and confidence! Embrace the challenge, and enjoy the rewarding journey of unlocking the secrets hidden within these algebraic expressions.
Latest Posts
Latest Posts
-
1 Horse Power To Kw
Sep 13, 2025
-
High Accuracy And Low Precision
Sep 13, 2025
-
Fructose Is An Example Of
Sep 13, 2025
-
X 4 2x 2 1
Sep 13, 2025
-
Is Co2 A Covalent Compound
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 48 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.