X 2 14x 33 0
thesills
Sep 15, 2025 · 7 min read
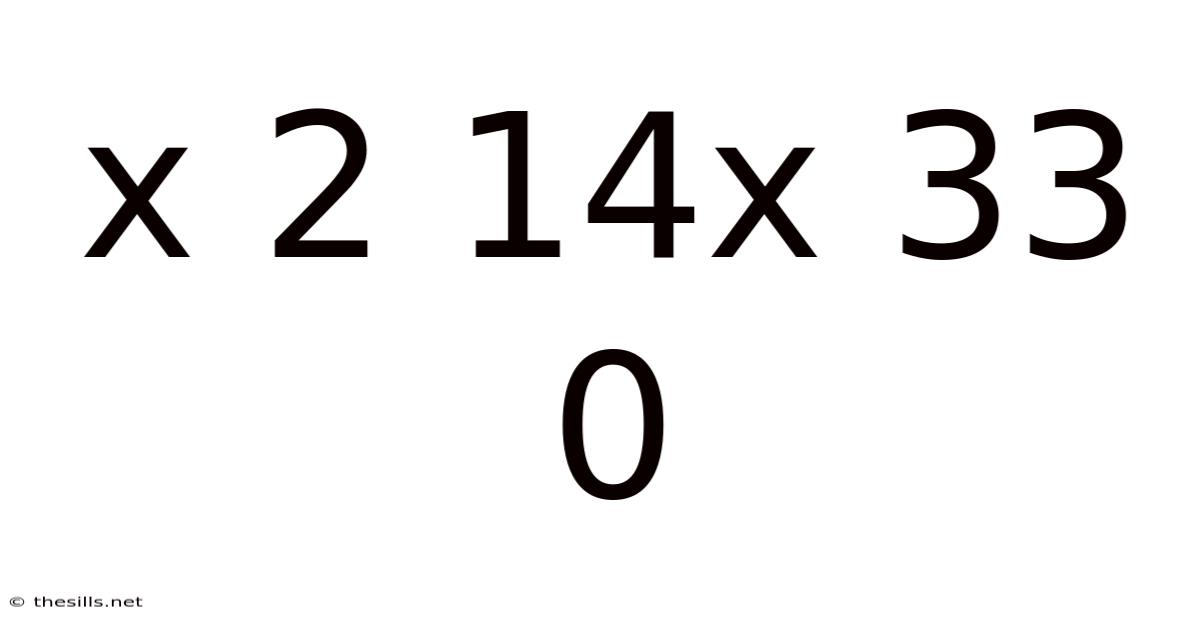
Table of Contents
Decoding the Sequence: x 2 14x 33 0 – A Deep Dive into Mathematical Patterns and Problem Solving
This article explores the seemingly cryptic sequence "x 2 14x 33 0," analyzing potential patterns, underlying mathematical principles, and various approaches to decipher its meaning. We will delve into different interpretations, considering possibilities ranging from simple arithmetic progressions to more complex algebraic expressions, and even explore potential connections to number theory or coding. This investigation will not only unravel the mystery of this specific sequence but also provide valuable insights into problem-solving strategies and mathematical thinking.
Understanding the Problem: What We Know and What We Don't
The sequence "x 2 14x 33 0" presents a unique challenge. The presence of "x" immediately suggests an algebraic equation or expression, rather than a purely arithmetic sequence. The numbers 2, 14, 33, and 0 are seemingly unrelated at first glance, making it difficult to immediately identify a clear pattern. Our primary goal is to determine the value(s) of "x" that would satisfy the sequence, or if the sequence represents a different mathematical concept altogether. We don't know the underlying rules or the intended context, making this a problem requiring creative and systematic investigation.
Approach 1: Exploring Simple Arithmetic Progressions
A basic approach would be to check for simple arithmetic progressions. However, a quick inspection reveals that the differences between consecutive numbers (2-14, 14-33, 33-0) are irregular (-12, 19, -33). This eliminates the possibility of a simple arithmetic or even a geometric progression. This negative result, however, points us in a more complex direction.
Approach 2: Investigating Algebraic Equations
Given the presence of "x," we should consider algebraic equations. Several possibilities arise, depending on how the "x" is incorporated into the sequence. Let's explore some scenarios:
-
Scenario 1: x as a constant: If "x" represents a constant value, we could try fitting the numbers into a polynomial equation. A simple quadratic equation might be a starting point. However, this approach quickly becomes complex and requires sophisticated methods like least squares regression to fit the data, which doesn't yield an easily interpretable solution.
-
Scenario 2: x as a variable in an equation: A more fruitful approach might involve exploring the possibility that the sequence represents parts of an equation. Perhaps the sequence represents terms in an equation where 'x' is the unknown variable. We might attempt to form an equation using these numbers and solve for x. This requires creative manipulation and a careful examination of possible relationships. Let's consider some potential equations:
-
Possibility A: We could hypothesize that the sequence represents coefficients of a polynomial: ax³ + bx² + cx + d = 0. In this case, we could have a = x, b = 2, c = 14x, and d = 33. Solving for x in a cubic equation of this nature would require advanced algebraic techniques, possibly even numerical methods to find approximate solutions.
-
Possibility B: A different interpretation might involve a sequence of operations. For instance, we could consider the sequence as a series of steps where x is involved in each step:
- Step 1: x
- Step 2: 2
- Step 3: 14x
- Step 4: 33
- Step 5: 0
This implies that there might be a hidden operator or rule relating each term. However, without further information or context, the possibilities are vast and difficult to isolate.
-
Approach 3: Exploring Number Theory and Other Mathematical Concepts
Beyond basic algebra, we could explore connections to number theory. Perhaps the numbers hold some special relationship based on their prime factorization, divisibility, or other number-theoretic properties. This line of inquiry could be especially relevant if the sequence were part of a larger, more complex mathematical problem.
Similarly, we could look into other mathematical concepts such as:
- Combinatorics: Is the sequence related to combinations, permutations, or other combinatorial structures?
- Sequences and Series: Could the sequence be part of a known sequence or series, perhaps with a modified or generalized rule?
- Modular Arithmetic: Are there patterns emerging when considering the remainders after dividing by a certain modulus?
However, without additional information about the origin or context of the sequence, pursuing these avenues might be unproductive unless more clues are provided.
Approach 4: Considering Context and Potential Errors
A critical consideration is the context in which the sequence "x 2 14x 33 0" appeared. Without knowing the source – whether it's a math puzzle, a coding problem, a fragment of a larger equation, or something else entirely – our attempts to decode it are hampered.
There's also the possibility of errors or misinterpretations. Is the sequence accurately transcribed? Could there be missing elements or symbols that would clarify its meaning? Careful review of the source material is crucial in ruling out simple mistakes.
Step-by-Step Problem Solving Strategy
To effectively solve such problems, a systematic approach is vital:
-
Clearly define the problem: What exactly are we trying to achieve? What information do we have, and what are we missing? In this case, we are trying to understand the meaning and potential solutions related to the sequence "x 2 14x 33 0".
-
Explore basic approaches: Start with simple methods. Check for arithmetic or geometric progressions, look for obvious patterns.
-
Introduce more advanced techniques: If simple approaches fail, consider algebra, number theory, or other mathematical concepts. Formulate hypotheses and test them rigorously.
-
Consider alternative interpretations: The sequence may represent something other than a simple mathematical progression. Think creatively and explore multiple possibilities.
-
Systematic testing and evaluation: Test each hypothesis systematically. Use mathematical tools and software where needed.
-
Documentation and review: Keep a record of your work, including your hypotheses, calculations, and results. Regularly review your work to ensure accuracy and identify potential errors.
-
Seek clarification or additional information: If you're stuck, consider seeking additional information or clarification from the source of the problem.
Frequently Asked Questions (FAQs)
Q1: Is there a single, definitive solution to this sequence?
A1: Without additional context or information, there is no single, definitive solution. The presence of "x" introduces multiple possibilities, and the numbers themselves don't immediately reveal a clear pattern using elementary arithmetic or geometric progressions. More information is needed.
Q2: What kind of mathematical knowledge is required to solve this?
A2: Solving this problem requires a foundation in algebra, potentially extending to more advanced areas like polynomial equations, numerical methods, and possibly number theory. Problem-solving skills and creative thinking are equally important.
Q3: Could this sequence be part of a larger problem?
A3: Absolutely. It's quite likely that this sequence is just a fragment of a larger mathematical problem, puzzle, or code. The context is crucial in determining its true meaning.
Q4: What if the sequence contains errors?
A4: If the sequence contains errors, it makes the problem even more challenging. We would need to try to identify and correct potential errors based on the context and any available additional information.
Conclusion: The Importance of Context and Creative Problem Solving
The seemingly simple sequence "x 2 14x 33 0" presents a fascinating challenge that highlights the importance of context, systematic thinking, and creative problem-solving in mathematics. While we haven't arrived at a definitive answer without further information, the process of investigating different approaches and mathematical concepts has revealed valuable insights into various mathematical techniques. The exploration underscores the fact that even seemingly simple problems can reveal surprising complexity and necessitate the application of diverse mathematical tools and creative thinking. This kind of problem-solving exercise is crucial in fostering a deeper understanding of mathematical concepts and building critical thinking skills. Future explorations might incorporate advanced numerical analysis, iterative methods, or even machine learning algorithms if sufficient data or context were available. The journey of deciphering this sequence is itself a testament to the beauty and complexity of mathematics.
Latest Posts
Latest Posts
-
Which Description Best Defines Health
Sep 16, 2025
-
Patricks House Is A Turtle
Sep 16, 2025
-
Chemical Formula Of Zinc Hydroxide
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 14x 33 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.