Whats 30 Percent Of 90
thesills
Sep 17, 2025 · 5 min read
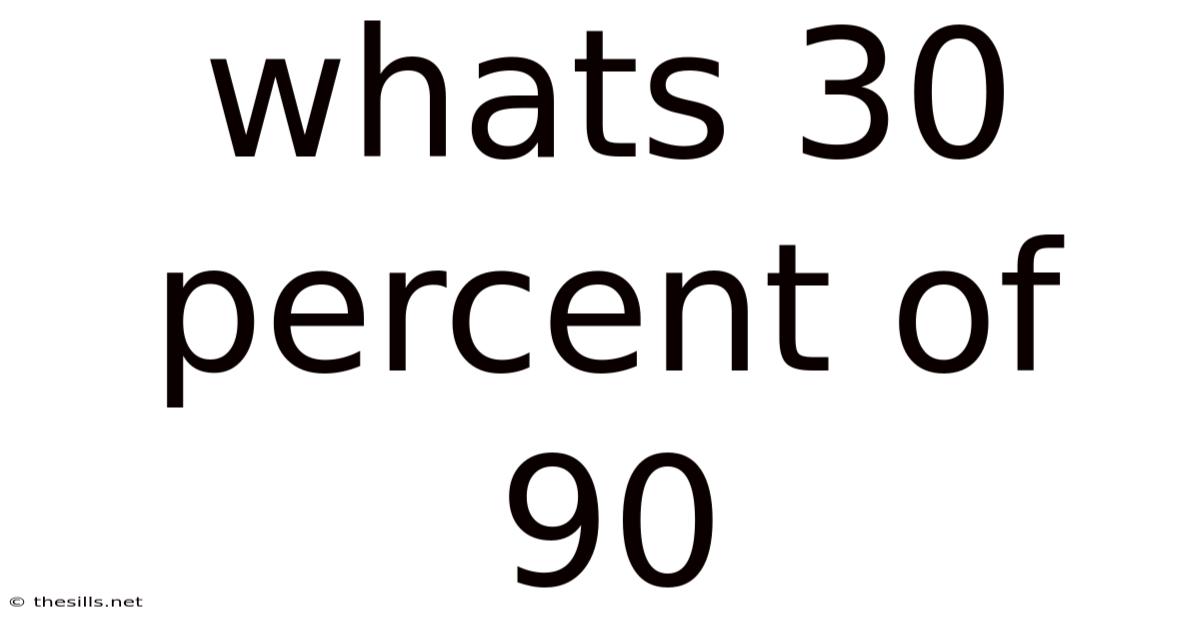
Table of Contents
What's 30 Percent of 90? A Deep Dive into Percentages and Their Applications
Finding 30 percent of 90 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying principles of percentages and their widespread applications is far more valuable. This article will not only provide the answer to this specific question but also delve into the fundamental concepts of percentages, exploring different methods of calculation, real-world examples, and practical applications across various fields.
Understanding Percentages: A Foundation for Calculation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 30% signifies 30 out of 100, or 30/100, which simplifies to 3/10 as a fraction and 0.3 as a decimal. This fundamental understanding is crucial for solving percentage problems.
Method 1: The Direct Calculation Method
The most straightforward way to calculate 30% of 90 is to convert the percentage to a decimal and multiply it by the number.
-
Step 1: Convert the percentage to a decimal: 30% = 30/100 = 0.3
-
Step 2: Multiply the decimal by the number: 0.3 * 90 = 27
Therefore, 30% of 90 is 27.
Method 2: The Fraction Method
Alternatively, you can use the fraction equivalent of 30%.
-
Step 1: Express the percentage as a fraction: 30% = 30/100
-
Step 2: Simplify the fraction: 30/100 simplifies to 3/10
-
Step 3: Multiply the fraction by the number: (3/10) * 90 = 270/10 = 27
Again, the answer is 27. This method highlights the relationship between percentages, fractions, and decimals, reinforcing the fundamental concepts.
Method 3: Using Proportions
A proportion establishes a relationship between two ratios. We can set up a proportion to solve this problem:
-
Step 1: Set up the proportion: x/90 = 30/100 (where x represents 30% of 90)
-
Step 2: Cross-multiply: 100x = 90 * 30
-
Step 3: Solve for x: 100x = 2700 => x = 2700/100 = 27
This method demonstrates the proportional relationship between the percentage and the whole number, providing a different perspective on the calculation.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Stores often advertise discounts as percentages. For instance, a 30% discount on a $90 item means you save 27 dollars, paying only $63.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the total amount. Calculating the tax amount requires understanding percentage calculations.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are usually expressed as annual percentages. Calculating the interest earned or paid depends on accurate percentage calculations.
-
Financial Statements: Financial reports use percentages extensively to represent various financial ratios, such as profit margins, debt-to-equity ratios, and return on investment (ROI). Analyzing these reports requires a strong understanding of percentages.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. For example, expressing survey results or the success rate of a treatment as percentages improves clarity and understanding.
-
Scientific Calculations: Percentages are commonly used in scientific research to represent changes in quantities, concentrations, or experimental results. Understanding percentages is crucial for accurate data interpretation and reporting.
Beyond the Basics: Advanced Percentage Problems
While finding 30% of 90 is a relatively simple calculation, percentage problems can become significantly more complex. Consider these advanced scenarios:
-
Finding the original value: If you know a certain percentage of a number and the resulting value, you can work backward to find the original number. For example, if 30% of a number is 27, what is the original number? This involves using inverse operations.
-
Calculating percentage increase or decrease: Determining the percentage change between two values is crucial for analyzing trends and growth. For example, what is the percentage increase from 90 to 120?
-
Compounding percentages: When dealing with multiple percentage changes applied sequentially, the calculations become more involved. Compound interest, for example, involves applying interest to the principal amount plus accumulated interest over time.
Frequently Asked Questions (FAQ)
-
Q: What is the formula for calculating percentages?
- A: The basic formula is: (Percentage/100) * Number = Result
-
Q: How do I calculate a percentage increase?
- A: [(New Value - Old Value) / Old Value] * 100 = Percentage Increase
-
Q: How do I calculate a percentage decrease?
- A: [(Old Value - New Value) / Old Value] * 100 = Percentage Decrease
-
Q: What if I need to calculate more than one percentage of a number sequentially?
- A: You must calculate each percentage one after the other, applying the result of the first calculation to the next. For example, if you need to find 10% of a number and then 20% of the result, you'd first calculate 10%, and then calculate 20% of that new number.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 30% of 90—which equals 27—is a fundamental step in understanding percentages. However, the true value lies in grasping the broader concepts and applications of this essential mathematical tool. From everyday transactions to complex financial analyses and scientific research, proficiency in percentage calculations is an invaluable skill that empowers individuals to navigate various aspects of life more effectively. By understanding the different methods of calculation and their applications, you equip yourself with a powerful tool for problem-solving and informed decision-making. Mastering percentages is not merely about arithmetic; it's about acquiring a crucial skill set for personal and professional success.
Latest Posts
Latest Posts
-
Hibiscus Parts Of The Flower
Sep 17, 2025
-
Synopsis Of The Happy Prince
Sep 17, 2025
-
Rotational Symmetry For Isosceles Triangle
Sep 17, 2025
-
When Are Recessive Alleles Expressed
Sep 17, 2025
-
22 7 As A Decimal
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.