What Is 70 Of $20
thesills
Sep 16, 2025 · 5 min read
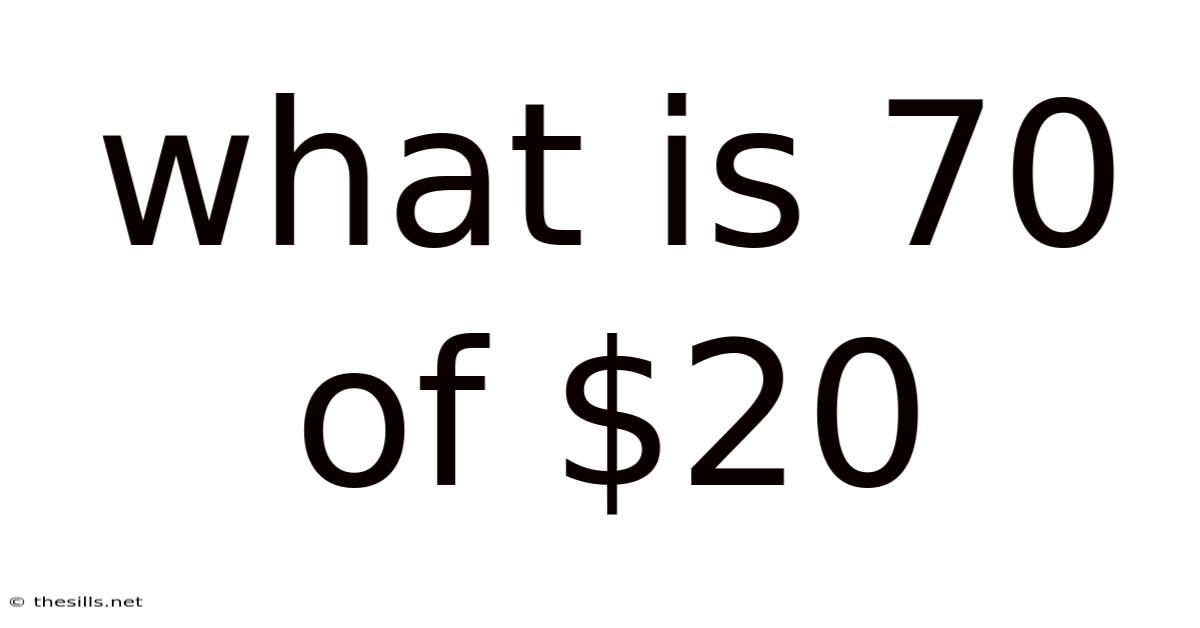
Table of Contents
What is 70% of $20? A Deep Dive into Percentages and Their Applications
Finding 70% of $20 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from budgeting and finance to understanding statistics and data analysis. This article will not only answer the question directly but also explore the concept of percentages in detail, providing you with the tools to tackle similar problems independently. We'll cover different calculation methods, real-world applications, and frequently asked questions. This comprehensive guide aims to equip you with a solid understanding of percentages and their practical implications.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." When we say 70%, we mean 70 out of 100, or 70/100, which simplifies to 7/10. This fractional representation is key to understanding how percentage calculations work.
Calculating 70% of $20: Three Methods
There are several ways to calculate 70% of $20. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. To find 70% of a number, we first convert the percentage to its decimal equivalent by dividing it by 100. 70% divided by 100 is 0.70 (or simply 0.7). Then, we multiply this decimal by the number we're interested in:
70% of $20 = 0.70 * $20 = $14
Method 2: Using Fractions
As we established earlier, 70% is equivalent to the fraction 7/10. We can use this fraction to calculate 70% of $20:
7/10 * $20 = ($7 * $20) / 10 = $140 / 10 = $14
This method is particularly useful when the percentage can be easily expressed as a simple fraction.
Method 3: Proportions
This method uses the concept of ratios and proportions. We can set up a proportion to solve for the unknown value:
70/100 = x/$20
To solve for x (70% of $20), we cross-multiply:
70 * $20 = 100 * x
1400 = 100x
x = 1400 / 100 = $14
This method is useful for understanding the underlying relationship between percentages and proportions.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in many real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, tips, and profit margins all involve percentages. For instance, if a store offers a 70% discount on an item, knowing how to calculate that discount is crucial.
-
Statistics and Data Analysis: Percentages are used extensively to represent data in graphs, charts, and reports. For example, understanding the percentage of people who prefer a certain product helps businesses make informed decisions.
-
Everyday Life: Calculating sale prices, understanding nutritional information (e.g., percentage of daily value), and even figuring out the percentage of a task you’ve completed all involve percentage calculations.
-
Science: Percentages are used to express concentrations, yields, and error rates in scientific experiments and research.
Beyond the Basics: More Complex Percentage Problems
While calculating 70% of $20 is relatively simple, many real-world problems involve more complex calculations. Let's explore a few examples:
- Finding the Original Price: If an item is discounted by 30% and the sale price is $14, what was the original price? This requires working backwards from the sale price using the concept of percentages. We know that the sale price represents 70% (100% - 30%) of the original price.
Let's set up the equation: 0.7x = $14, where x is the original price. Solving for x, we get x = $14 / 0.7 = $20. Therefore, the original price was $20.
- Calculating Percentage Increase or Decrease: If a quantity increases from 20 to 28, what is the percentage increase? First, we find the difference (28 - 20 = 8). Then, we divide the difference by the original value (8/20 = 0.4) and multiply by 100% to express it as a percentage (0.4 * 100% = 40%). Therefore, the quantity increased by 40%.
Frequently Asked Questions (FAQ)
-
What if the percentage is not a whole number? You can use the same methods (decimal, fraction, or proportion) with decimal percentages. For example, to find 72.5% of $20, you would use 0.725 * $20.
-
How can I calculate percentages quickly without a calculator? For simple percentages like 10%, 20%, 50%, etc., you can use mental math techniques. For instance, 10% of $20 is $2, so 20% is $4, and 50% is $10. You can combine these to calculate other percentages.
-
Are there any online calculators for percentages? Yes, many websites offer free online percentage calculators. These tools can be helpful for quick calculations or for checking your work. However, understanding the underlying principles is crucial for broader application.
-
What if I need to calculate percentage change over multiple periods? For multiple period percentage changes, you need to calculate the percentage change for each period sequentially, not simply add or average the individual changes. This is because percentage changes are relative to the base value, which changes after each period.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 70% of $20, as we've seen, is a straightforward process that yields an answer of $14. However, the real value lies in understanding the broader principles of percentages and their wide-ranging applications. From managing personal finances to interpreting complex data, the ability to work comfortably with percentages is a valuable skill that enhances your understanding of the world around you. By mastering these techniques, you equip yourself not only to solve specific problems but also to approach new challenges with confidence and competence. This article has provided a foundation for understanding percentages and their practical use. Continued practice and exploration of more complex problems will solidify your understanding and make you proficient in this essential mathematical concept. Remember, the key is not just getting the right answer, but understanding why that answer is correct.
Latest Posts
Latest Posts
-
Which Statement Best Describes Electrons
Sep 16, 2025
-
How Tall Is 168 Centimeters
Sep 16, 2025
-
How Many Atoms In Gold
Sep 16, 2025
-
Magnetic Moment Of A Proton
Sep 16, 2025
-
Why Is Acetone So Cold
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of $20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.