What Is 30 Of 9
thesills
Sep 12, 2025 · 5 min read
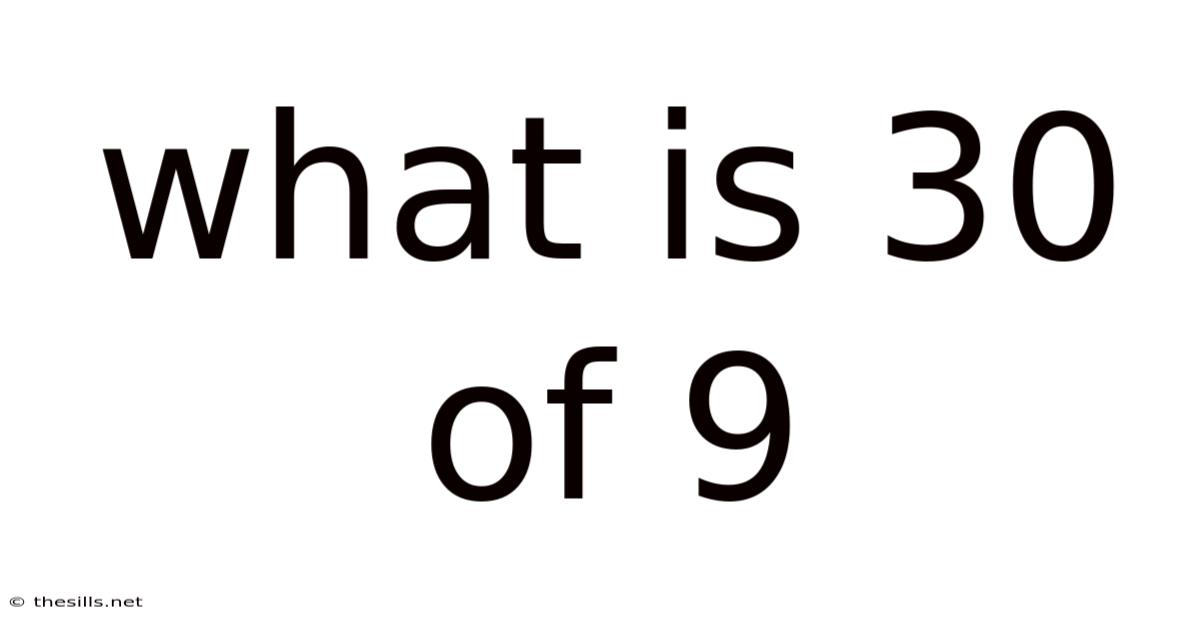
Table of Contents
What is 30% of 9? A Comprehensive Guide to Percentages and their Applications
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts in a store to analyzing financial reports. This article will comprehensively explore how to calculate 30% of 9, explaining the underlying principles and providing practical examples to solidify your understanding. We'll delve into different methods, explore the broader concept of percentages, and answer frequently asked questions. This guide is designed for learners of all levels, from those just beginning to grasp percentage concepts to those looking to refine their mathematical skills.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". Therefore, 30% means 30 out of 100, which can also be written as the fraction 30/100 or the decimal 0.30. This fundamental understanding is crucial for calculating percentages effectively.
Method 1: Converting Percentage to Decimal
This is perhaps the most straightforward approach. We convert the percentage to its decimal equivalent and then multiply it by the number.
Steps:
-
Convert the percentage to a decimal: To convert 30% to a decimal, divide it by 100: 30 ÷ 100 = 0.30
-
Multiply the decimal by the number: Multiply the decimal (0.30) by the number you want to find the percentage of (9): 0.30 x 9 = 2.7
Therefore, 30% of 9 is 2.7
Method 2: Using Fractions
This method involves expressing the percentage as a fraction and then performing the calculation.
Steps:
-
Express the percentage as a fraction: 30% can be written as the fraction 30/100.
-
Simplify the fraction (optional): The fraction 30/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10: 30/100 = 3/10
-
Multiply the fraction by the number: Multiply the simplified fraction (3/10) by the number (9): (3/10) x 9 = 27/10
-
Convert the result to a decimal (if necessary): Convert the improper fraction 27/10 to a decimal by dividing the numerator by the denominator: 27 ÷ 10 = 2.7
Therefore, 30% of 9 is 2.7
Method 3: Using Proportions
This method utilizes the concept of proportionality to solve the problem.
Steps:
-
Set up a proportion: We can set up a proportion to represent the problem: 30/100 = x/9, where 'x' represents 30% of 9.
-
Cross-multiply: Cross-multiply the terms in the proportion: 30 x 9 = 100 x
-
Solve for x: Solve for 'x' by dividing both sides of the equation by 100: (30 x 9) / 100 = x => 270 / 100 = x
-
Simplify: Simplify the result to obtain the answer: x = 2.7
Therefore, 30% of 9 is 2.7
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in many real-world scenarios. Here are a few examples:
-
Sales and Discounts: Calculating discounts on items during sales. For example, a 30% discount on a $9 item would mean a saving of $2.70.
-
Taxes: Determining the amount of sales tax or other taxes added to a purchase price.
-
Tips and Gratuities: Calculating tips in restaurants or service charges.
-
Financial Analysis: Analyzing financial statements, calculating profit margins, and understanding growth rates.
-
Statistics and Probability: Percentages are used extensively in statistical analysis and probability calculations to represent proportions and likelihoods.
-
Everyday Life: Numerous everyday situations involve percentages, such as calculating the percentage of ingredients in a recipe, determining the proportion of a task completed, or understanding survey results.
Further Exploration of Percentages: Advanced Concepts
While calculating 30% of 9 is a relatively straightforward calculation, understanding percentages extends far beyond basic computations. Here's a glimpse into some advanced aspects:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
-
Percentage Change: Determining the increase or decrease in a value over time, often expressed as a percentage.
-
Percentage Points: Distinguishing between percentage change and percentage points, which are often confused.
-
Weighted Averages: Calculating averages where different values carry different weights or importance.
-
Statistical Significance: Using percentages to determine if a difference observed in data is statistically meaningful.
Frequently Asked Questions (FAQ)
Q1: What is the easiest method to calculate percentages?
A1: The easiest method often depends on personal preference and the specific problem. Converting the percentage to a decimal and multiplying is usually the most straightforward and widely applicable approach.
Q2: Can I use a calculator to calculate percentages?
A2: Absolutely! Most calculators have a percentage function (%) that simplifies the process. You can directly input the calculation as "30% of 9" or perform the steps manually as described above.
Q3: How do I calculate a percentage increase or decrease?
A3: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For a percentage decrease, follow the same steps, but the result will be negative.
Q4: What if I need to calculate a percentage of a larger number?
A4: The methods described above remain applicable regardless of the size of the number. You would simply substitute the larger number into the calculations.
Q5: Are there any online tools or resources available to help with percentage calculations?
A5: Numerous online calculators and educational resources are available to assist with percentage calculations, offering step-by-step guidance and explanations.
Conclusion
Calculating 30% of 9, resulting in 2.7, is a fundamental percentage calculation. Mastering this simple concept opens the door to a broader understanding of percentages, a vital mathematical tool applicable across diverse fields. By understanding the various methods – using decimals, fractions, or proportions – you can approach percentage problems with confidence and apply this crucial skill to various real-world situations. Remember to practice regularly to reinforce your understanding and develop fluency in percentage calculations. The more you practice, the more effortless and intuitive these calculations will become, empowering you to confidently tackle more complex percentage problems in the future.
Latest Posts
Latest Posts
-
19th Letter Of The Alphabet
Sep 12, 2025
-
Energy Transformation Of A Lamp
Sep 12, 2025
-
Lewis Dot Symbol Of Mg
Sep 12, 2025
-
In The Ellipse Shown Below
Sep 12, 2025
-
Moment Of Inertia For Hoop
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.