What Is 30 Of 36
thesills
Sep 12, 2025 · 5 min read
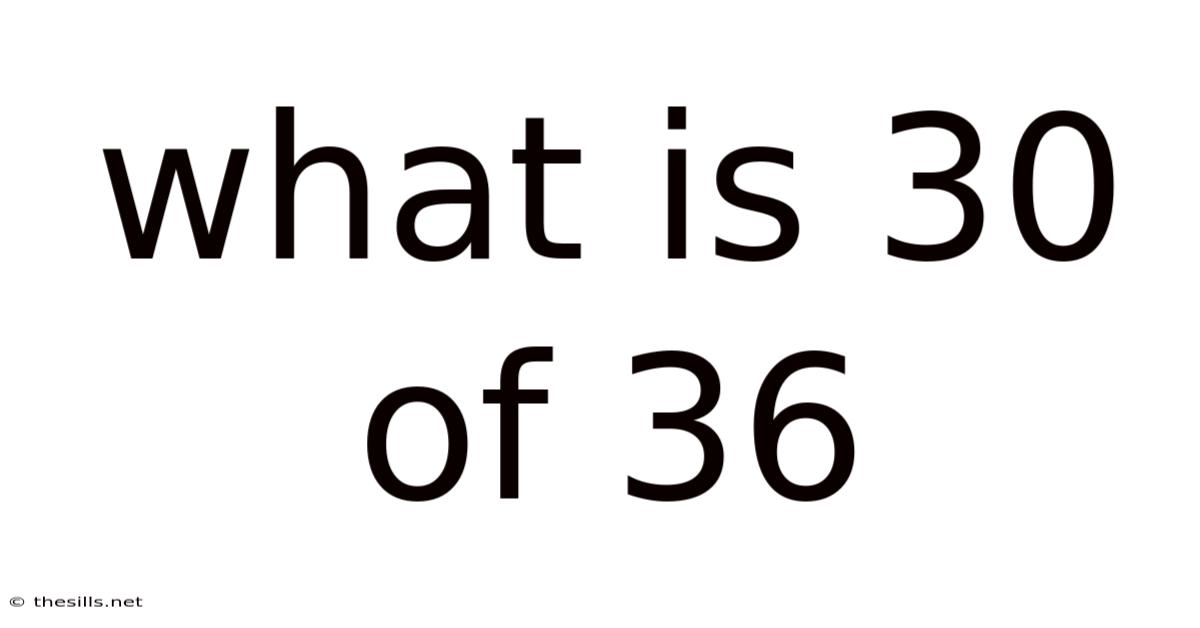
Table of Contents
What is 30 out of 36? Understanding Fractions, Percentages, and Ratios
The question, "What is 30 out of 36?", seemingly simple, opens a door to a world of mathematical concepts crucial for everyday life. Understanding how to solve this problem involves grasping the fundamentals of fractions, percentages, and ratios. This article will not only provide the answer but also delve into the underlying principles, equipping you with the skills to tackle similar problems confidently. We'll explore different methods of calculation, offering clarity and building a strong foundation in mathematical reasoning.
Understanding the Basics: Fractions, Percentages, and Ratios
Before we tackle "30 out of 36," let's clarify the core mathematical concepts involved.
1. Fractions: A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). In our case, "30 out of 36" can be written as the fraction 30/36. The numerator (30) indicates the part, while the denominator (36) represents the whole.
2. Percentages: A percentage is a fraction expressed as a number out of 100. It indicates a proportion relative to a whole. To convert a fraction to a percentage, we divide the numerator by the denominator and multiply by 100.
3. Ratios: A ratio compares two or more quantities. It can be expressed using a colon (e.g., 30:36) or as a fraction (30/36). Ratios show the relative sizes of different parts of a whole.
Calculating 30 out of 36: Step-by-Step Approach
There are several ways to determine what 30 out of 36 represents. Let's explore the most common methods:
Method 1: Simplifying the Fraction
The simplest approach involves simplifying the fraction 30/36 to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it.
The GCD of 30 and 36 is 6. Dividing both the numerator and denominator by 6 gives us:
30 ÷ 6 = 5 36 ÷ 6 = 6
Therefore, 30/36 simplifies to 5/6. This means 30 out of 36 is equivalent to 5 out of 6.
Method 2: Converting to a Percentage
To express 30 out of 36 as a percentage, we follow these steps:
-
Divide the numerator by the denominator: 30 ÷ 36 = 0.8333...
-
Multiply the result by 100: 0.8333... × 100 = 83.33% (approximately)
Therefore, 30 out of 36 is approximately 83.33%.
Method 3: Using Decimal Representation
Dividing the numerator (30) by the denominator (36) directly gives the decimal representation:
30 ÷ 36 = 0.8333...
This decimal, 0.8333..., represents the proportion of 30 out of 36. This is another way to express the result, often useful in contexts requiring numerical precision.
Real-World Applications: Understanding Proportions
Understanding fractions, percentages, and ratios is vital in numerous real-world scenarios. Here are a few examples:
-
Calculating Grades: If you answered 30 questions correctly out of 36 on a test, your score would be approximately 83.33%.
-
Financial Calculations: Imagine you invested $36 and earned a profit of $30. Your return on investment would be 83.33%.
-
Cooking and Baking: Recipes often use ratios. If a recipe calls for a 36:30 ratio of flour to sugar, you can adjust the quantities while maintaining the same proportion.
-
Construction and Engineering: Ratios and proportions are fundamental in construction, ensuring structural integrity and accurate measurements.
Expanding Your Understanding: Further Exploration
While we've answered the initial question, this problem opens doors to more complex mathematical concepts. Let's delve into some of them:
-
Equivalent Fractions: We saw that 30/36 simplifies to 5/6. There are infinitely many equivalent fractions representing the same value, such as 10/12, 15/18, and so on. Understanding equivalent fractions is crucial for comparing and manipulating fractions effectively.
-
Improper Fractions and Mixed Numbers: If the numerator of a fraction is larger than the denominator, it's an improper fraction. For instance, 36/30 is an improper fraction. It can be converted to a mixed number, which comprises a whole number and a proper fraction (e.g., 1 6/30).
-
Working with Decimals: Understanding decimal representation is crucial for various calculations, especially when working with percentages and proportions in financial or scientific contexts. The ability to convert between fractions, decimals, and percentages is invaluable.
-
Proportional Reasoning: This involves using ratios and proportions to solve problems. For example, if you know the ratio of ingredients in a recipe and want to scale it up or down, proportional reasoning is essential.
-
Advanced Ratio Problems: More complex problems might involve multiple ratios or proportions, requiring a more advanced understanding of algebraic concepts.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 30/36?
A: The simplest form of 30/36 is 5/6. This is achieved by dividing both the numerator and denominator by their greatest common divisor, which is 6.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. For example, (30/36) x 100 ≈ 83.33%.
Q: What are some real-world applications of understanding 30 out of 36?
A: Understanding this type of calculation is crucial for various applications, including calculating grades, analyzing financial data, adjusting recipes, and solving problems in construction and engineering where proportions and ratios are involved.
Q: Can you explain the concept of a ratio?
A: A ratio compares two or more quantities. It can be expressed using a colon (e.g., 30:36) or as a fraction (30/36). It shows the relative sizes of different parts of a whole.
Q: What if the numbers were larger or more complex?
A: The principles remain the same. You would still simplify the fraction to its lowest terms by finding the greatest common divisor, or you would divide the numerator by the denominator to convert to a decimal or percentage. Larger numbers might require a calculator for precise calculations.
Conclusion
The seemingly straightforward question, "What is 30 out of 36?", serves as a gateway to understanding fundamental mathematical concepts. By exploring fractions, percentages, ratios, and their real-world applications, we've built a strong foundation for tackling more complex problems. Remember, mastering these concepts is not just about memorizing formulas; it's about developing a deeper understanding of proportions and their significance in various aspects of life. This knowledge empowers you to approach numerical challenges with confidence and solve problems effectively in diverse situations.
Latest Posts
Latest Posts
-
Play To The Gallery Meaning
Sep 12, 2025
-
Is Trees Abiotic Or Biotic
Sep 12, 2025
-
Gravity Between Earth And Sun
Sep 12, 2025
-
Differentiate Between Taxonomy And Systematics
Sep 12, 2025
-
Formula For Efficiency In Physics
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.