What Is 30 Of 250
thesills
Sep 14, 2025 · 5 min read
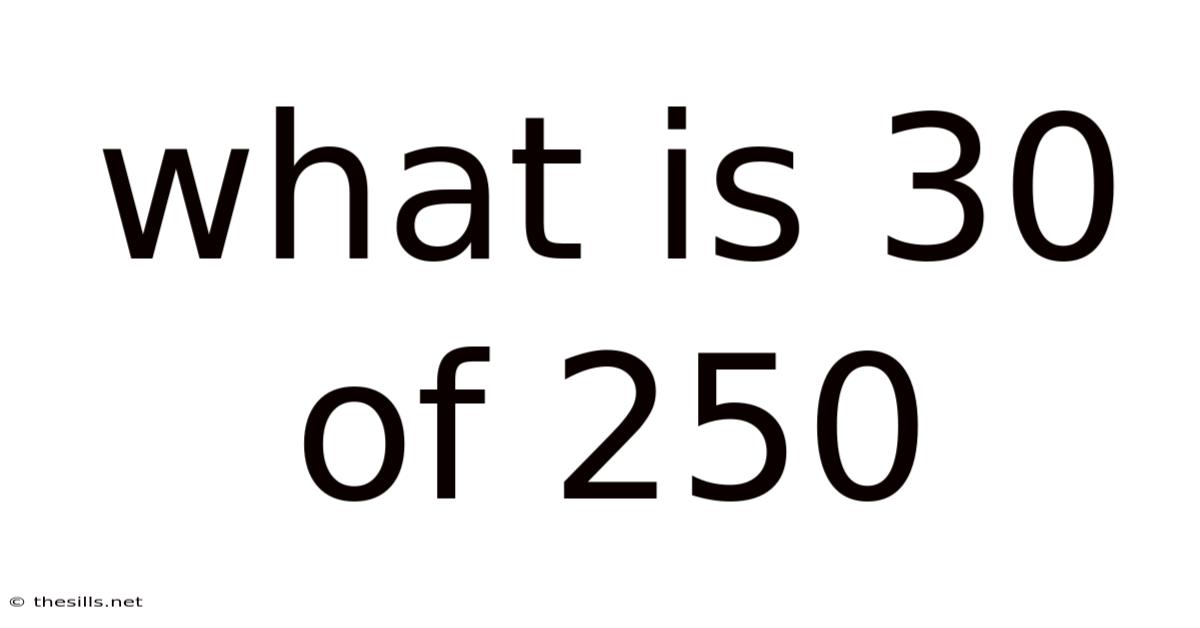
Table of Contents
What is 30% of 250? Understanding Percentages and Their Applications
Finding 30% of 250 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial reports. This article will not only answer the question "What is 30% of 250?" but will also delve into the methods for calculating percentages, explore their real-world applications, and address some frequently asked questions.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ("per cent" from Latin). Therefore, 30% means 30 out of 100, or 30/100, which simplifies to 3/10 as a fraction and 0.3 as a decimal.
Understanding this fundamental concept is key to solving percentage problems. Many real-world scenarios involve finding a percentage of a given number. For example, calculating sales tax, discounts, interest rates, or even analyzing statistical data often requires determining a percentage of a total value.
Calculating 30% of 250: Three Methods
There are several ways to calculate 30% of 250. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the given number.
-
Convert the percentage to a decimal: 30% = 30/100 = 0.30
-
Multiply the decimal by the number: 0.30 x 250 = 75
Therefore, 30% of 250 is 75.
Method 2: Using Fractions
This method involves converting the percentage to a fraction and then performing the multiplication.
-
Convert the percentage to a fraction: 30% = 30/100
-
Simplify the fraction (if possible): 30/100 simplifies to 3/10
-
Multiply the fraction by the number: (3/10) x 250 = 75
Again, we arrive at the answer: 30% of 250 is 75.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We set up a proportion where one ratio represents the percentage and the other represents the unknown value.
-
Set up the proportion: 30/100 = x/250 (where 'x' represents 30% of 250)
-
Cross-multiply: 30 x 250 = 100x
-
Solve for x: 7500 = 100x => x = 7500/100 => x = 75
This method reinforces the underlying concept of percentages as ratios. It demonstrates that 30 is to 100 as x is to 250.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly useful in various aspects of daily life and professional fields. Here are some examples:
-
Sales and Discounts: Stores often advertise discounts as percentages (e.g., "30% off"). Understanding percentage calculations allows consumers to quickly determine the actual price reduction. For example, a 30% discount on a $250 item results in a $75 discount, leaving a final price of $175 ($250 - $75).
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount requires finding the percentage of the taxable amount.
-
Interest Rates: Interest earned on savings accounts or paid on loans is calculated as a percentage of the principal amount. Understanding percentage calculations is vital for managing personal finances and understanding loan terms.
-
Tips and Gratuities: Calculating tips in restaurants or service charges often involves finding a percentage of the total bill.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions, frequencies, and changes in data. For example, understanding the percentage change in sales figures over time provides valuable insights for businesses.
-
Financial Reporting: Financial statements frequently use percentages to express ratios and trends. Analyzing these percentages helps investors and stakeholders assess a company's financial health.
-
Science and Engineering: Percentage calculations are used extensively in scientific experiments and engineering designs to express concentrations, efficiencies, and error rates.
Beyond the Basics: Calculating Percentage Increase and Decrease
While finding a percentage of a number is fundamental, many real-world scenarios involve calculating percentage increases or decreases. For example:
-
Percentage Increase: Suppose a product's price increased from $200 to $250. To calculate the percentage increase, we first find the difference ($250 - $200 = $50), then divide the difference by the original price ($50/$200 = 0.25), and finally multiply by 100 to express it as a percentage (0.25 x 100 = 25%). The price increased by 25%.
-
Percentage Decrease: If the price decreased from $250 to $200, we follow a similar process. The difference is $50, and we divide this by the original price ($250) to get 0.2. Multiplying by 100, we find a 20% decrease.
Frequently Asked Questions (FAQs)
Q: How do I calculate a different percentage of 250?
A: Simply replace 30% with the desired percentage. Follow the same steps outlined above, using either the decimal equivalent, fraction, or proportion method. For instance, to find 15% of 250, you would calculate 0.15 x 250 = 37.5.
Q: What if the percentage is greater than 100%?
A: A percentage greater than 100% means the result will be larger than the original number. For example, 150% of 250 is calculated as 1.5 x 250 = 375. This is often used to represent growth or increases exceeding the original value.
Q: Are there any online calculators for percentage calculations?
A: Yes, many online calculators are available that can perform percentage calculations quickly and easily. These tools can be particularly helpful for complex percentage problems or when speed is important. However, understanding the underlying principles remains essential for comprehending the results and applying them effectively.
Conclusion
Calculating 30% of 250, resulting in 75, is a seemingly simple calculation, but it represents a core concept in mathematics and its applications. Mastering percentage calculations is essential for navigating various aspects of daily life, from personal finances to professional endeavors. By understanding the different methods and their applications, you can confidently tackle percentage problems and interpret data expressed as percentages in various contexts. Remember, the key is to understand the underlying concept of percentages as fractions or ratios out of 100. This understanding forms the basis for solving all types of percentage problems efficiently and accurately.
Latest Posts
Latest Posts
-
1 50 Micrometers To Square Meters
Sep 14, 2025
-
What Is 5 Of 36000
Sep 14, 2025
-
Ln X 1 Lnx 2
Sep 14, 2025
-
Mushrooms Are Autotrophs Or Heterotrophs
Sep 14, 2025
-
Element 14 In Periodic Table
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.