What Is 3/5 Of 15
thesills
Sep 11, 2025 · 5 min read
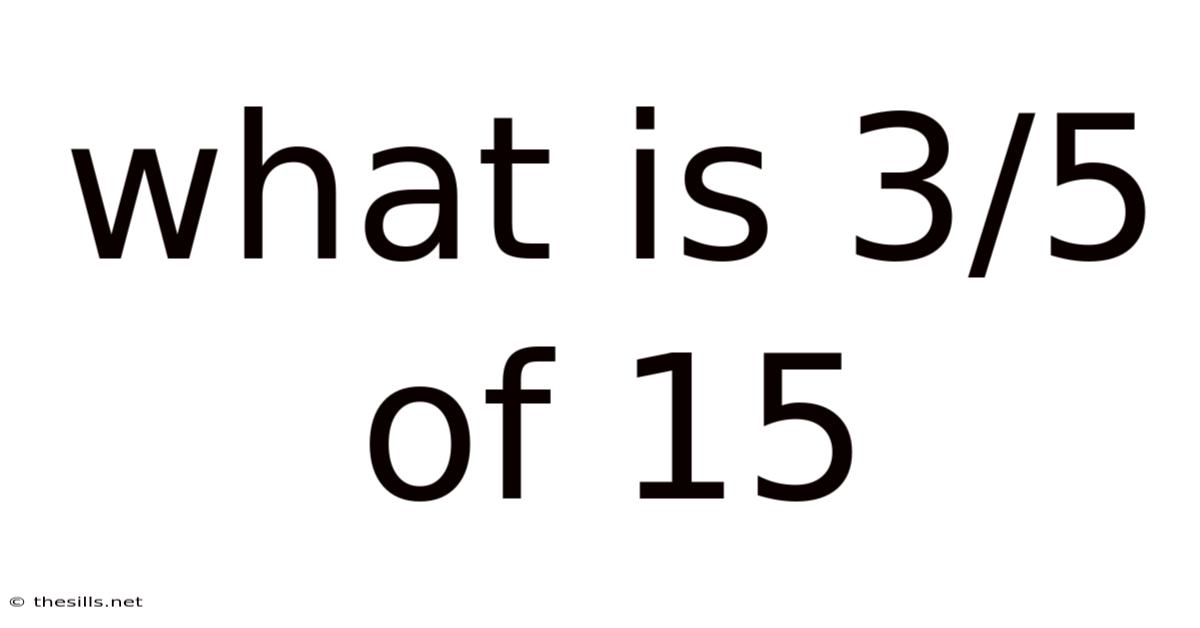
Table of Contents
What is 3/5 of 15? A Deep Dive into Fractions and Their Applications
Finding 3/5 of 15 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this problem unlocks a deeper comprehension of fractions, their practical applications, and their importance in various fields, from baking to engineering. This article will not only provide the answer but also delve into the underlying concepts, exploring different methods of calculation and showcasing the broader relevance of fractional arithmetic.
Introduction: Understanding Fractions and Their Components
Before we tackle the problem of finding 3/5 of 15, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main components:
- Numerator: The top number (in this case, 3) represents the number of parts we're considering.
- Denominator: The bottom number (in this case, 5) represents the total number of equal parts the whole is divided into.
Therefore, 3/5 signifies three out of five equal parts of a whole. Understanding this fundamental concept is crucial for grasping various fractional operations.
Method 1: Multiplication – The Direct Approach
The most straightforward method to find 3/5 of 15 is through multiplication. We can express "of" as multiplication. So, "3/5 of 15" translates to (3/5) * 15.
To perform this calculation:
- Multiply the numerator by the whole number: 3 * 15 = 45
- Divide the result by the denominator: 45 / 5 = 9
Therefore, 3/5 of 15 is 9.
Method 2: Finding the Fraction of One and Scaling Up
Another approach is to first determine what 1/5 of 15 is, and then multiply by 3 to find 3/5.
- Find 1/5 of 15: 15 / 5 = 3
- Multiply by the numerator: 3 * 3 = 9
This method provides a step-by-step breakdown, making the calculation more intuitive, especially for those less confident with fractions. Again, we arrive at the answer: 9.
Method 3: Visual Representation – A Concrete Approach
Visual aids can be particularly helpful in understanding fractions, especially for beginners. Imagine a rectangle divided into five equal parts. Shading three of these parts visually represents 3/5. If the entire rectangle represents 15, each part represents 15/5 = 3. Since we're interested in three parts, the answer is 3 * 3 = 9. This method reinforces the conceptual understanding of the fraction.
The Significance of Understanding Fractions: Real-World Applications
The seemingly simple calculation of 3/5 of 15 has far-reaching implications. Fractions are fundamental to countless areas of life and work:
-
Cooking and Baking: Recipes often involve fractional measurements. Understanding fractions is essential for accurately measuring ingredients and ensuring consistent results. For instance, a recipe might call for 2/3 cup of flour or 1/4 teaspoon of salt.
-
Construction and Engineering: Engineers use fractions extensively in blueprints and calculations, ensuring precision and accuracy in building structures, designing machinery, or creating intricate components. Understanding ratios and proportions, both intimately linked to fractions, is critical in ensuring structural integrity and functionality.
-
Finance and Economics: Fractions are used constantly in financial calculations, including interest rates, stock prices, and budgeting. For example, calculating discounts, understanding loan terms, or analyzing financial statements all rely heavily on fractional arithmetic.
-
Data Analysis and Statistics: Fractions and percentages (which are simply fractions expressed as a part of 100) are ubiquitous in data analysis and statistics. Understanding proportions and ratios allows us to interpret data effectively and draw meaningful conclusions.
-
Everyday Life: From dividing a pizza among friends to understanding sales discounts, fractions permeate our daily lives. The ability to work comfortably with fractions enhances our problem-solving skills and allows us to make informed decisions in numerous situations.
Expanding the Concept: Working with More Complex Fractions
While finding 3/5 of 15 is relatively straightforward, the principles involved extend to more complex fractional calculations. Consider the following example: What is 2/3 of 7/8?
This requires multiplying the numerators and denominators separately:
(2/3) * (7/8) = (27) / (38) = 14/24
This fraction can then be simplified by dividing both the numerator and denominator by their greatest common divisor (2):
14/24 = 7/12
Mastering this type of calculation is crucial for tackling advanced mathematical concepts and real-world problems involving proportions and ratios.
Frequently Asked Questions (FAQ)
-
What if the number isn't easily divisible by the denominator? If the whole number isn't perfectly divisible by the denominator, you'll end up with a fraction as your answer. For example, 3/5 of 17 would be (3 * 17) / 5 = 51/5, which can be expressed as a mixed number (10 1/5) or a decimal (10.2).
-
Can I use decimals instead of fractions? Yes, you can convert the fraction to a decimal before multiplying. 3/5 is equal to 0.6. So, 3/5 of 15 is 0.6 * 15 = 9. However, understanding the fractional representation is vital for many applications.
-
Why is understanding fractions so important? Fractions represent parts of a whole, and this concept is fundamental to numerous aspects of mathematics and its applications in various fields. Proficiency in fractional arithmetic is a cornerstone of mathematical literacy.
Conclusion: Mastering Fractions – A Foundation for Success
Finding 3/5 of 15, while seemingly simple, provides a springboard for understanding the broader world of fractions. This seemingly basic calculation underlines the importance of mastering fractional arithmetic, a skill with extensive applications across numerous disciplines. From cooking to engineering, finance to data analysis, the ability to work confidently with fractions empowers us to solve problems, make informed decisions, and navigate a world filled with numerical complexities. By understanding the underlying concepts and practicing different calculation methods, we build a strong mathematical foundation that will serve us well throughout life. So, remember that next time you encounter a fractional problem, you're not just solving an equation; you're unlocking a gateway to a deeper understanding of the world around you.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3/5 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.