What Is 1/6 + 1/8
thesills
Sep 13, 2025 · 6 min read
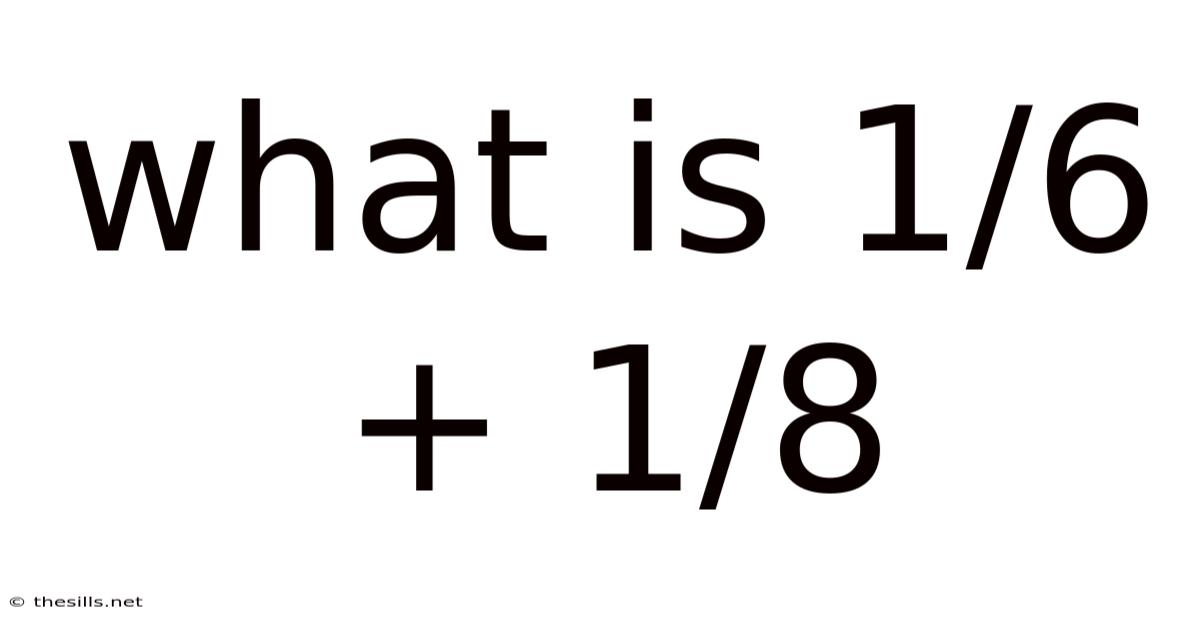
Table of Contents
Decoding Fractions: A Comprehensive Guide to Solving 1/6 + 1/8
Adding fractions might seem daunting at first glance, especially when the denominators (the bottom numbers) are different. This article provides a comprehensive guide to solving the equation 1/6 + 1/8, explaining the process step-by-step and exploring the underlying mathematical principles. We’ll delve into the concept of finding a common denominator, simplifying fractions, and applying these concepts to more complex fraction addition problems. By the end, you'll not only know the answer to 1/6 + 1/8 but also possess the skills to confidently tackle similar fraction addition problems.
Understanding Fractions: A Quick Recap
Before we dive into the solution, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/6, the numerator (1) signifies we have one part, and the denominator (6) signifies the whole is divided into six equal parts.
Finding a Common Denominator: The Key to Adding Fractions
The crucial step in adding fractions with different denominators is finding a common denominator. This is a number that is a multiple of both denominators. In our case, we need a common denominator for 6 and 8. One way to find this is by listing the multiples of each number:
- Multiples of 6: 6, 12, 18, 24, 30, 36…
- Multiples of 8: 8, 16, 24, 32, 40…
Notice that 24 appears in both lists. Therefore, 24 is a common denominator for 6 and 8. While other common denominators exist (48, 72, etc.), 24 is the least common denominator (LCD), making the calculations simpler. Finding the LCD can sometimes be challenging with larger numbers, and techniques like prime factorization can be helpful for more complex scenarios. However, for simpler cases, listing the multiples often suffices.
Converting Fractions to Equivalent Fractions
Now that we have our common denominator (24), we need to convert both 1/6 and 1/8 into equivalent fractions with a denominator of 24. To do this, we ask ourselves: "What number multiplied by the original denominator gives us 24?"
- For 1/6: 24 ÷ 6 = 4. Therefore, we multiply both the numerator and denominator of 1/6 by 4: (1 x 4) / (6 x 4) = 4/24.
- For 1/8: 24 ÷ 8 = 3. Therefore, we multiply both the numerator and denominator of 1/8 by 3: (1 x 3) / (8 x 3) = 3/24.
Remember, multiplying both the numerator and denominator by the same number doesn't change the value of the fraction; it simply expresses it in a different form.
Adding the Equivalent Fractions
Now that both fractions have the same denominator, we can add them:
4/24 + 3/24 = (4 + 3) / 24 = 7/24
Therefore, 1/6 + 1/8 = 7/24.
Simplifying Fractions (If Necessary)
In this case, 7/24 is already in its simplest form. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. If we had obtained a fraction like 12/24, we would simplify it by dividing both the numerator and denominator by their greatest common factor (which is 12 in this case), resulting in 1/2.
A Deeper Dive: The Mathematical Principles Behind Fraction Addition
The process of adding fractions hinges on the fundamental concept of equivalence. When we convert fractions to a common denominator, we are essentially finding equivalent fractions that represent the same portion of a whole but with a different representation. This allows us to add them directly, as they represent parts of the same whole.
The common denominator acts as a "unit of measure" for our fractions. Just as we can't directly add apples and oranges without converting them to a common unit (perhaps counting individual fruits), we cannot directly add fractions with different denominators. The common denominator ensures that we are adding parts of the same size.
Visualizing Fraction Addition
Imagine a pizza. If we divide the pizza into 6 equal slices and take one slice (1/6), and then we divide another pizza into 8 equal slices and take one slice (1/8), it's not immediately clear how to combine those slices to determine the total amount of pizza we have. However, if we re-slice both pizzas to have 24 equal slices (our common denominator), we can easily compare and combine the portions.
Solving More Complex Fraction Addition Problems
The same principles apply to more complex problems. For example, let's consider 2/5 + 3/10:
-
Find the LCD: The multiples of 5 are 5, 10, 15… and the multiples of 10 are 10, 20, 30… The LCD is 10.
-
Convert to equivalent fractions: 2/5 becomes (2 x 2) / (5 x 2) = 4/10. 3/10 remains as it is.
-
Add the fractions: 4/10 + 3/10 = 7/10
-
Simplify (if necessary): 7/10 is already in its simplest form.
Frequently Asked Questions (FAQ)
Q: What if I choose a common denominator that is not the least common denominator?
A: You can still obtain the correct answer, but the resulting fraction will need to be simplified. Using the least common denominator simplifies the calculation and reduces the need for simplification later.
Q: Can I add fractions with different numerators and denominators directly?
A: No. You must first find a common denominator and convert the fractions into equivalent fractions before adding them.
Q: What if the fractions are mixed numbers (a whole number and a fraction)?
A: Convert the mixed numbers into improper fractions (where the numerator is greater than or equal to the denominator) before applying the addition process. For instance, 2 1/2 would become 5/2.
Q: Are there other methods for finding the least common denominator (LCD)?
A: Yes, prime factorization is a powerful technique for finding the LCD, especially for larger numbers. It involves expressing each denominator as a product of prime numbers and then taking the highest power of each prime factor to determine the LCD.
Conclusion: Mastering Fraction Addition
Adding fractions, particularly those with unlike denominators, requires a systematic approach. By understanding the concepts of common denominators, equivalent fractions, and simplification, you can confidently solve a wide range of fraction addition problems. The process, while seemingly complex at first, becomes intuitive with practice. Remember to break down the problem into smaller, manageable steps and visualize the process to build a stronger understanding. With consistent practice, adding fractions will become second nature, empowering you to tackle more advanced mathematical concepts with greater ease and confidence. The solution to 1/6 + 1/8, as we have shown, is 7/24 – a result achieved through careful application of these fundamental principles.
Latest Posts
Latest Posts
-
1cm To 1 Unit Graph
Sep 13, 2025
-
Steric Strain Vs Torsional Strain
Sep 13, 2025
-
Shorter Diagonal Of A Rhombus
Sep 13, 2025
-
Synonym For The Word Fallible
Sep 13, 2025
-
Allen Biology Race Answer Key
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/6 + 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.