Twice A Number Is 4
thesills
Sep 17, 2025 · 5 min read
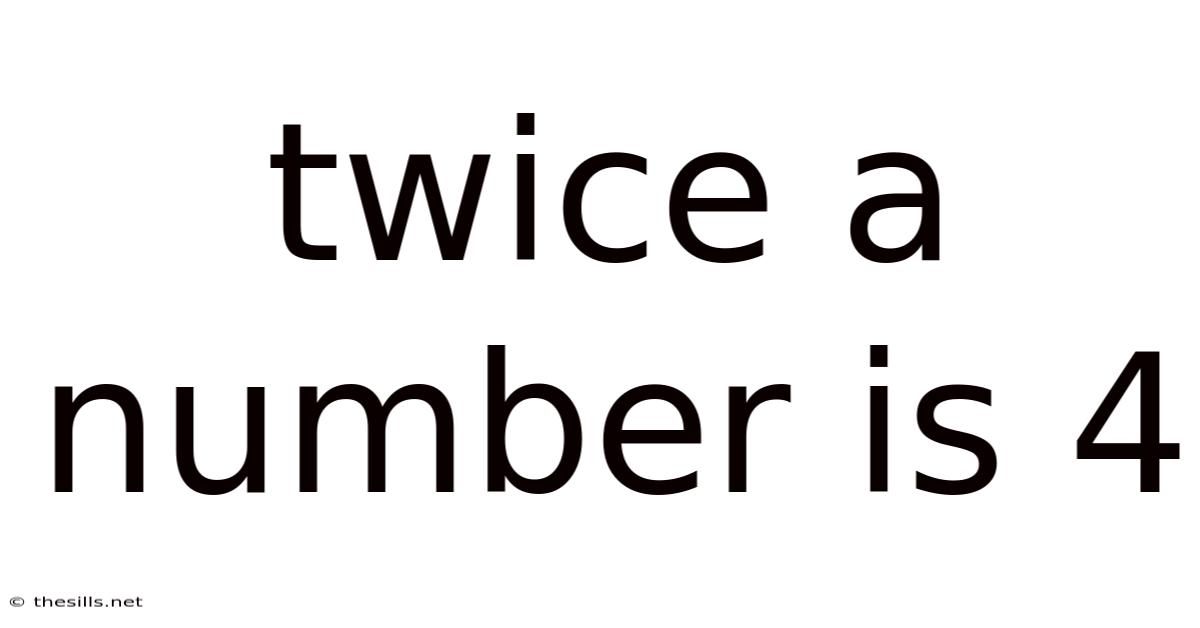
Table of Contents
Twice a Number is 4: Unpacking a Simple Equation and Exploring its Wider Implications
This seemingly simple equation, "Twice a number is 4," forms the bedrock of elementary algebra. While easily solvable, it opens doors to understanding fundamental mathematical concepts, problem-solving strategies, and even the elegance of mathematical representation. This article will delve into the solution, explore the underlying principles, and expand upon the broader implications of this seemingly simple equation. We will also tackle frequently asked questions and look at how this basic concept lays the foundation for more complex mathematical endeavors.
Understanding the Problem: Deconstructing "Twice a Number is 4"
The statement "Twice a number is 4" translates directly into a mathematical equation. Let's break it down:
- "A number": This represents an unknown value, which we typically denote with a variable, usually 'x' or 'y'. For simplicity, let's use 'x'.
- "Twice a number": This means two times the number, or 2 multiplied by x, written as 2x.
- "Is": This indicates equality, represented by the equals sign (=).
- "4": This is the result of doubling the unknown number.
Therefore, the complete equation becomes: 2x = 4
Solving the Equation: Finding the Value of x
Solving this equation involves isolating the variable 'x' to determine its value. We achieve this using inverse operations. Since 'x' is multiplied by 2, we perform the inverse operation – division – to both sides of the equation:
2x / 2 = 4 / 2
This simplifies to:
x = 2
Therefore, the number is 2. Twice 2 (2 x 2) equals 4, satisfying the initial statement. This simple solution showcases the power of algebraic manipulation to unravel unknown quantities.
Beyond the Solution: Exploring Fundamental Mathematical Concepts
This seemingly basic problem introduces several fundamental mathematical concepts:
-
Variables: The use of 'x' demonstrates the power of variables to represent unknown quantities. This is crucial in algebra and higher-level mathematics where we frequently deal with unknown values.
-
Equations: The equation 2x = 4 embodies the concept of an equation, a mathematical statement indicating equality between two expressions. Understanding equations is fundamental to solving a wide range of mathematical problems.
-
Inverse Operations: The solution process highlights the importance of inverse operations. Multiplication and division are inverse operations, as are addition and subtraction. Understanding these relationships is crucial for manipulating equations and isolating variables.
-
Equality: The equals sign signifies balance. Whatever is done to one side of the equation must be done to the other to maintain this balance and preserve the equality. This is a cornerstone of mathematical manipulation.
-
Problem-Solving: This simple problem provides a basic framework for problem-solving. It involves translating a word problem into a mathematical equation, manipulating the equation, and interpreting the solution within the context of the original problem.
Expanding the Scope: From Simple Equations to Complex Problems
While seemingly trivial, the equation 2x = 4 serves as a building block for more complex mathematical concepts. Understanding this fundamental equation provides a solid foundation for tackling more challenging problems involving:
-
Linear Equations: This simple equation is a type of linear equation, characterized by a single variable raised to the power of one. Understanding linear equations is critical for analyzing relationships between variables and solving real-world problems in various fields, including physics, engineering, and economics.
-
Systems of Equations: More complex problems often involve multiple equations with multiple variables. Solving these systems of equations requires a deeper understanding of algebraic manipulation and techniques such as substitution or elimination. The ability to solve simple equations like 2x = 4 is a prerequisite for solving these more intricate systems.
-
Inequalities: Instead of an equals sign, we might encounter inequalities (>, <, ≥, ≤). These introduce a new layer of complexity, requiring a different approach to solving for the unknown variable. However, the fundamental principles of manipulating equations remain the same.
-
Functions: In higher mathematics, we encounter functions, which describe relationships between variables. Understanding simple equations helps in grasping the concept of functions and their properties.
Real-World Applications: The Practical Significance of 2x = 4
Although presented in an abstract mathematical context, the principle behind “Twice a number is 4” has numerous real-world applications. Consider these scenarios:
-
Division of Resources: If you have 4 apples and want to divide them equally between two people, the equation 2x = 4 helps determine how many apples each person receives (x = 2).
-
Calculating Unit Prices: If two items cost $4, the equation helps find the price of a single item.
-
Scaling Recipes: Doubling a recipe often involves a simple multiplication. If a single serving requires a certain amount of an ingredient, and you want to make two servings, you'd use a similar equation to adjust the quantities.
-
Simple Physics Problems: Many basic physics problems involve proportional relationships which can be modeled with similar equations.
Frequently Asked Questions (FAQ)
Q1: Can this equation be solved using other methods?
A1: Yes, while the division method is the most straightforward, you could also use trial and error. However, for more complex equations, systematic algebraic manipulation is far more efficient and reliable.
Q2: What if the equation was 2x + 2 = 6?
A2: This introduces another term. We’d first subtract 2 from both sides, simplifying the equation to 2x = 4, which we’ve already solved. This demonstrates the need for a step-by-step approach for more complex equations.
Q3: What happens if the coefficient of x is not a whole number?
A3: The principle remains the same. For instance, in the equation 0.5x = 2, we would divide both sides by 0.5 to find x. The use of decimals or fractions doesn't change the underlying concept of inverse operations.
Q4: Is there a geometrical representation of this equation?
A4: Yes, you can represent this equation geometrically. The equation 2x = 4 can be visualized as finding the length of a rectangle with an area of 4 and a width of 2. The length (x) would then represent the solution (2).
Conclusion: The Enduring Significance of a Simple Equation
The equation "Twice a number is 4" may seem deceptively simple, but its significance extends far beyond its elementary solution. It serves as a gateway to understanding fundamental mathematical concepts, problem-solving techniques, and the elegance of algebraic manipulation. Mastering this basic equation lays the groundwork for tackling increasingly complex mathematical problems and applying mathematical principles to a wide range of real-world situations. The seemingly insignificant equation, therefore, holds the key to unlocking a world of mathematical possibilities. It highlights that even the most basic mathematical concepts can be both powerful and insightful, forming the foundation for more advanced understanding.
Latest Posts
Latest Posts
-
How To Find Additive Inverse
Sep 17, 2025
-
7 30 On A Clock
Sep 17, 2025
-
1 5 As A Whole Number
Sep 17, 2025
-
Rearrangement Property Of Rational Numbers
Sep 17, 2025
-
Spelled Forwards And Backwards Riddle
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Twice A Number Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.