Solve X 4 X 3
thesills
Sep 12, 2025 · 5 min read
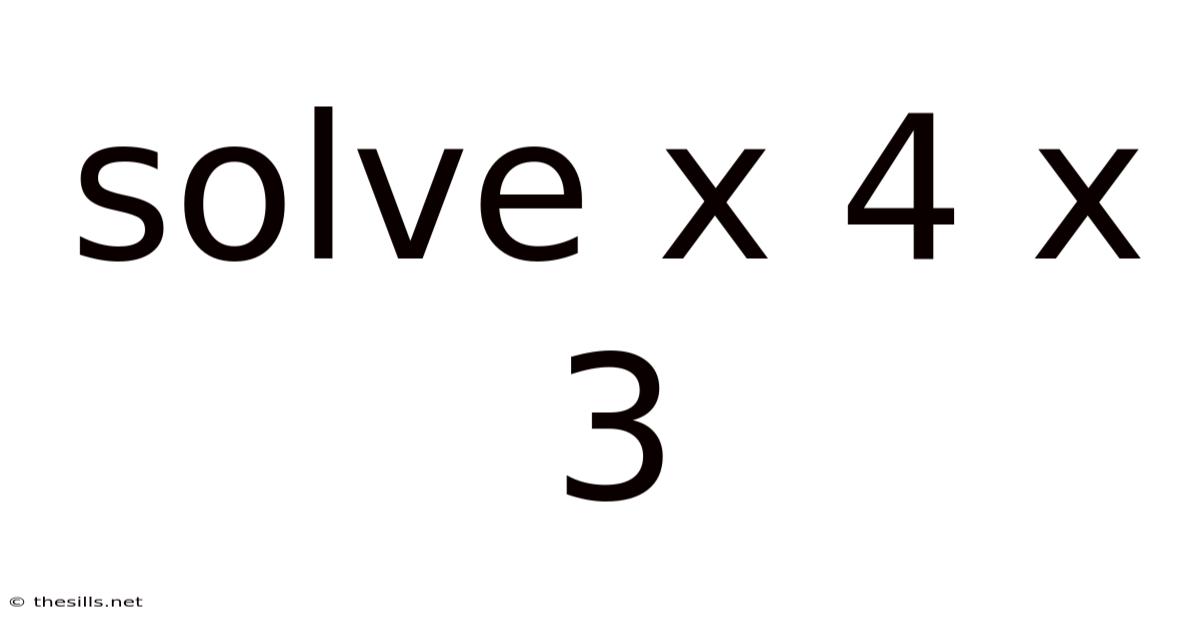
Table of Contents
Decoding the Mystery: Solving x⁴ = 3
This article delves into the intricacies of solving the equation x⁴ = 3, a seemingly simple equation that unveils fascinating concepts in algebra and complex numbers. We'll explore various methods for finding solutions, discuss the nature of these solutions, and provide a comprehensive understanding of the underlying mathematical principles. This guide is designed for students and anyone curious about tackling higher-order polynomial equations. Understanding this problem provides a strong foundation for tackling more complex mathematical challenges.
Introduction: Unveiling the Power of Fourth-Degree Equations
The equation x⁴ = 3 might seem straightforward at first glance. However, the challenge lies in understanding that this fourth-degree polynomial equation possesses four distinct solutions, not just one. These solutions involve the concept of complex numbers, expanding our understanding beyond the realm of real numbers. We'll explore how to find these solutions using various techniques, including:
- Taking the Fourth Root: The most intuitive approach.
- De Moivre's Theorem: A powerful tool for dealing with complex numbers raised to powers.
- Factorization Techniques: While less direct in this specific case, this method highlights important algebraic concepts.
By the end of this article, you'll not only know the solutions to x⁴ = 3 but also grasp the broader mathematical context and techniques applicable to solving similar problems.
Method 1: The Direct Approach – Taking the Fourth Root
The simplest way to begin is by directly taking the fourth root of both sides of the equation:
x⁴ = 3
√(x⁴) = √3
This gives us one real solution:
x = ³√3 ≈ 1.316
However, we know there are three more solutions. To find them, we need to delve into the world of complex numbers.
Method 2: Harnessing the Power of Complex Numbers and De Moivre's Theorem
Complex numbers are numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1). De Moivre's Theorem provides an elegant method for finding the roots of complex numbers. Let's express 3 in polar form:
3 = 3(cos 0 + i sin 0) (Note: We use 0 degrees here because 3 is a positive real number)
Now, to find the fourth roots, we use De Moivre's Theorem, which states that:
(cos θ + i sin θ)^n = cos(nθ) + i sin(nθ)
In our case, n = 4. We need to find θ such that:
cos(4θ) + i sin(4θ) = cos 0 + i sin 0
This means 4θ must be a multiple of 360 degrees (or 2π radians). Therefore:
4θ = 0 + 2kπ, where k is an integer (0, 1, 2, 3...)
Solving for θ:
θ = kπ/2, where k = 0, 1, 2, 3
Now, we can find the four roots:
- k = 0: x = ³√3 (cos 0 + i sin 0) = ³√3 ≈ 1.316 (This is our real solution)
- k = 1: x = ³√3 (cos(π/2) + i sin(π/2)) = ³√3i ≈ 1.316i
- k = 2: x = ³√3 (cos π + i sin π) = -³√3 ≈ -1.316
- k = 3: x = ³√3 (cos(3π/2) + i sin(3π/2)) = -³√3i ≈ -1.316i
These four solutions represent the complete solution set for x⁴ = 3.
Method 3: Algebraic Approach and Factorization (Less Direct)
While less efficient for this specific equation, exploring factorization methods provides deeper insight into polynomial equations. We can rewrite the equation as:
x⁴ - 3 = 0
This is a difference of squares, but not directly applicable. However, we can factor it using complex numbers:
(x² - ³√3)(x² + ³√3) = 0
This further breaks down into:
(x - ³√(³√3))(x + ³√(³√3))(x - i³√(³√3))(x + i³√(³√3)) = 0
This factorization reveals the same four roots we found using De Moivre's Theorem. While this method is less straightforward for this particular equation, it highlights the powerful connection between factorization and root-finding in polynomial algebra.
Understanding the Nature of the Solutions
The solutions to x⁴ = 3 consist of two real numbers and two purely imaginary numbers. They are symmetrically distributed in the complex plane, forming a cross pattern centered at the origin. This symmetry is a characteristic feature of the roots of equations involving even powers.
- Real Roots: ³√3 and -³√3
- Imaginary Roots: i³√3 and -i³√3
This symmetrical distribution arises directly from the use of De Moivre's Theorem and underscores the elegant relationship between the equation's degree and the number and nature of its solutions.
Frequently Asked Questions (FAQ)
-
Why are there four solutions? The Fundamental Theorem of Algebra states that a polynomial equation of degree 'n' has exactly 'n' roots (counting multiplicity). Since x⁴ = 3 is a fourth-degree polynomial, it has four solutions.
-
What if the exponent was different? The same principles apply, but the number of solutions and their distribution in the complex plane will change according to the degree of the polynomial. For example, x³ = 8 would have three solutions.
-
Can I use a calculator to solve this? While a calculator can approximate the numerical values of the solutions, understanding the underlying mathematical concepts and methods is crucial for a complete understanding.
-
Is there a general method for solving higher-order equations? There are general methods like the quartic formula for solving fourth-degree equations, but they are significantly more complex than the methods discussed here. For higher-degree polynomials, numerical methods are often more practical.
Conclusion: Beyond the Solution – A Deeper Understanding
Solving x⁴ = 3 goes beyond simply finding the four solutions. It's about understanding the interconnectedness of algebra, complex numbers, and the profound implications of the Fundamental Theorem of Algebra. We've explored various methods, highlighting the elegance of De Moivre's Theorem and the broader algebraic perspectives. The symmetrical distribution of solutions in the complex plane reveals a beautiful pattern reflecting the underlying mathematical structure. Mastering this seemingly simple equation provides a strong foundation for tackling more complex mathematical problems and builds a deeper appreciation for the richness and interconnectedness of mathematical concepts. Remember, the journey to understanding is as valuable as the destination of finding the solutions themselves.
Latest Posts
Latest Posts
-
Mediterranean Agriculture Intensive Or Extensive
Sep 12, 2025
-
Is Cd2 Paramagnetic Or Diamagnetic
Sep 12, 2025
-
Least Stable Conformation Of Cyclohexane
Sep 12, 2025
-
Three Properties Of A Liquid
Sep 12, 2025
-
Balloon And Hair Static Electricity
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Solve X 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.