Solve 2x 1 X 3
thesills
Sep 16, 2025 · 5 min read
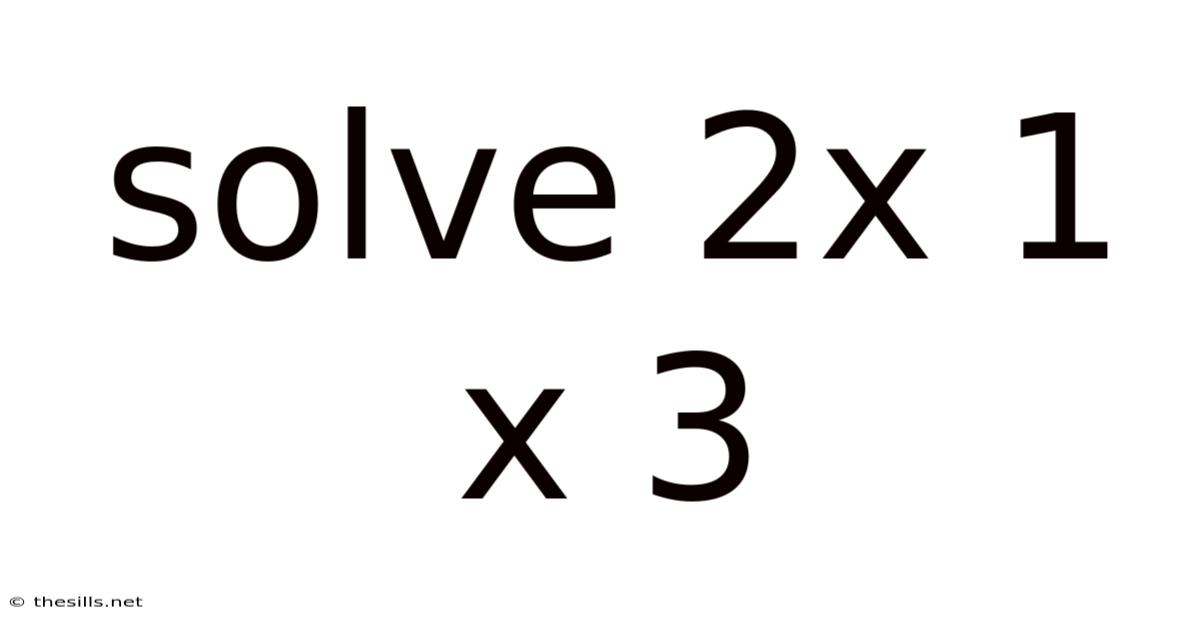
Table of Contents
Solving 2x + 1 = x + 3: A Step-by-Step Guide with Deeper Understanding
This article provides a comprehensive guide to solving the algebraic equation 2x + 1 = x + 3. We'll walk through the solution step-by-step, explaining the underlying principles of algebra involved. This isn't just about finding the answer; we'll explore the why behind each step, building a stronger foundation in algebraic problem-solving. Understanding this simple equation is a crucial stepping stone to tackling more complex algebraic problems in the future.
Understanding the Equation: Breaking Down the Basics
Before we dive into the solution, let's understand what the equation 2x + 1 = x + 3 actually represents. This is a linear equation, meaning the highest power of the variable (x) is 1. The equation shows that two expressions, 2x + 1 and x + 3, are equal. Our goal is to find the value of 'x' that makes this statement true.
- Variables: The 'x' represents an unknown quantity. We're trying to find the specific value of 'x' that satisfies the equation.
- Constants: The numbers 1 and 3 are constants. They are fixed values that don't change.
- Coefficients: The number 2 in '2x' is the coefficient of x. It represents the multiplier of the variable.
Solving the Equation: A Step-by-Step Approach
Now let's solve the equation 2x + 1 = x + 3. We'll use the principles of algebraic manipulation to isolate 'x' on one side of the equation. The key is to maintain balance—whatever operation we perform on one side of the equation, we must perform the same operation on the other side.
Step 1: Isolate the Variable Terms
Our first step is to gather all the terms containing 'x' on one side of the equation and the constant terms on the other side. We can achieve this by subtracting 'x' from both sides:
2x + 1 - x = x + 3 - x
This simplifies to:
x + 1 = 3
Step 2: Isolate the Variable
Now, we need to isolate 'x'. Since 1 is added to 'x', we subtract 1 from both sides of the equation:
x + 1 - 1 = 3 - 1
This simplifies to:
x = 2
Therefore, the solution to the equation 2x + 1 = x + 3 is x = 2.
Verification: Checking Our Solution
It's always a good practice to verify our solution by substituting the value of 'x' back into the original equation:
2x + 1 = x + 3
Substitute x = 2:
2(2) + 1 = 2 + 3
4 + 1 = 5
5 = 5
Since the equation holds true, our solution x = 2 is correct.
The Underlying Principles: A Deeper Dive into Algebraic Manipulation
The steps we took to solve the equation are based on fundamental algebraic principles:
- The Addition Property of Equality: If we add the same quantity to both sides of an equation, the equation remains balanced. We used this property when we subtracted 'x' from both sides.
- The Subtraction Property of Equality: If we subtract the same quantity from both sides of an equation, the equation remains balanced. We used this property when we subtracted 1 from both sides.
- The Simplification Principle: We combined like terms (terms with the same variable raised to the same power) to simplify the equation and isolate 'x'.
Expanding Our Understanding: Applications and Extensions
Solving linear equations like 2x + 1 = x + 3 is a foundational skill in algebra. It's used extensively in various fields, including:
- Physics: Solving for unknown variables in physics problems, such as calculating velocity, acceleration, or forces.
- Engineering: Designing and analyzing structures, circuits, and systems.
- Economics: Modeling economic relationships and making predictions.
- Computer Science: Developing algorithms and solving computational problems.
This simple equation also serves as a stepping stone to understanding more complex algebraic concepts, such as:
- Solving systems of equations: Finding the values of multiple variables that satisfy multiple equations simultaneously.
- Solving quadratic equations: Equations where the highest power of the variable is 2.
- Solving inequalities: Finding the range of values for a variable that satisfy an inequality (e.g., >, <, ≥, ≤).
Frequently Asked Questions (FAQs)
Q1: What if I subtracted 2x from both sides instead of x?
A1: That's perfectly acceptable! You would get:
2x + 1 - 2x = x + 3 - 2x
1 = -x + 3
Then, subtract 3 from both sides:
1 - 3 = -x
-2 = -x
Multiply both sides by -1:
x = 2
You arrive at the same solution, demonstrating that there's often more than one valid approach to solving an algebraic equation.
Q2: Can I add 1 to both sides before subtracting x?
A2: Yes, the order of operations isn't strictly defined in this case. You can perform the operations in a different sequence, as long as you maintain balance. However, the most efficient approach is generally to group like terms first.
Q3: What if the equation was more complex, with fractions or decimals?
A3: The same principles apply. You would still use the addition and subtraction properties of equality to isolate the variable, but you might need to perform additional steps, such as multiplying or dividing both sides by a constant to eliminate fractions or decimals.
Q4: What happens if there's no solution?
A4: In some cases, a linear equation might have no solution. This occurs when the variable terms cancel out, and you're left with a false statement (e.g., 2 = 5). Alternatively, a linear equation might have infinitely many solutions if the variable terms cancel out, and you're left with a true statement (e.g., 2 = 2).
Q5: How can I improve my skills in solving algebraic equations?
A5: Practice is key! Start with simple equations like the one we solved here, and gradually work your way up to more complex problems. Use online resources, textbooks, and practice exercises to hone your skills.
Conclusion: Mastering the Fundamentals of Algebra
Solving the equation 2x + 1 = x + 3 is a fundamental step in mastering algebra. By understanding the underlying principles and practicing the steps involved, you build a solid foundation for tackling more advanced algebraic problems. Remember, it's not just about finding the answer (x = 2); it's about understanding how we arrived at that answer and the broader mathematical concepts involved. This understanding will serve you well in your future mathematical endeavors. Keep practicing, and you'll soon find that solving algebraic equations becomes second nature.
Latest Posts
Latest Posts
-
Copper Oxide And Sulphuric Acid
Sep 16, 2025
-
Ph Of 0 01 M Hcl
Sep 16, 2025
-
Vant Hoff Factor Of Urea
Sep 16, 2025
-
Molecular Mass Of Zinc Carbonate
Sep 16, 2025
-
Equivalent Fraction Of 8 12
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Solve 2x 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.