Simplify X 2 1 2
thesills
Sep 14, 2025 · 6 min read
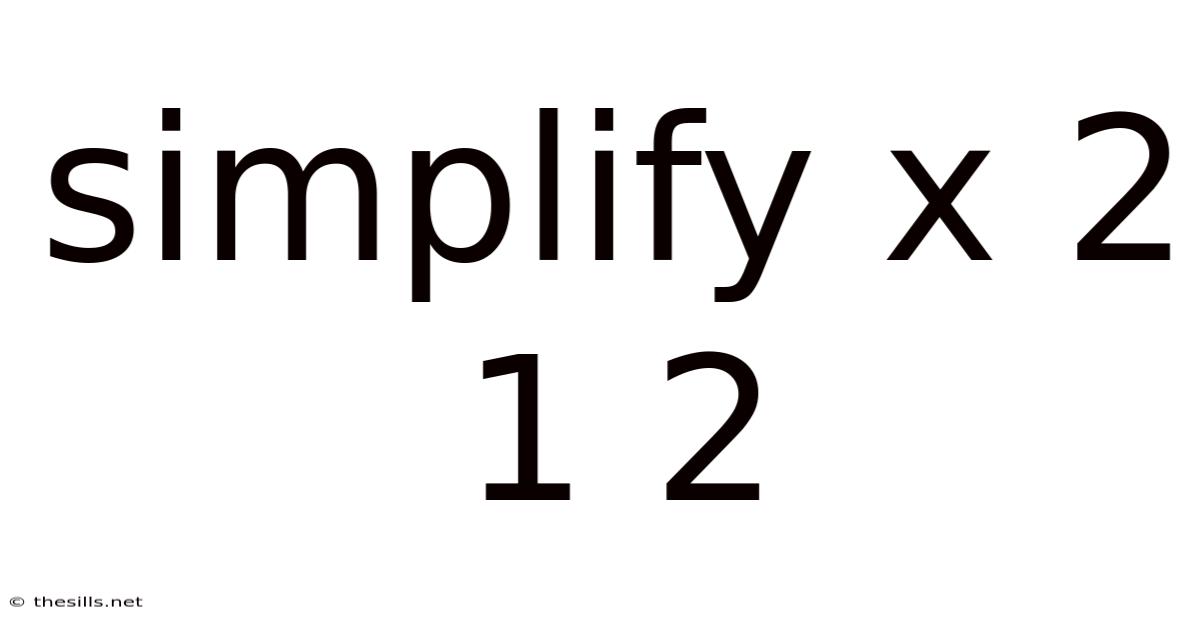
Table of Contents
Simplifying x² + 1/2x + 1/2: A Comprehensive Guide
This article provides a comprehensive guide to simplifying the quadratic expression x² + 1/2x + 1/2. We'll explore various methods, delve into the underlying mathematical principles, and address common questions related to simplifying and solving quadratic equations. Understanding this seemingly simple expression unlocks a deeper understanding of algebra and its applications. This guide is perfect for students learning about quadratic expressions and those looking to refresh their algebra skills.
I. Introduction: Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. The general form is ax² + bx + c, where a, b, and c are constants and a is not equal to zero. Our expression, x² + 1/2x + 1/2, fits this form with a = 1, b = 1/2, and c = 1/2.
Simplifying a quadratic expression often involves factoring, completing the square, or using the quadratic formula. The goal is to rewrite the expression in a more concise or manageable form, which can be useful for solving equations, graphing parabolas, or other mathematical manipulations.
II. Method 1: Factoring the Quadratic Expression
Factoring involves expressing the quadratic expression as a product of two simpler expressions. This method is not always possible for all quadratic expressions, but it's often the most straightforward when it works. Let's attempt to factor x² + 1/2x + 1/2.
We look for two numbers that add up to 1/2 (the coefficient of x) and multiply to 1/2 (the constant term). Finding these numbers might require some trial and error, or a more systematic approach using the quadratic formula (explained later). In this specific case, it's challenging to find rational numbers that satisfy these conditions. Therefore, factoring this particular quadratic expression directly is not easily achievable with simple rational numbers. This leads us to explore other methods.
III. Method 2: Completing the Square
Completing the square is a powerful technique that transforms a quadratic expression into a perfect square trinomial, plus a remaining constant. This method is always possible and is particularly useful for solving quadratic equations and understanding the parabola's vertex.
Here's how we complete the square for x² + 1/2x + 1/2:
-
Focus on the x terms: Consider the first two terms: x² + 1/2x.
-
Find the term to complete the square: To complete the square, we take half of the coefficient of x (which is 1/2), square it, and add it to the expression. Half of 1/2 is 1/4, and (1/4)² = 1/16.
-
Add and subtract: We add and subtract 1/16 within the expression: x² + 1/2x + 1/16 - 1/16 + 1/2.
-
Factor the perfect square trinomial: The first three terms now form a perfect square trinomial: (x + 1/4)².
-
Simplify the remaining constant: -1/16 + 1/2 = -1/16 + 8/16 = 7/16.
-
Final simplified form: The completed square form is (x + 1/4)² + 7/16.
Therefore, x² + 1/2x + 1/2 simplifies to (x + 1/4)² + 7/16. This form reveals that the parabola represented by this quadratic has a vertex at (-1/4, 7/16).
IV. Method 3: Using the Quadratic Formula
The quadratic formula is a powerful tool for finding the roots (or zeros) of a quadratic equation. While not directly simplifying the expression, it provides valuable information about the parabola and can be used indirectly to understand the expression's behavior.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
For our expression x² + 1/2x + 1/2, a = 1, b = 1/2, and c = 1/2. Substituting these values into the quadratic formula:
x = [-1/2 ± √((1/2)² - 4 * 1 * 1/2)] / (2 * 1) x = [-1/2 ± √(1/4 - 2)] / 2 x = [-1/2 ± √(-7/4)] / 2 x = [-1/2 ± (i√7)/2] / 2 where 'i' is the imaginary unit (√-1)
The roots are complex numbers because the discriminant (b² - 4ac = -7/4) is negative. This means the parabola does not intersect the x-axis. The presence of complex roots further confirms that simple factoring with real numbers isn't possible.
V. Geometric Interpretation: The Parabola
The expression x² + 1/2x + 1/2 represents a parabola. Completing the square reveals the vertex form, which allows us to easily identify the vertex and the parabola's orientation. The vertex form (x + 1/4)² + 7/16 shows that the vertex is at (-1/4, 7/16). Since the coefficient of the x² term (a = 1) is positive, the parabola opens upwards. This means the parabola is entirely above the x-axis, consistent with the complex roots found using the quadratic formula.
VI. Applications and Further Exploration
Understanding how to simplify quadratic expressions is crucial in various mathematical applications:
- Solving Quadratic Equations: Setting the expression equal to zero creates a quadratic equation, solvable using the methods discussed above.
- Graphing Parabolas: The vertex form obtained through completing the square allows for accurate graphing of the parabola.
- Calculus: Quadratic expressions are fundamental in calculus for finding derivatives and integrals.
- Physics and Engineering: Quadratic equations model many real-world phenomena, including projectile motion and the shape of certain structures.
VII. Frequently Asked Questions (FAQ)
-
Q: Can all quadratic expressions be factored easily? A: No. Many quadratic expressions cannot be factored using simple rational numbers. Completing the square or the quadratic formula are more general methods.
-
Q: What does a negative discriminant mean? A: A negative discriminant in the quadratic formula indicates that the quadratic equation has two complex roots (solutions involving the imaginary unit i). Geometrically, it means the parabola doesn't intersect the x-axis.
-
Q: Why is completing the square useful? A: Completing the square transforms the quadratic expression into vertex form, making it easy to identify the vertex and the parabola's orientation. It's also essential for certain integration techniques in calculus.
-
Q: What is the significance of the vertex of a parabola? A: The vertex represents the minimum (if the parabola opens upwards) or maximum (if the parabola opens downwards) point of the parabola. It's a crucial point for understanding the parabola's behavior.
VIII. Conclusion: Mastering Quadratic Expressions
Simplifying x² + 1/2x + 1/2, although seemingly straightforward, provides a gateway to understanding the rich world of quadratic expressions and their applications. By mastering the methods of factoring (when possible), completing the square, and applying the quadratic formula, you equip yourself with powerful tools for solving quadratic equations, graphing parabolas, and tackling more advanced mathematical concepts. Remember that each method offers a different perspective and can be advantageous depending on the context and the specific problem you are addressing. The ability to choose the most appropriate method demonstrates a deeper understanding of the underlying principles.
Latest Posts
Latest Posts
-
Ionic Compounds Containing Polyatomic Ions
Sep 14, 2025
-
Geometrical Meaning Of Scalar Product
Sep 14, 2025
-
Element With Atomic Number 15
Sep 14, 2025
-
Where Is Shifting Cultivation Practiced
Sep 14, 2025
-
Sodium Chloride Density G Ml
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Simplify X 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.