Simplify 1 2x 1 2
thesills
Sep 15, 2025 · 5 min read
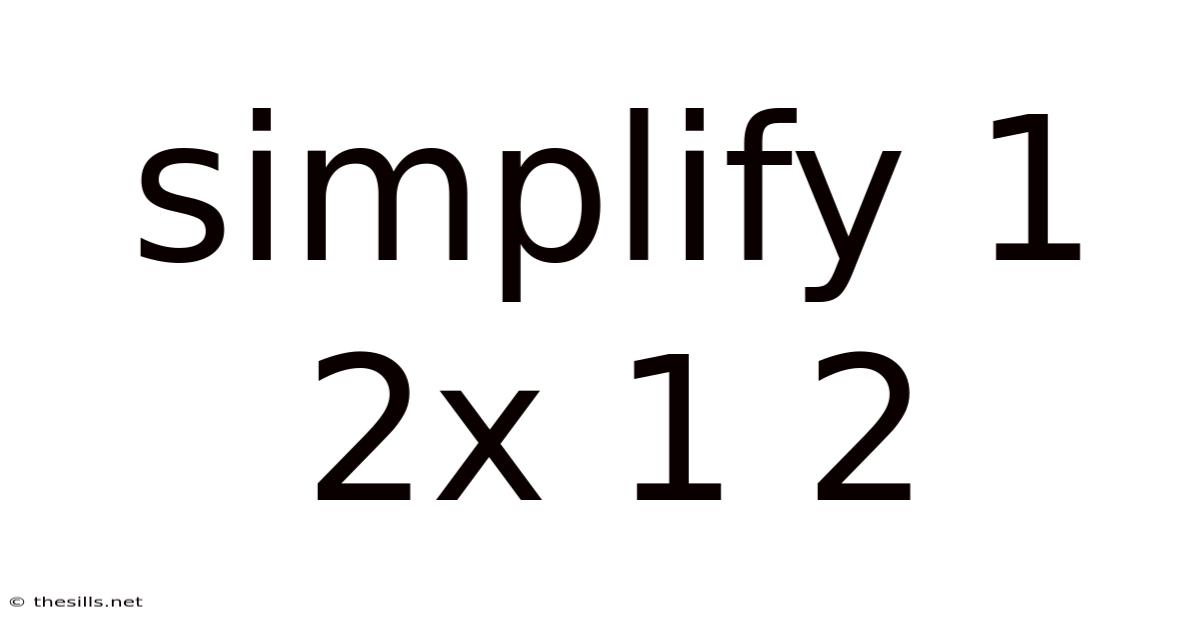
Table of Contents
Simplifying 1 + 2x + 1 + 2: A Comprehensive Guide
Understanding how to simplify algebraic expressions is a fundamental skill in mathematics. This article provides a comprehensive guide to simplifying the expression 1 + 2x + 1 + 2, explaining the steps involved and exploring the underlying mathematical principles. We'll cover the process step-by-step, address common misconceptions, and delve into the broader context of algebraic simplification. This guide is perfect for anyone looking to strengthen their foundational math skills, from students to anyone looking to brush up on their algebra.
Introduction: Understanding Algebraic Simplification
Algebraic simplification involves manipulating an expression to make it simpler and easier to understand. This often involves combining like terms, applying the distributive property, and factoring. The goal is to represent the same mathematical relationship in a more concise and efficient form. The expression 1 + 2x + 1 + 2 is a perfect example of an expression that can be significantly simplified.
Step-by-Step Simplification of 1 + 2x + 1 + 2
The key to simplifying this expression lies in identifying and combining like terms. Like terms are terms that have the same variable raised to the same power. In our expression, we have three types of terms:
- Constant terms: These are terms without any variables (1, 1, and 2).
- Variable terms: These are terms that contain a variable (2x).
Let's simplify the expression step-by-step:
-
Identify Like Terms: We have three constant terms (1, 1, and 2) and one variable term (2x).
-
Combine Constant Terms: Add the constant terms together: 1 + 1 + 2 = 4
-
Combine Variable Terms: There's only one variable term, 2x. It remains unchanged.
-
Write the Simplified Expression: Combine the simplified constant and variable terms to get the final simplified expression: 4 + 2x
Therefore, the simplified form of 1 + 2x + 1 + 2 is 2x + 4. It's crucial to note that the order of terms doesn't affect the value of the expression, so 4 + 2x is equally correct. However, it's a common convention in algebra to write the term with the variable first.
Understanding the Commutative and Associative Properties
The simplification process relies on fundamental properties of arithmetic:
-
Commutative Property: This property states that the order of addition or multiplication doesn't change the result. For example, 1 + 2 = 2 + 1, and 2 x 3 = 3 x 2. This property allows us to rearrange the terms in our expression for easier simplification.
-
Associative Property: This property states that the grouping of numbers in addition or multiplication doesn't change the result. For example, (1 + 2) + 3 = 1 + (2 + 3). This allows us to group like terms together before combining them.
In our example, we implicitly used both the commutative and associative properties when rearranging and grouping the constant terms:
1 + 2x + 1 + 2 = (1 + 1 + 2) + 2x = 4 + 2x
Common Mistakes to Avoid
A common mistake when simplifying expressions is incorrectly combining unlike terms. Remember, you can only add or subtract terms that have the same variable raised to the same power. For example, you cannot combine 2x and 4 because they are unlike terms. Another common error is incorrect application of the order of operations (PEMDAS/BODMAS). Always remember to follow the order of operations: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
Expanding the Concept: More Complex Expressions
The principles we applied to simplify 1 + 2x + 1 + 2 can be extended to more complex algebraic expressions. For instance, consider the following:
3x² + 5x + 2 + x² - 3x + 1
To simplify this:
-
Identify Like Terms: We have terms with
x², terms withx, and constant terms. -
Combine Like Terms:
x²terms: 3x² + x² = 4x²xterms: 5x - 3x = 2x- Constant terms: 2 + 1 = 3
-
Write the Simplified Expression: The simplified expression is
4x² + 2x + 3.
Explanation with Scientific Notation and Significant Figures
While this particular example doesn't directly involve scientific notation or significant figures, it's important to remember their relevance in the broader context of mathematical manipulation. Scientific notation is particularly useful when dealing with very large or very small numbers. Significant figures, on the other hand, represent the precision of a measurement and guide how we round our final answers to avoid implying a level of accuracy not supported by the input values. In more complex algebraic manipulations involving measured quantities, these concepts would be crucial for maintaining accuracy and clarity.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify 2x + 4 further?
- A: No, 2x + 4 is already in its simplest form. You cannot combine the variable term (2x) and the constant term (4) because they are unlike terms.
-
Q: What if the expression had more variables, like
1 + 2x + y + 1 + 2?- A: You would still follow the same principles. Combine like terms. In this case, you would combine the constant terms (1 + 1 + 2 = 4) and leave the variable terms (2x and y) as they are, resulting in a simplified expression of
2x + y + 4.
- A: You would still follow the same principles. Combine like terms. In this case, you would combine the constant terms (1 + 1 + 2 = 4) and leave the variable terms (2x and y) as they are, resulting in a simplified expression of
-
Q: What if the expression involved multiplication or division?
- A: You would need to follow the order of operations (PEMDAS/BODMAS) carefully. Multiplication and division would need to be performed before addition and subtraction.
-
Q: Why is it important to simplify algebraic expressions?
- A: Simplifying expressions makes them easier to understand and work with. Simplified expressions are easier to solve equations, graph functions, and perform other mathematical operations.
Conclusion: Mastering Algebraic Simplification
Simplifying algebraic expressions is a crucial skill in mathematics. By understanding the concept of like terms, the commutative and associative properties, and the order of operations, you can confidently simplify even complex expressions. This article has provided a comprehensive guide to simplifying 1 + 2x + 1 + 2, but the principles discussed here apply to a wide range of algebraic problems. Practicing regularly is key to mastering this fundamental skill and building a solid foundation for more advanced mathematical concepts. Remember to always double-check your work and ensure you're correctly combining like terms and following the order of operations. Consistent practice will build your confidence and proficiency in algebraic simplification.
Latest Posts
Latest Posts
-
What Is 50 Of 1
Sep 15, 2025
-
Where Are The Photosystems Located
Sep 15, 2025
-
Molecular Orbital Diagram For F2
Sep 15, 2025
-
What Is 75 Of 125
Sep 15, 2025
-
100g Glucose Equivalent In Food
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Simplify 1 2x 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.