Prime Numbers Less Than 30
thesills
Sep 14, 2025 · 7 min read
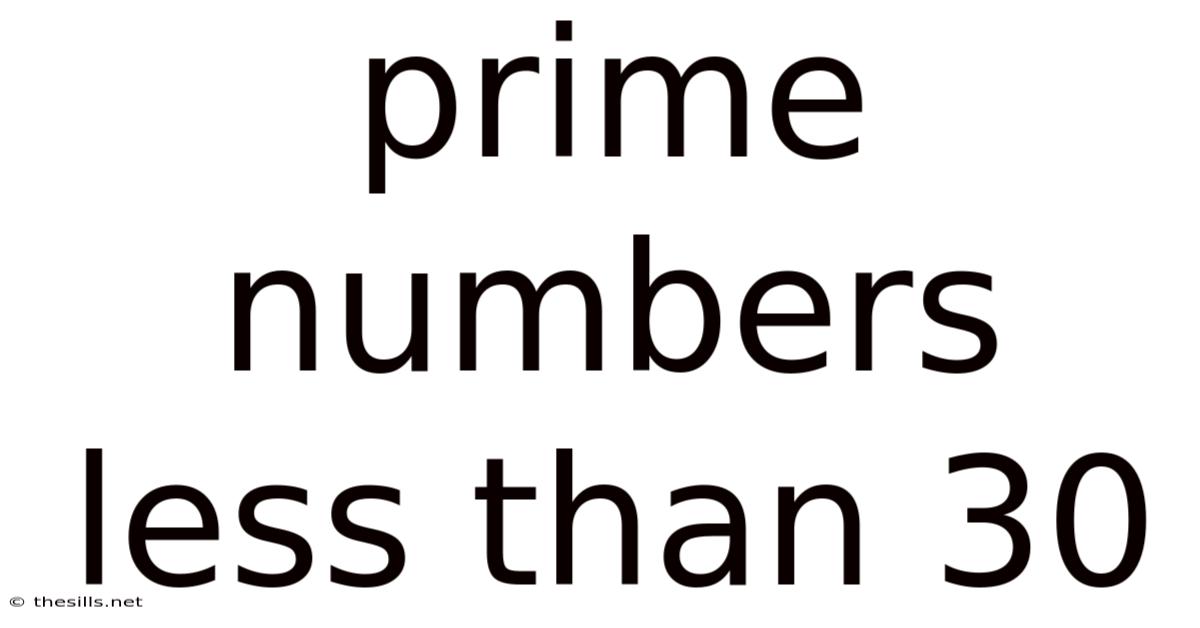
Table of Contents
Unveiling the Mysteries of Prime Numbers Less Than 30: A Deep Dive
Prime numbers, the fundamental building blocks of arithmetic, hold a captivating allure for mathematicians and number enthusiasts alike. Understanding prime numbers is key to grasping many concepts in number theory, cryptography, and computer science. This article delves into the fascinating world of prime numbers less than 30, exploring their properties, identification, and significance. We'll uncover why these seemingly simple numbers are so crucial, providing a comprehensive guide suitable for both beginners and those seeking a deeper understanding. By the end, you'll not only know all the prime numbers under 30 but also appreciate their fundamental role in mathematics.
What are Prime Numbers?
Before we dive into the specifics of primes less than 30, let's establish a firm foundation. A prime number is a natural number greater than 1 that has only two distinct positive divisors: 1 and itself. This means it cannot be expressed as a product of two smaller natural numbers. For instance, 7 is a prime number because it's only divisible by 1 and 7. Conversely, 6 is not a prime number because it's divisible by 1, 2, 3, and 6. Numbers like 6, which are divisible by numbers other than 1 and themselves, are called composite numbers. The number 1 is considered neither prime nor composite.
Identifying Prime Numbers Less Than 30: A Step-by-Step Approach
Let's systematically identify all prime numbers less than 30. We'll use the Sieve of Eratosthenes, a simple yet elegant algorithm for finding all prime numbers up to a specified integer.
1. List the Numbers: First, write down all the natural numbers from 2 to 29.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29
2. Eliminate Multiples:
- Start with the smallest prime number, 2. Cross out all multiples of 2 (excluding 2 itself): 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28.
- Next, move to the next uncrossed number, 3. Cross out all multiples of 3 (excluding 3 itself): 6, 9, 12, 15, 18, 21, 24, 27. Notice that some numbers (like 6 and 12) have already been crossed out.
- Continue this process with the next uncrossed number, 5. Cross out multiples of 5: 10, 15, 20, 25.
- Proceed with the next uncrossed number, 7. Cross out multiples of 7: 14, 21, 28.
3. The Remaining Numbers: The numbers that remain uncrossed are the prime numbers less than 30.
The Prime Numbers Less Than 30: A Complete List
Using the Sieve of Eratosthenes, we've identified the following prime numbers less than 30:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
These ten numbers form the bedrock for numerous mathematical explorations.
The Significance of Prime Numbers
The seemingly simple nature of prime numbers belies their profound importance in various fields:
-
Number Theory: Prime numbers are the fundamental building blocks of all integers. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors). This theorem underpins many advanced concepts in number theory.
-
Cryptography: Prime numbers are crucial in modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring large numbers into their prime factors. The larger the prime numbers used, the more secure the encryption.
-
Computer Science: Prime numbers play a role in various algorithms and data structures in computer science. For example, they're used in hash table design and in generating pseudo-random numbers.
-
Abstract Algebra: Prime numbers have deep connections to abstract algebra, specifically in the study of finite fields and modular arithmetic.
-
Distribution of Primes: The distribution of prime numbers, how they are spread out along the number line, is a subject of ongoing mathematical research. While the primes appear to be randomly scattered, sophisticated theorems like the Prime Number Theorem provide insights into their asymptotic distribution.
Exploring Properties of Prime Numbers Less Than 30
Let's explore some interesting properties specific to our list of prime numbers less than 30:
-
Twin Primes: Twin primes are pairs of prime numbers that differ by 2. In our list, we have (3, 5), (5, 7), (11, 13), and (17, 19). The existence of infinitely many twin primes is a famous unsolved problem in number theory.
-
Prime Gaps: The difference between consecutive prime numbers is called a prime gap. Analyzing prime gaps helps in understanding the distribution of primes. For instance, the prime gap between 23 and 29 is 6.
-
Sums and Differences: Exploring the sums and differences between primes in the list reveals patterns and relationships that can lead to further mathematical investigations.
-
Prime Factorization: Every composite number less than 30 can be expressed as a unique product of prime numbers from our list. For example: 12 = 2 x 2 x 3; 25 = 5 x 5; 28 = 2 x 2 x 7
Beyond the Basics: A Glimpse into Advanced Concepts
While this article focuses on prime numbers less than 30, it's important to note that the study of prime numbers extends far beyond this limited range. Here are a few advanced topics:
-
Mersenne Primes: These are prime numbers of the form 2<sup>p</sup> - 1, where p is also a prime number. The search for Mersenne primes is an ongoing area of research, with the largest known primes often being Mersenne primes.
-
Germain Primes: A Germain prime is a prime number p such that 2p + 1 is also prime.
-
Sophie Germain Identity: This identity relates the product of two sums of squares to another sum of squares. It's used in various number-theoretic proofs and applications.
-
The Riemann Hypothesis: This is one of the most important unsolved problems in mathematics. It relates the distribution of prime numbers to the zeros of the Riemann zeta function. A proof of the Riemann Hypothesis would have profound implications for our understanding of prime numbers and other areas of mathematics.
Frequently Asked Questions (FAQ)
Q: Is 1 a prime number?
A: No, 1 is neither prime nor composite. The definition of a prime number explicitly excludes 1.
Q: How many prime numbers are there?
A: There are infinitely many prime numbers. This was famously proven by Euclid in his Elements.
Q: Is there a largest prime number?
A: No. Since there are infinitely many prime numbers, there cannot be a largest one.
Q: How can I find larger prime numbers?
A: Finding large prime numbers involves sophisticated algorithms and significant computational resources. Specialized software and techniques are employed to identify and verify large primes. The search for ever-larger prime numbers is an ongoing area of research.
Q: What is the practical use of finding very large prime numbers?
A: The practical use primarily lies in cryptography. Large prime numbers are crucial for securing online communications and data. The difficulty of factoring large numbers into their prime components is the foundation of the security in many encryption systems.
Conclusion: The Enduring Mystery of Primes
Prime numbers, while seemingly simple, are far from mundane. Their fundamental role in mathematics and their applications in various fields underscore their importance. This exploration of prime numbers less than 30 serves as a stepping stone to a deeper understanding of this captivating area of mathematics. From the simple Sieve of Eratosthenes to the challenging Riemann Hypothesis, the study of primes offers a rich tapestry of mathematical exploration, inspiring curiosity and driving ongoing research into the fundamental building blocks of our number system. The mysteries surrounding prime numbers continue to fascinate mathematicians and offer countless opportunities for further discovery. The journey into the world of prime numbers is a journey of continuous learning and exploration.
Latest Posts
Latest Posts
-
Human Capital In A Sentence
Sep 14, 2025
-
What Is 25 Of 1200
Sep 14, 2025
-
Is H2 Diamagnetic Or Paramagnetic
Sep 14, 2025
-
2 15 On A Clock
Sep 14, 2025
-
Speed Of An Alpha Particle
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Prime Numbers Less Than 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.