Lim X 5 X 5
thesills
Sep 13, 2025 · 6 min read
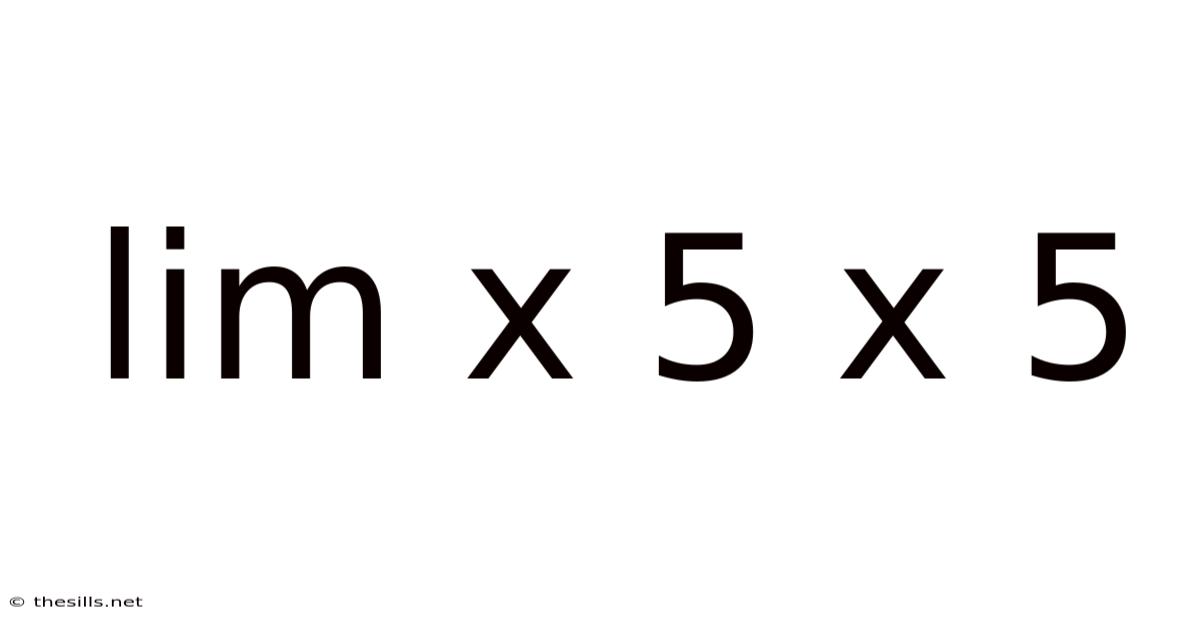
Table of Contents
Understanding the Limit: lim (x→5) (x - 5)
This article delves into the concept of limits in calculus, specifically examining the limit of the function f(x) = x - 5 as x approaches 5. We will explore the definition of a limit, the methods for evaluating limits, and the significance of this particular example in understanding fundamental calculus concepts. This exploration will be accessible to those with a basic understanding of algebra and will gradually build to a deeper understanding of limit theory. Learning about limits is crucial for understanding derivatives and integrals, which form the foundation of calculus.
Introduction to Limits
In calculus, a limit describes the behavior of a function as its input approaches a particular value. It's not necessarily about what happens at that specific value, but rather what the function approaches as the input gets arbitrarily close. We express this using the notation:
lim (x→a) f(x) = L
This reads as "the limit of f(x) as x approaches a is equal to L". This means that as x gets infinitely closer to 'a', the value of f(x) gets infinitely closer to 'L'. It's important to note that f(a) itself might not even be defined, or it might be different from L. The limit is concerned solely with the function's behavior around 'a'.
Evaluating the Limit: lim (x→5) (x - 5)
Let's now examine our specific problem: lim (x→5) (x - 5). This is a relatively straightforward limit. The function f(x) = x - 5 is a simple linear function. We can evaluate this limit using direct substitution.
Direct substitution is a method where we simply substitute the value that x is approaching into the function. In this case, we substitute x = 5 into f(x) = x - 5:
f(5) = 5 - 5 = 0
Therefore, the limit is:
lim (x→5) (x - 5) = 0
This result tells us that as x gets closer and closer to 5, the value of (x - 5) gets closer and closer to 0. This is intuitive since the expression (x - 5) represents the distance between x and 5. As x approaches 5, this distance approaches 0.
Graphical Representation
Visualizing the function can aid in understanding the limit. If we graph the function y = x - 5, we'll see a straight line with a slope of 1 and a y-intercept of -5. As x approaches 5 along the x-axis, the corresponding y-value on the line approaches 0 on the y-axis. This visual representation confirms our analytical result.
Epsilon-Delta Definition of a Limit
For a more rigorous understanding, we can use the epsilon-delta (ε-δ) definition of a limit. This definition provides a formal way to express the concept of a limit. The ε-δ definition states that for every ε > 0, there exists a δ > 0 such that if 0 < |x - a| < δ, then |f(x) - L| < ε.
In our case, a = 5, f(x) = x - 5, and L = 0. Let's choose an arbitrary ε > 0. We need to find a δ such that if 0 < |x - 5| < δ, then |(x - 5) - 0| < ε. Notice that |(x - 5) - 0| is simply |x - 5|. Therefore, we can choose δ = ε.
This shows that for any given ε, we can always find a δ (specifically, δ = ε) that satisfies the ε-δ definition. This formally proves that lim (x→5) (x - 5) = 0. While this formal proof may seem complex initially, understanding the concept is crucial for a deeper comprehension of limits.
Limits and Continuity
The concept of limits is closely related to continuity. A function is continuous at a point 'a' if the limit of the function as x approaches 'a' is equal to the function's value at 'a':
lim (x→a) f(x) = f(a)
In our example, f(x) = x - 5 is continuous at x = 5 because lim (x→5) (x - 5) = 0, and f(5) = 0. The limit exists, and it matches the function's value at that point.
However, it's crucial to understand that a limit can exist even if the function is not defined at the point in question. Consider the function:
g(x) = (x² - 25) / (x - 5)
This function is undefined at x = 5 because it leads to division by zero. However, we can simplify this function by factoring the numerator:
g(x) = (x - 5)(x + 5) / (x - 5) = x + 5 (for x ≠ 5)
Now, we can easily find the limit as x approaches 5:
lim (x→5) g(x) = lim (x→5) (x + 5) = 10
The limit exists and is equal to 10, even though the function g(x) is undefined at x = 5. This highlights a key difference between evaluating a function at a point and finding its limit as it approaches that point.
One-Sided Limits
While we've focused on two-sided limits (approaching 'a' from both left and right), it's important to understand one-sided limits. These are limits where we approach 'a' only from the left (x → a⁻) or only from the right (x → a⁺).
For our function f(x) = x - 5, both the left-hand limit and the right-hand limit as x approaches 5 are equal to 0. Only when these one-sided limits are equal can we conclude that the two-sided limit exists.
Limits Involving Infinity
The concept of limits extends beyond approaching a finite value. We can also examine limits as x approaches positive or negative infinity. For example:
lim (x→∞) (1/x) = 0
This means that as x becomes infinitely large, the value of 1/x approaches 0. Understanding limits involving infinity is crucial for analyzing the long-term behavior of functions.
Applications of Limits
Limits are fundamental to many areas of calculus and beyond. They are the foundation of:
- Derivatives: The derivative of a function at a point is defined as the limit of the difference quotient as the change in x approaches zero. This represents the instantaneous rate of change of the function.
- Integrals: Integrals are defined using limits of Riemann sums, which approximate the area under a curve.
- Series and Sequences: Limits are used to determine the convergence or divergence of infinite series and sequences.
Frequently Asked Questions (FAQ)
Q: What if direct substitution leads to an indeterminate form like 0/0?
A: If direct substitution results in an indeterminate form, you need to use algebraic manipulation (like factoring, simplifying, or rationalizing) or L'Hôpital's Rule (if applicable) to evaluate the limit.
Q: Are all functions continuous?
A: No, functions can be discontinuous at certain points. Discontinuities can be removable (like in the case of g(x) above), jump discontinuities, or infinite discontinuities.
Q: What is the significance of the epsilon-delta definition?
A: The epsilon-delta definition provides a rigorous mathematical framework for defining limits, avoiding ambiguity and providing a precise way to prove the existence and value of a limit.
Q: How are limits used in real-world applications?
A: Limits are essential in numerous real-world applications, including physics (velocity and acceleration), economics (marginal cost and revenue), and computer science (approximating complex calculations).
Conclusion
Understanding limits is a cornerstone of calculus and has far-reaching implications in various fields. While the concept might seem abstract at first, the fundamental idea is relatively simple: what value does a function approach as its input gets arbitrarily close to a specific value? The example of lim (x→5) (x - 5) = 0 serves as a straightforward introduction to this crucial concept. By mastering limits, you lay a solid foundation for further exploration of calculus and its diverse applications. Remember, the journey to understanding calculus is a gradual process, and persistent effort and practice will lead to a strong grasp of these fundamental concepts.
Latest Posts
Latest Posts
-
Molar Concentration Of Sulfuric Acid
Sep 13, 2025
-
Average Lifespan Of A Butterfly
Sep 13, 2025
-
A Psalm Of Life Paraphrase
Sep 13, 2025
-
Strength Of Solution In Chemistry
Sep 13, 2025
-
How Far Is 2000 Meters
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lim X 5 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.