Integral X Sin 2x Dx
thesills
Sep 15, 2025 · 5 min read
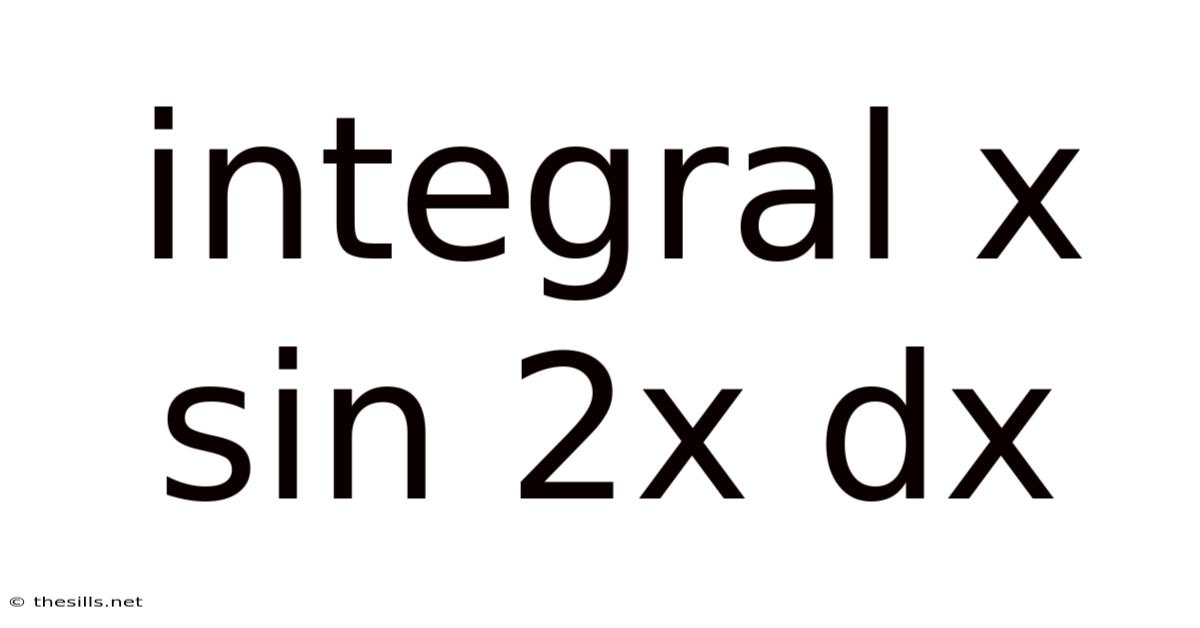
Table of Contents
Solving the Integral ∫x sin(2x) dx: A Comprehensive Guide
This article provides a step-by-step guide on how to solve the integral ∫x sin(2x) dx, a common problem encountered in calculus courses. We'll explore the process using integration by parts, a crucial technique for tackling integrals involving products of functions. Understanding this method will significantly enhance your ability to solve a wide range of complex integrals. We'll also delve into the underlying mathematical principles and offer explanations suitable for students of varying backgrounds.
Introduction: Understanding Integration by Parts
The integral ∫x sin(2x) dx involves the product of two functions: x and sin(2x). Direct integration is not straightforward. This is where integration by parts comes to the rescue. This technique is derived from the product rule of differentiation and provides a powerful method for evaluating integrals of this type. The formula for integration by parts is:
∫u dv = uv - ∫v du
where u and v are functions of x, and du and dv are their respective differentials. The key to successfully applying this method lies in choosing appropriate u and dv. A common mnemonic to help with this selection is "LIATE," which stands for Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, and Exponential functions. The function appearing earlier in this list is generally chosen as u.
Step-by-Step Solution: ∫x sin(2x) dx
Let's apply integration by parts to solve ∫x sin(2x) dx.
1. Choosing u and dv:
Following the LIATE rule, we choose:
- u = x => du = dx
- dv = sin(2x) dx => v = -1/2 cos(2x) (Remember to integrate dv to find v)
2. Applying the Integration by Parts Formula:
Now, substitute these values into the integration by parts formula:
∫x sin(2x) dx = uv - ∫v du = x(-1/2 cos(2x)) - ∫(-1/2 cos(2x)) dx
3. Simplifying and Integrating:
The integral becomes:
-1/2 x cos(2x) + 1/2 ∫cos(2x) dx
Now, integrate cos(2x):
∫cos(2x) dx = (1/2)sin(2x) + C (where C is the constant of integration)
Therefore, the integral simplifies to:
-1/2 x cos(2x) + 1/2 * (1/2)sin(2x) + C
4. Final Result:
The final solution to the integral ∫x sin(2x) dx is:
-1/2 x cos(2x) + 1/4 sin(2x) + C
Detailed Explanation of Each Step
Let's examine each step in more detail to solidify our understanding.
Step 1: Selecting u and dv
The choice of u and dv is crucial. If we had chosen u = sin(2x) and dv = x dx, the resulting integral would have been more complex than the original. The LIATE rule provides a helpful guideline, but experience will refine your intuition in selecting the optimal u and dv.
Step 2: Applying the Formula
The formula ∫u dv = uv - ∫v du is a direct application of the product rule in reverse. Understanding the derivation of this formula from the product rule enhances its comprehension.
Step 3: Simplification and Integration
This step involves simplifying the expression and performing a standard integral. The integral of cos(2x) requires a simple substitution or recognition of its standard integral form. Remember to include the constant of integration, C, which accounts for the family of antiderivatives.
Step 4: The Final Solution
The final solution is obtained by combining all the terms and presenting the result in a simplified and clear manner. This solution represents all possible antiderivatives of x sin(2x).
Verification Through Differentiation
A powerful way to verify the correctness of our integral solution is to differentiate the result. If the derivative matches the original integrand, our integration is correct. Let's differentiate our solution:
d/dx [-1/2 x cos(2x) + 1/4 sin(2x) + C]
Using the product rule and chain rule:
= [-1/2 cos(2x) + 1/2 x (2 sin(2x))] + 1/4 (2 cos(2x))
= -1/2 cos(2x) + x sin(2x) + 1/2 cos(2x)
= x sin(2x)
This matches our original integrand, confirming the accuracy of our solution.
Further Applications and Extensions
The integration by parts technique isn't limited to this specific example. It's widely applicable to integrals involving products of various functions, especially when dealing with trigonometric functions combined with polynomials or exponentials. Here are some examples of similar integrals that can be solved using the same method:
- ∫x cos(3x) dx
- ∫x² e^x dx
- ∫ln(x) dx (Here, let u = ln(x) and dv = dx)
- ∫x arctan(x) dx
Frequently Asked Questions (FAQ)
Q1: What if I choose u and dv differently?
A1: Choosing u and dv incorrectly might lead to a more complex integral than the original, making the problem harder to solve. While not necessarily wrong, it can be significantly less efficient. The LIATE rule helps guide you toward a more efficient selection.
Q2: Why is the constant of integration (C) important?
A2: The constant of integration, C, is crucial because the derivative of a constant is zero. Therefore, many functions can have the same derivative. The constant C represents this family of functions. Omitting C is a common mistake that should be avoided.
Q3: Can I use other integration techniques to solve this?
A3: While integration by parts is the most straightforward method for this particular integral, other advanced techniques might be applicable, but they would likely be more cumbersome.
Q4: How can I improve my skills in integration?
A4: Practice is key! Work through many examples, focusing on understanding the underlying principles rather than just memorizing formulas. Refer to textbooks and online resources for additional examples and explanations.
Conclusion: Mastering Integration by Parts
Solving the integral ∫x sin(2x) dx demonstrates the power and elegance of integration by parts. By systematically selecting u and dv, applying the formula, and carefully simplifying the resulting expression, we successfully solved a seemingly complex integral. Understanding this technique is fundamental to progressing in calculus and its numerous applications in science, engineering, and other fields. Remember that consistent practice and a strong grasp of the underlying principles are essential for mastering integration techniques and tackling more advanced problems. The process of solving integrals, while sometimes challenging, offers a rewarding intellectual exercise and a powerful tool for problem-solving.
Latest Posts
Latest Posts
-
X 1 2 X 1
Sep 15, 2025
-
X 2 5x 6 0
Sep 15, 2025
-
Ratio Of Radius To Circumference
Sep 15, 2025
-
D Glucose And D Fructose
Sep 15, 2025
-
50 Percent Off 50 Dollars
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Integral X Sin 2x Dx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.