Integral Of X Sin 1x
thesills
Sep 16, 2025 · 5 min read
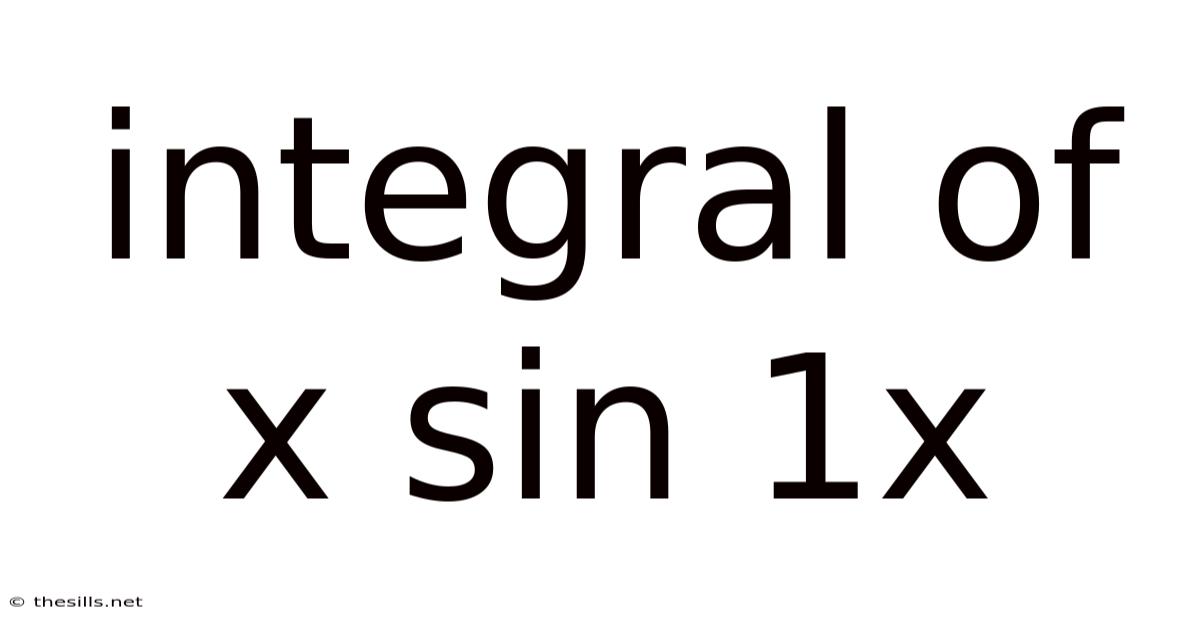
Table of Contents
Tackling the Integral of x sin(1/x): A Comprehensive Guide
The integral ∫x sin(1/x) dx presents a fascinating challenge in calculus. It's not immediately obvious how to approach this seemingly simple problem, as it doesn't yield readily to standard integration techniques like substitution or integration by parts. This article will guide you through a complete solution, exploring the nuances of the problem, offering a step-by-step approach, and delving into the underlying mathematical concepts. We'll also address common questions and misconceptions surrounding this integral.
Introduction: Why This Integral is Tricky
The integral ∫x sin(1/x) dx is challenging because the argument of the sine function, 1/x, creates a non-elementary integral. This means that the antiderivative cannot be expressed in terms of elementary functions (polynomials, trigonometric functions, exponential functions, logarithms, and their combinations). This characteristic requires us to employ a specific technique and understand its implications.
Step-by-Step Solution using Substitution and Integration by Parts
While the integral doesn't directly yield to a single technique, a clever combination of substitution and integration by parts will lead us to the solution. Let's break it down:
- Substitution: Let's begin by performing a substitution to simplify the expression. Let u = 1/x. This implies that x = 1/u, and dx = -1/u² du. Substituting these into our integral, we get:
∫x sin(1/x) dx = ∫(1/u) sin(u) (-1/u²) du = -∫sin(u)/u³ du
- Integration by Parts: Now we utilize integration by parts. Recall the formula for integration by parts: ∫u dv = uv - ∫v du. Let's choose:
- u = 1/u² (This choice might seem unusual, but it works beautifully in this context.)
- dv = sin(u) du
Therefore:
- du = -2/u³ du
- v = -cos(u)
Applying integration by parts:
-∫sin(u)/u³ du = -(1/u²)(-cos(u)) - ∫(-cos(u))(-2/u³) du = (cos(u)/u²) - 2∫(cos(u)/u³) du
-
Iterative Process: Observe that we have reduced the power of u in the denominator from 3 to 3 again in the second integral. This indicates a potential iterative process. However, this iterative approach doesn't lead to a closed-form solution using elementary functions. The integral ∫(cos(u)/u³) du is also non-elementary.
-
The Non-Elementary Nature: This highlights a crucial point: The integral ∫x sin(1/x) dx does not have a closed-form solution expressible in terms of elementary functions. The techniques we've employed, while helpful in simplifying the expression, don't ultimately provide a final, elementary antiderivative.
Exploring Alternative Approaches and Series Expansions
Since a closed-form solution isn't possible with elementary functions, we can explore alternative approaches:
- Power Series Expansion: We can express sin(u) using its Maclaurin series:
sin(u) = u - u³/3! + u⁵/5! - u⁷/7! + ...
Substituting this into our modified integral -∫sin(u)/u³ du:
-∫(u - u³/3! + u⁵/5! - u⁷/7! + ...)/u³ du = -∫(1/u² - 1/(3!u) + u²/5! - u⁴/7! + ...) du
Integrating term by term:
1/u + ln|u|/6 - u³/5! + u⁵/7! - … + C
Substituting back u = 1/x:
x + (ln|1/x|)/6 - 1/(120x³) + 1/(5040x⁵) - ... + C
This power series provides an approximation for the integral, but it's an infinite series, and thus not a closed-form solution. The accuracy of the approximation depends on the number of terms included.
- Numerical Integration Techniques: For practical applications, numerical methods such as the Trapezoidal rule, Simpson's rule, or more sophisticated techniques like Gaussian quadrature are commonly used to approximate the definite integral over a specified interval. These methods provide numerical estimates of the definite integral's value.
The Importance of Understanding Limits and Convergence
When working with infinite series representations, understanding convergence is critical. The power series we derived converges for certain values of x, and diverges for others. Determining the radius of convergence and the interval of convergence is important for ensuring the validity of the approximation.
Addressing Common Questions and Misconceptions
-
Is there a mistake in the calculations? No, the integral is genuinely non-elementary. The difficulty arises not from errors in calculation but from the inherent nature of the function.
-
Can a different substitution solve the problem? While different substitutions might simplify aspects of the integral, none will lead to a closed-form solution using only elementary functions.
-
Why is this integral so important? While this specific integral might not appear frequently in introductory calculus courses, its non-elementary nature highlights the limitations of elementary functions in representing all possible integrals. It's a valuable example that underscores the need for more advanced techniques and approximations in dealing with complex integrals. This problem often serves as an illustrative example in advanced calculus courses that deal with the theory of integration and special functions.
Conclusion: The Power of Approximation and Numerical Methods
The integral ∫x sin(1/x) dx serves as a prime example of a problem where the elegant closed-form solutions we often seek in introductory calculus are unavailable. Understanding this limitation doesn't diminish the problem's significance; instead, it underscores the importance of alternative approaches. Power series expansions and numerical integration techniques become indispensable tools for handling such integrals, providing accurate approximations and solutions applicable to various practical scenarios. This integral highlights the rich and complex landscape of calculus, urging us to explore beyond the confines of elementary functions and embrace the power of approximation and numerical methods. It also underscores the beauty of mathematics in its capacity to present seemingly simple problems that lead to deep insights into the theoretical underpinnings of calculus. This problem is not about finding a simple answer; it's about understanding the limits of techniques and the power of alternative approaches.
Latest Posts
Latest Posts
-
Vapor Pressure Of Diethyl Ether
Sep 16, 2025
-
Barriers Which Restrict Water Flow
Sep 16, 2025
-
Which Statement Best Describes Electrons
Sep 16, 2025
-
How Tall Is 168 Centimeters
Sep 16, 2025
-
How Many Atoms In Gold
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X Sin 1x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.