Integral Of 1 1 2x
thesills
Sep 15, 2025 · 5 min read
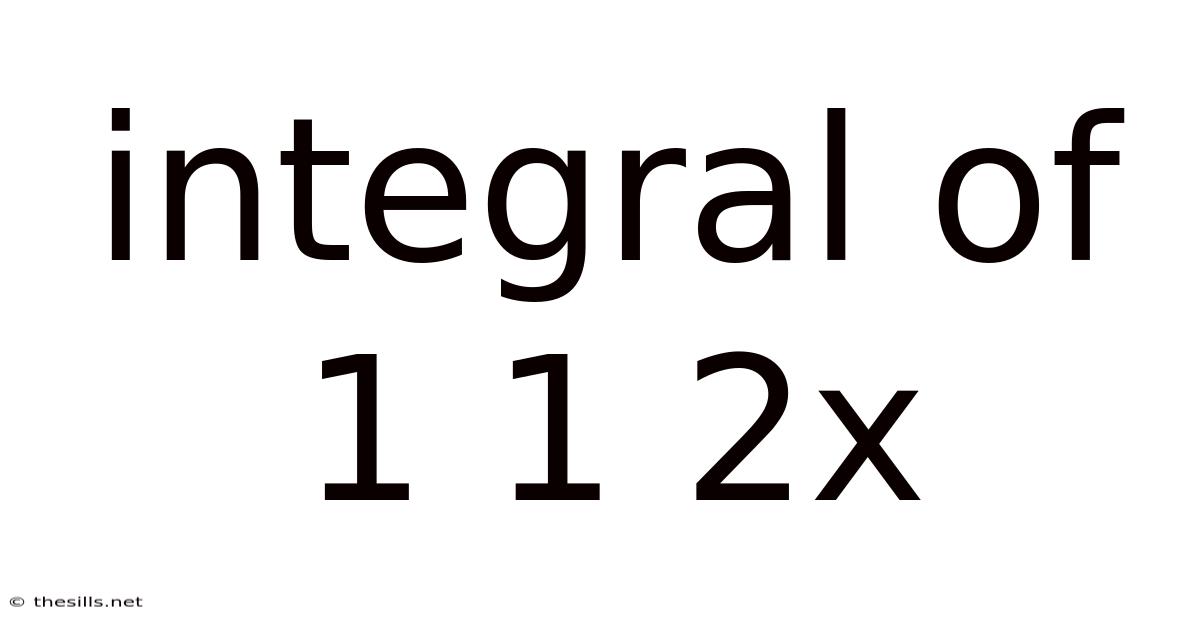
Table of Contents
Understanding and Solving the Integral of 1/(1+2x)
The integral ∫ 1/(1+2x) dx might seem intimidating at first glance, especially for those new to calculus. However, with a systematic approach and a solid understanding of basic integration techniques, this seemingly complex problem becomes surprisingly straightforward. This article will guide you through the process, explaining the steps involved, the underlying principles, and offering additional insights to solidify your understanding of integration.
Introduction: A Gentle Approach to Integration
Integration is fundamentally the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the function whose derivative is the given function. We are looking for a function, let's call it F(x), such that its derivative, F'(x), equals 1/(1+2x). The solution involves using a technique called u-substitution, a powerful method for simplifying integrals.
Step-by-Step Solution using U-Substitution
The key to solving this integral lies in the effective use of u-substitution. This method involves substituting a part of the integrand (the function being integrated) with a new variable, 'u', to simplify the expression. Here's how we apply it to our integral:
-
Choose your 'u': Let's choose u = 1 + 2x. This is a strategic choice because the derivative of this expression is relatively simple and present in the original integral.
-
Find 'du': Differentiating both sides of u = 1 + 2x with respect to x gives us du/dx = 2. Rearranging, we get du = 2dx.
-
Substitute: Now we substitute 'u' and 'du' into our original integral:
∫ 1/(1+2x) dx becomes ∫ (1/u) * (1/2) du
Notice that we have replaced (1+2x) with 'u' and 'dx' with 'du/2'. This simplifies the integral significantly.
-
Solve the Simplified Integral: The integral ∫ (1/u) * (1/2) du is now much easier to solve. We can pull the constant (1/2) outside the integral:
(1/2) ∫ (1/u) du
The integral of 1/u is the natural logarithm of the absolute value of u: ln|u| + C, where 'C' is the constant of integration.
-
Back-Substitute: Remember that u = 1 + 2x. Substituting this back into our solution, we get:
(1/2) ln|1 + 2x| + C
Therefore, the integral of 1/(1+2x) dx is (1/2) ln|1 + 2x| + C.
A Deeper Dive: Understanding the Natural Logarithm
The appearance of the natural logarithm (ln) in our solution requires a bit more explanation. The natural logarithm is the inverse function of the exponential function e<sup>x</sup>. Its presence here is not arbitrary; it's a direct consequence of the derivative of ln|x|, which is 1/x. This fundamental relationship is crucial to understanding many integration problems.
The absolute value sign, | |, around (1+2x) is essential because the logarithm is only defined for positive arguments. Including the absolute value ensures the expression is valid for all values of x.
Expanding the Horizons: Applications and Further Exploration
This seemingly simple integral has broad applications in various fields. For instance:
-
Exponential Growth and Decay: The integral is frequently encountered when solving differential equations modeling population growth, radioactive decay, or compound interest. The solution involving the natural logarithm reflects the inherent exponential nature of these phenomena.
-
Probability and Statistics: This type of integral often appears in probability density functions, particularly those involving exponential distributions. Understanding its solution is essential for calculating probabilities and statistical measures.
-
Physics and Engineering: Many physical processes, from the cooling of an object to the discharge of a capacitor, involve exponential relationships and thus integrals of this form.
Frequently Asked Questions (FAQ)
-
Q: Why is the constant of integration 'C' added?
A: The derivative of a constant is always zero. Therefore, adding a constant 'C' to the solution doesn't change its derivative. The constant accounts for the infinite number of functions that can have the same derivative. Different values of 'C' represent different functions with the same derivative.
-
Q: What if the denominator were different? For example, ∫ 1/(1 + 3x) dx?
A: The same u-substitution method applies. You would let u = 1 + 3x, then du = 3dx, leading to:
(1/3) ∫ (1/u) du = (1/3) ln|1 + 3x| + C
-
Q: Can this integral be solved using other methods?
A: While u-substitution is the most efficient approach, it's theoretically possible (though less practical) to use more advanced techniques such as integration by parts or expanding the integrand into a power series. However, these methods would be considerably more complex for this specific integral.
-
Q: What if the integral was ∫ x/(1+2x) dx?
A: This would require a slightly different approach, likely involving polynomial long division or a more sophisticated form of u-substitution to separate the integrand into manageable parts before integration.
Conclusion: Mastering Integration Through Practice
The integral of 1/(1+2x) dx, while initially appearing challenging, becomes manageable with a methodical application of u-substitution. This seemingly simple problem serves as a stepping stone to understanding more complex integration techniques. Mastering integration requires consistent practice and a deep understanding of the underlying mathematical principles. By actively engaging with these concepts and tackling diverse integration problems, you'll build a solid foundation for further explorations in calculus and its numerous applications in science, engineering, and beyond. Remember to always practice and work through various examples to solidify your understanding. The more you practice, the more confident and proficient you'll become in tackling even the most intricate integrals.
Latest Posts
Latest Posts
-
Study Of Sound Mechanical Waves
Sep 15, 2025
-
Rectangular Prism With 5 Cubes
Sep 15, 2025
-
How To Find Work Function
Sep 15, 2025
-
What Is 15 Of 360
Sep 15, 2025
-
Acetic Acid React With Ammonia
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 1 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.